问题描述:


样例:
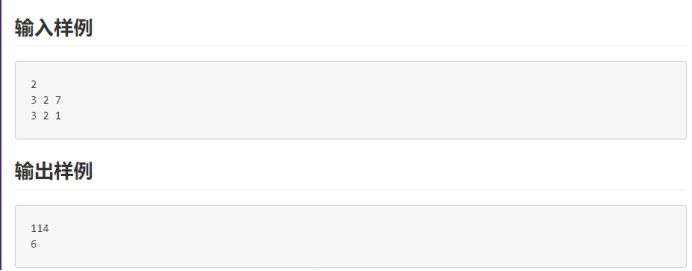
实现解释:
这里等比数列求和使用到的知识点包括:分治和快速幂
其中分治的方法和快速幂的方法是从博客中学习到的:
等比数列分治求和:https://blog.csdn.net/qq_35937273/article/details/82750298
快速幂方法:https://www.cnblogs.com/lca1826/p/6748372.html
结合到本题目中可参考完整代码。
在分治求和和快速幂之外取模操作的实现解释如下:
根据描述可知最后的值是很大的,所以需要取余,但实际上在计算的过程中就需要进行取余操作了。所以需要对快速幂函数和分治函数进行一下处理:
首先操作的基础公式(取余的等价式):
(a + b) % p = (a % p + b % p) % p (1)
(a - b) % p = (a % p - b % p + p) % p (2)
(a * b) % p = (a % p * b % p) % p (3)
a ^ b % p = ((a % p)^b) % p (4)
基于(4)首先需要对快速幂的乘数进行取模处理,然后在乘起来每一个值之前还需要对result进行取模处理,然后还需要对乘起来的值进行取模。这样才能保证快速幂得到的值得到了正常的取模处理(之前就是这里出错所以测试点只过了一个)
基于(1)和(3)需要对分治求和的返回结果分别进行取模处理。
坑点:
取余出现负数:数据超出了范围,是没正确取余导致的,因为正数取余不会得到负数。
完整代码:
#include<iostream>
using namespace std;
long long MOD = 987654323;
long long quickPow(long long q,long long cnt)
{
long long mq = q%MOD;
long long result = 1;
while(cnt!=0)
{
if(cnt&1!=0)
{
result*=mq;
result%=MOD;
}
mq*=mq;
mq%=MOD;
// if(cnt&1!=0)
// {
// result*=mq;
// }
// mq*=mq;
cnt>>=1;
}
return result%MOD;
}
long long getSum(long long q,long long cnt)
{
if(cnt == 0)
return 1;
if(cnt&1!=0)//奇数
{
long long coef = 1+quickPow(q,(cnt+1)/2);
return ((coef%MOD)*getSum(q,(cnt-1)/2))%MOD;
}
else//偶数
{
long long coef = 1+quickPow(q,cnt/2);
return ((((coef%MOD)*getSum(q,cnt/2-1))%MOD)+quickPow(q,cnt))%MOD;
}
}
int main()
{
long long cnt;
cin >> cnt;
long long n,a,q;
while(cnt--)
{
cin >> n >> a >> q;
cout << ((a%MOD)*getSum(q,n-1))%MOD << endl;
}
return 0;
}