暴力
其实这题的暴力就是个模拟。暴力扫一遍 (conn(s_1, n_1)),若出现了 (res) 个 (s_2)。
答案就是 (lfloor res / n1 floor)。
时间复杂度 (O(T(|s_1|n1)))。
算法1:考虑匹配一个 s1 所需的最小字符数
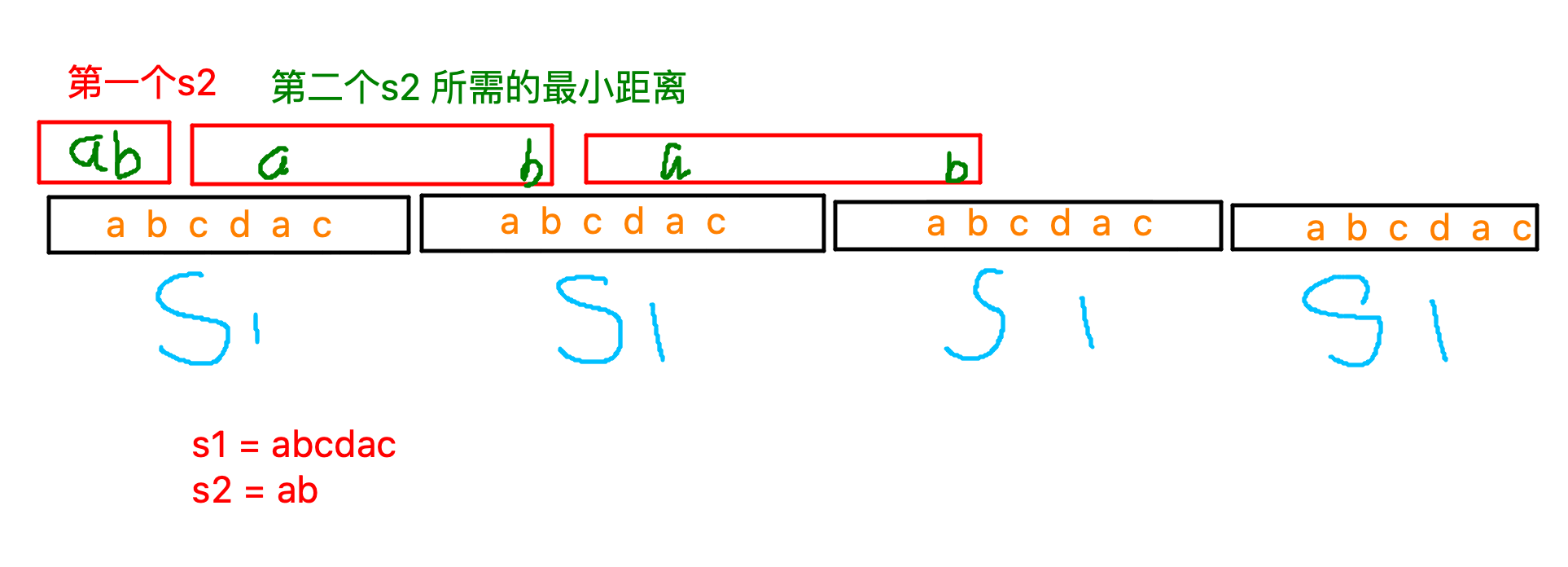
考虑字符串是一直循环的,每走完一个 (s_2),他会从一个位置重新开始匹配。我们考虑预处理出对于从 (0) ~ (|s1|- 1) 这个下标 (i) 开始,匹配一个 (s_2) 所需最小的字符数,设其为 (f[i])。
那么我们就不需要把整个 (conn(s_1, n_1)) 搞出来了,可以搞一个变量 (p = 0) 表示当前走过的字符数,设出现的 (s2) 个数 (res = 0),循环执行:
如果 (p + f[p \% |s1|] <= n1 *|s1|),就 (p += f[p \% |s1|], ans++)。形象理解就是如果还能匹配一个 (s2),并且不超过限制,我就再过一个 (s_2),知道上述条件不符合时停止。
考虑最坏时答案是 (|s_1| * n1 / |s2|)。
所以 时间复杂度 (O(T(|s_1| * n1 / |s2|)))。最坏情况下和暴力一样的,想了那么久你 tm 跟暴力还一样。。
倍增
刚才的跳的过程可以描述为:
- 能跳就跳
- 对于每个 (p) ,有唯一的后继 (p + f[p \% |s1|])
这不就是明显的可以倍增优化吗?
设 (dp[i][j]) 为(s_1)循环节从下标 (i) 出发,匹配 (2 ^ j) 个 (s_2) 串所需的最小字符数。
初始状态:(dp[i][0] = f[i])
状态转移:(dp[i][j] = dp[i][j - 1] + dp[(i + dp[i][j - 1]) \% |s_1|][j - 1]),就是用两个 (2 ^{j - 1}) 拼出 (2 ^ j)。
跳的时候就用倍增模板就行了:
初始设 (p = 0, res = 0),从大到小枚举 (j):
- 如果 (p + f[p \% |s_1|][j] <= n_1 *|s_1|),就 (p += f[p \% |s_1|][j], ans += 2 ^ j)。
时间复杂度
在理论最坏情况下,貌似预处理是 (O(|s| ^ 3)) 的,因为没说只有小写字母,所以考虑构造如下数据:
abcdefghijklmnopqrstuvwxyz......(连续不一样的100个字符)
......zyxwvutsrqponmlkjihgfedcba
那么从 (a),第一个 (s2) 的最后才匹配到第二个字符,要匹配 (|s_1| * |s_2| - |s_2| + 1) 个字符才行
从 (b) 字符出发,要匹配 (|s_1| * |s_2| - |s_2| + 0) 个字符才行
...
这样,对于每个 (i in [0, |s_1|)),他会循环 $ (|s_1| - 1) * |s_2| + 2 - i$。总的就是 (s_1 * ((|s_1|) * |s_2| + 2) - frac{|s_1| - 1 * |s_1|}{2})
(O(T(|s_1| ^ 2|s_2| + log_{|s_1| * n_1 / |s_2|})))。大概最坏情况 (O(1000000T)) 左右。
跑的已经很快了 (13ms)
(Tips:)此题输入比较毒瘤,建议用 (cin)。因为如果用 (scanf) 貌似最后有个换行如果用 ( ot= EOF) 会再算一组数据...
或者可以采取一种奇妙的方式,(scanf()) 这个玩意会返回成功读入变量的数量,你可以判断是否读满了四个变量...
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 105;
char s1[N], s2[N];
int n1, n2, len1, len2, L, f[N][27];
int main() {
while(scanf("%s %d
%s %d", s2, &n2, s1, &n1) == 4) {
memset(f, 0, sizeof f);
len1 = strlen(s1), len2 = strlen(s2), L = log2(len1 * n1 / len2);
for (int i = 0; i < len1; i++)
for (int j = 0; f[i][0] <= len1 * len2 && j < len2; f[i][0]++)
if(s2[j] == s1[(i + f[i][0]) % len1]) j++;
if (f[0][0] > len1 * len2) { puts("0"); continue; }
for (int j = 1; j <= L; j++)
for (int i = 0; i < len1; i++)
f[i][j] = f[i][j - 1] + f[(i + f[i][j - 1]) % len1][j - 1];
int p = 0, ans = 0;
for (int i = L; i >= 0; i--)
if(p + f[p % len1][i] <= len1 * n1) p += f[p % len1][i], ans += 1 << i;
printf("%d
", ans / n2);
}
return 0;
}
算法2 考虑经过一个 s2 匹配的 s1 字符数
字符串匹配这个东西很玄妙,重新阅读这句话:
考虑字符串是一直循环的,每走完一个 (s_2),他会从一个位置重新开始匹配。
那么,我们考虑预处理:
- (f[i]) 为已经匹配到 (s_2) 的第 (i) 位,再走完一个 (s_1),能新匹配 (s_2) 的字符数。
显然,这个东西我们也可以用倍增优化:
设 (dp[i][j]) 为已经匹配到 (s_2) 的第 (i) 位,再走完 (2 ^ j) 个 (s_1),能新匹配 (s_2) 的字符数。
初始状态:(dp[i][0] = f[i])
状态转移:(dp[i][j] = dp[i][j - 1] + dp[(i + dp[i][j - 1]) \% |s_2|][j - 1]),就是用两个 (2 ^{j - 1}) 的(s_2)拼出 (2 ^ j)。
最终的答案求解,只需维护一个指针 (p),枚举 $n_1 $的对应二进制位 (i),如果为 (1),就对应跳 $f[p % |s2|][i] $ 步即可。
时间复杂度
(O(|s_1| * |s_2| + log_2n_1)) 跑的飞快 (3ms)
即使字符串长度出到 $ <= 1000$ ,(n_1, n_2) 到 (long long) 范围也能解决。
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 105;
char s1[N], s2[N];
int n1, n2, len1, len2, L, f[N][20];
int main() {
while(scanf("%s %d
%s %d", s2, &n2, s1, &n1) == 4) {
memset(f, 0, sizeof f);
len1 = strlen(s1), len2 = strlen(s2), L = log2(n1);
for (int i = 0; i < len2; i++)
for (int j = 0; j < len1; j++)
if(s2[(i + f[i][0]) % len2] == s1[j]) f[i][0]++;
if (!f[0][0]) { puts("0"); continue; }
for (int j = 1; j <= L; j++)
for (int i = 0; i < len2; i++)
f[i][j] = f[i][j - 1] + f[(i + f[i][j - 1]) % len2][j - 1];
int p = 0, ans = 0;
for (int i = L; i >= 0; i--)
if(n1 >> i & 1) ans += f[p % len2][i], p += f[p % len2][i];
printf("%d
", ans / len2 / n2);
}
return 0;
}
总结:
-
算法 (1) 的步长是我们的答案,倍增(dp)数组的具体数值是限制我们的字符,我们不知道步长,但我们知道限制。
-
算法 2 的步长是我们已知的 (n_1) 个字符串,倍增数组的具体数值是我们的答案(匹配了多少个字符),我们知道步长,按位枚举 (n_1) 下的二进制串即可。
-
两个东西是互逆的,但是反过来,时间复杂度却有神一般的提升,比较有趣。