论文链接:http://rpg.ifi.uzh.ch/docs/ICRA14_Forster.pdf
论文提出了一种半直接单目视觉里程计,在精确性、鲁棒性和速度方面都有较大的优势。将基于特征的方法(包括追踪特征点和关键帧选择)和基于图像强度的直接法进行结合。
INTRODUCTION介绍了一些基于视觉的运动估计(前端)方法,主要包括基于特征的方法和直接法。特征方法在连续帧中使用描述子进行匹配后采用对极几何进行求解,最后最小化重投影误差优化位姿。该方法太依赖于特征点提取和匹配的准确度,而大多数特征点都为了速度进行优化,而精度则不够高,容易导致误匹配,因此位姿估计易出现漂移。而直接法利用图像强度的变化,最小化光度误差,使用了图像中的所有信息,即使特征点较少或图像模糊结果仍然较好。同时也节省了特征检测和描述子计算的过程。
本文结合了特征点法和直接法,只在选择关键帧时采用特征点法初始化3D点,一旦相机初始位置确定,直接法估计位姿时采用关键点周围的小方块进行追踪。在关键点使用深度滤波器更新,当深度收敛时才将该点加入地图中。

system overview中采用了两个线程:运动估计和地图。运动估计中,采用半直接法:第一步估计出$I_k$和$I_{k-1}$这两帧图像之间的相对位姿,即最小化两帧中相同3D点对应的像素点之间的光度误差。如下图所示:(红色为优化的变量,蓝色的为优化代价)
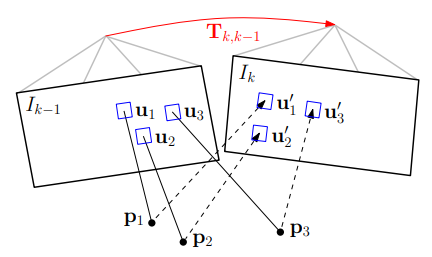
第二步:由于3D点和相机位姿的误差,在进行一次优化,即最小化之前的关键帧$r_i$和当前帧的每个块的光度误差,这次优化的是当前帧的2d位置,如下图所示:
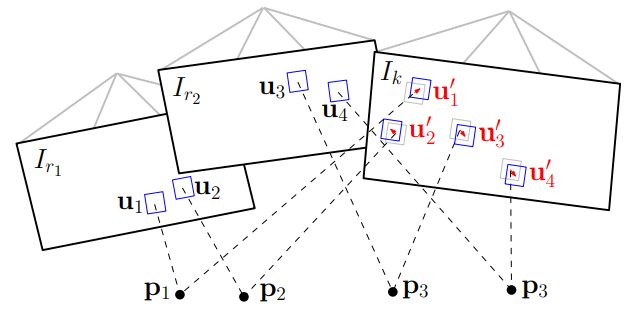
最后一步同时优化位姿和三维空间点,通过最小化重投影误差,该误差利用了第二步中的结果,如下图所示:
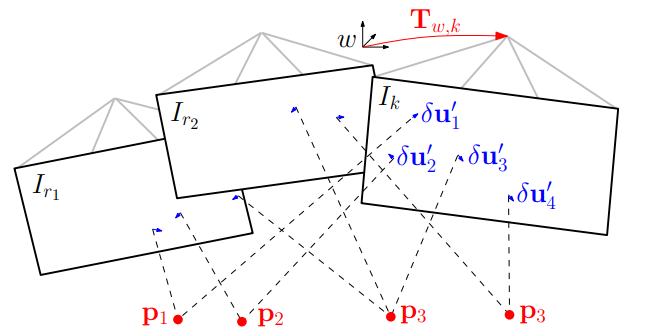
在地图线程中,对于每个2D特征都初始化一个深度滤波器,估计其3d点的深度,当新的关键帧创建时进行初始化,在其他帧进入时更使用贝叶斯滤波新该滤波器,当深度收敛时将该3D点加入地图中。
Notation部分主要是涉及到一些字符公式,定义了一些集合包括二维像素平面和三维点集合等。3D点到像素平面,定义了重投影函数(公式1),这里应该只需要相机内参,以及其逆函数(公式2),采用李代数求解位姿,得到公式3。
MOTION ESTIMATION中运动估计三个步骤的详细说明
A.稀疏点运动模型图像对齐 即系统概述中的第一步
公式4中最小化连续两帧之间的光度误差,其中光度误差可由公式5求出:前一帧的深度已知,将前一帧的像素点和深度通过2d->3d变换(公式2)到3d点,将该3d点通过T(T为当前优化变量)变换到当前帧下,再通过3d->2d变换(公式1)到2d点,即当前帧的像素位置,得到其光度值,与上一帧的像素点求误差。
为了简单起见,假设强度残差为单位方差的正态分布,则可以转化为最小二乘问题。我们只知道稀疏特征点处的深度,但是前文提到采用块匹配,因此使用稀疏特征点的深度替代,进而求出所有块的最小光度误差,见公式7。但公式7不是线性的,因此使用高斯牛顿法,此处还参考了文献27的方法,下次等有时间再研究QAQ。得到光度误差公式8,并对要求的相对位姿进行更新(公式9)。在位姿为0处对其进行泰勒展开,使用高斯牛顿法求解,具体见公式10-12,求出的雅克比矩阵和十四讲中类似,由于是采用块匹配,块的大小为4*4,雅克比矩阵的维度为16*6。由于第k-1帧的光度以及三维点未变,因此可以预先求出雅克比矩阵,实现加速。
B.特征对齐 即系统概述中的第2步
在上一步中,假设求出了第k帧时的三维点,但由于上一帧的深度可能不准,变换的该三维点可能存在误差,加上相机的位姿误差,因此为了进行优化,将相机位姿与地图(前几帧)进行一次对齐,而不是与上一帧对齐。具体做法:将地图中已有的3D点投影到当前帧和前几帧上(每一帧的位姿第一步求出来了),通过所有块的最小化光度误差优化3D点在当前帧的投影,使用Lucas光流法。这里采用仿射变换:一方面因为这一步的块更大(8*8),另一方面相隔的帧数可能比较多。
C.位姿和结构优化
通过第二步我们得到了图像特征之间的对应关系,由于采用的是仿射变换,因此产生了像素误差,怎么理解呢?其实就是图像变换之后不对齐了。因此再做一个最小化投影误差,见公式17。这里还可以做个局部BA对三维点和位姿都进行优化,但实际算法省去了。
D.讨论
上一节的A和C都是优化相机的位姿,冗余么?其实可以直接从第二步,使用lucas光流法实现跟踪,但这样花的时间长,且准确度不够,svo只只需要优化相机的位姿共6个参数,第一步操作满足对极集合限制,确保没有外点。而只使用第一步则会产生较大的漂移。
MAPPING
已知图像以及其位姿,通过估计其深度可以得到3D点,深度估计采用概率分布模型,通过当前图像和相关帧之间的三角化可以计算深度,在极线上进行搜索,相关性最大的块的深度作为3d点深度,当深度收敛时,插入3D点。注意,我们只在关键帧上设定深度滤波器,也就是只求关键帧上关键点的深度。深度初始化为高斯均匀分布,范围为$[d_{min},d_{max}]$。公式见原文,参考了文献[28]和[29]。熟练过程中只需要相机小的运动就能减少深度的不确定性,与仅仅三角化相比,大大减少了外点的数目,因此可以用在具有高度相似的环境中,也可用于稠密建图。
实现细节
- 初始化时,根据前两帧图像,假设它们在同意平面上,求出单应矩阵,初始地图从前两帧中进行重投影
- 为了处理相机存在较大的移动,采用图像金字塔,降采样一半为五层,从最粗糙层开始,每一层上进行误差优化直到收敛,下一层的结果作为上一层的初始化,为了节省时间,在第三层收敛了就不进行了。
- 地图中关键帧的数量保持一定,用于特征匹配和结构优化,确定关键帧的方式之一:新的帧深度超过之前的关键帧的平均深度12%,关键帧满了后删除时间最久远的关键帧。
- 在地图线程中,将图像分为固定的网格,每个网格30*30个像素,网格中初始化一个新的深度滤波器,除非已经找到对应的地图点。该网格也用于重投影。
实验
数据集是在无人机上的俯视相机中采的。再准确率、运行时间和鲁棒性上进行了分析。
时间上快是因为在位姿估计时没有使用特征匹配,在svo中使用了更好的特征,因为深度滤波器的存在,使得特征的追踪变得可靠。深度滤波器也使得鲁棒性更强。
结论
由于使用直接法不用特征匹配,速度快,因此适用于无人机。高速的运动估计和概率方法滤除外点,使得在小场景、重复、高速率环境表现较好。