用R进行统计学分析

1、基本统计

summary函数:R中的summary函数根据输入的类提供输入的摘要。该函数根据输入对象的类调用各种函数。返回值也取决于输入对象。例如，如果输入是一个由数字数据组成的向量，它将为数据提供平均值、中值、最小值、最大值和四分位数，而如果输入是表格(数字)数据，它将为每一列提供类似的计算。

cov:用来计算相关性，通过为函数中的方法参数指定apt值，我们可以计算不同类型的相关系数，即Pearson、Spearman、Kendall等。

data(iris)
summary(iris) 
mean(iris[,1]) 
sd(iris[,1])
cor(iris[,1],iris[,2])    #两个向量之间的相关性
cor(iris[,1],iris[,3])
Cov.mat <- cov(iris[,1:4])
View(Cov.mat)

 

2、缺失值处理

对于大多数这些函数，我们有可能使用na.rm参数。这使用户能够处理丢失的数据。如果我们的数据中缺少值(在R中称为NA)，我们可以设置na.rm参数为真，计算只基于非na值。

a <- c(1:4, NA, 6)
mean(a) # returns NA，R不知道如何处理缺失值NA
mean(a, na.rm=TRUE)  #3.2

 3、 generate probability distributions

n.data <- rnorm(100, 1, 0.1)
hist(n.data)
plot(density(n.data))

 

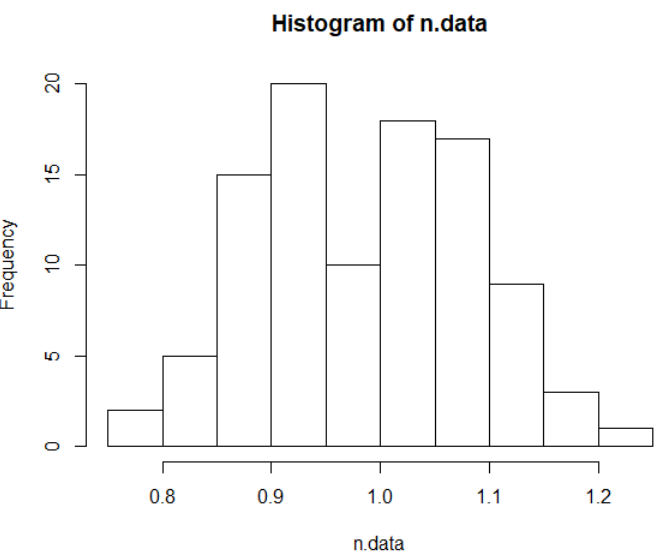
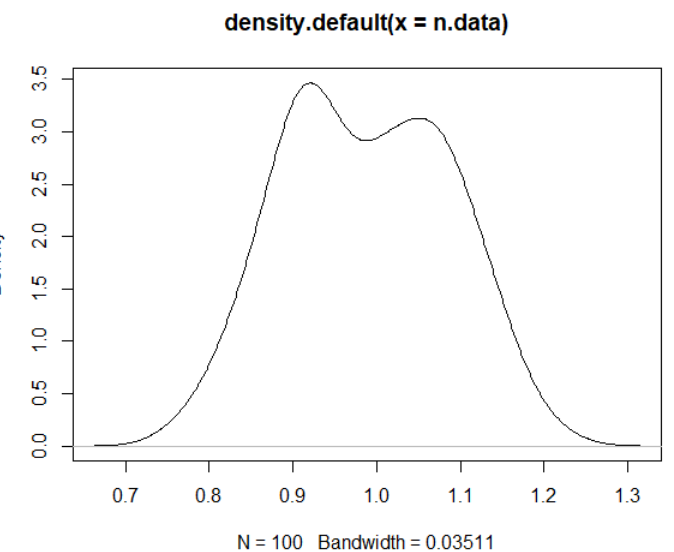
4、统计检验

进行统计检验是为了评估研究或应用结果的重要性，并协助作出定量决定。这个想法是为了确定是否有足够的证据来拒绝对结果的推测。R中的内置函数允许对数据进行多次这样的测试。测试的选择取决于数据和被问到的问题。举例说明，当我们需要将一个组与一个假设值进行比较，并且我们的测量值遵循高斯分布时，我们可以使用一个样本t检验。然而，如果我们有两个组(两个测量值都遵循高斯分布)进行比较，我们可以使用双尾t检验。R有内置的函数来进行这样的测试。

4.1、t-test

t检验(在我们的例子中，它是两个样本t检验)计算的是统计的均值结果偏离实际均值的程度。这里，我们使用R中已经存在的睡眠数据。这些睡眠数据显示了两种药物在增加睡眠时间方面的效果，与10名对照组患者的睡眠数据相比。结果是一个包含9个元素的列表，如p值、置信区间、方法和平均值估计

data(sleep)
test <- t.test(sleep[,1]~sleep[,2])

 4.2、卡方检验

cont <- matrix(c(14, 33, 7, 3), ncol = 2)
colnames(cont) <- c("Sedan", "Convertible")
rownames(cont) <- c("Male", "Female")
test <- chisq.test(as.table(cont))

 4.3、Wilcoxon signed-rank test

x <- c(1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 3.06, 1.30)
y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29)
test <- wilcox.test(x, y, paired = TRUE, alternative = "greater")
str(test)
test$p.value