数据清洗是数据分析的必备环节,在进行分析过程中,会有很多不符合分析要求的数据,例如重复、错误、缺失、异常类数据。
一、 重复值处理
数据录入过程、数据整合过程都可能会产生重复数据,直接删除是重复数据处理的主要方法。pandas提供查看、处理重复数据的方法duplicated和drop_duplicates。以如下数据为例:
>sample = pd.DataFrame({'id':[1,1,1,3,4,5],
'name':['Bob','Bob','Mark','Miki','Sully','Rose'],
'score':[99,99,87,77,77,np.nan],
'group':[1,1,1,2,1,2],})
>sample
group id name score
0 1 1 Bob 99.0
1 1 1 Bob 99.0
2 1 1 Mark 87.0
3 2 3 Miki 77.0
4 1 4 Sully 77.0
5 2 5 Rose NaN
发现重复数据通过duplicated方法完成,如下所示,可以通过该方法查看重复的数据。
>sample[sample.duplicated()]
group id name score
1 1 1 Bob 99.0
需要去重时,可drop_duplicates方法完成:
#Python学习交流群:778463939
>sample.drop_duplicates()
group id name score
0 1 1 Bob 99.0
2 1 1 Mark 87.0
3 2 3 Miki 77.0
4 1 4 Sully 77.0
5 2 5 Rose NaN
drop_duplicates方法还可以按照某列去重,例如去除id列重复的所有记录:
>sample.drop_duplicates('id')
group id name score
0 1 1 Bob 99.0
3 2 3 Miki 77.0
4 1 4 Sully 77.0
5 2 5 Rose NaN
二、 缺失值处理
缺失值是数据清洗中比较常见的问题,缺失值一般由NA表示,在处理缺失值时要遵循一定的原则。
首先,需要根据业务理解处理缺失值,弄清楚缺失值产生的原因是故意缺失还是随机缺失,再通过一些业务经验进行填补。一般来说当缺失值少于20%时,连续变量可以使用均值或中位数填补;分类变量不需要填补,单算一类即可,或者也可以用众数填补分类变量。
当缺失值处于20%-80%之间时,填补方法同上。另外每个有缺失值的变量可以生成一个指示哑变量,参与后续的建模。当缺失值多于80%时,每个有缺失值的变量生成一个指示哑变量,参与后续的建模,不使用原始变量。
在下图中展示了中位数填补缺失值和缺失值指示变量的生成过程。
缺失值填补示例
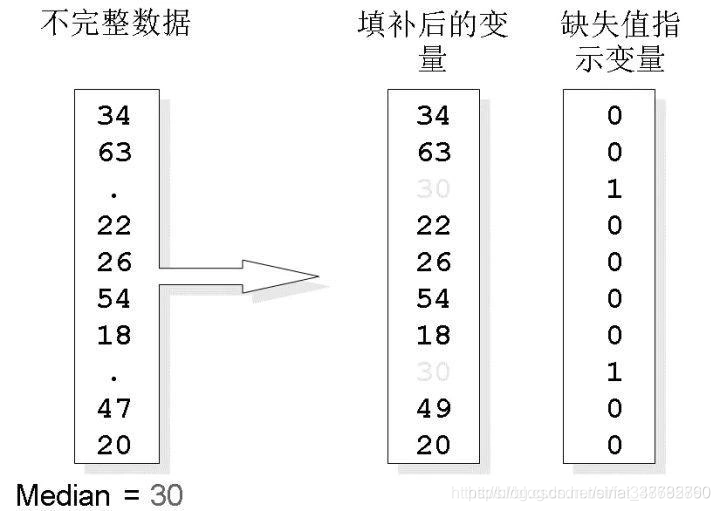
Pandas提供了fillna方法用于替换缺失值数据,其功能类似于之前的replace方法,例如对于如下数据:
> sample
group id name score
0 1.0 1.0 Bob 99.0
1 1.0 1.0 Bob NaN
2 NaN 1.0 Mark 87.0
3 2.0 3.0 Miki 77.0
4 1.0 4.0 Sully 77.0
5 NaN NaN NaN NaN
分步骤进行缺失值的查看和填补如下:
1. 查看缺失情况
在进行数据分析前,一般需要了解数据的缺失情况,在Python中可以构造一个lambda函数来查看缺失值,该lambda函数中,sum(col.isnull())表示当前列有多少缺失,col.size表示当前列总共多少行数据:
>sample.apply(lambda col:sum(col.isnull())/col.size)
group 0.333333
id 0.166667
name 0.166667
score 0.333333
dtype: float64
2. 以指定值填补
pandas数据框提供了fillna方法完成对缺失值的填补,例如对sample表的列score填补缺失值,填补方法为均值:
>sample.score.fillna(sample.score.mean())
0 99.0
1 85.0
2 87.0
3 77.0
4 77.0
5 85.0
Name: score, dtype: float64
当然还可以以分位数等方法进行填补:
>sample.score.fillna(sample.score.median())
0 99.0
1 82.0
2 87.0
3 77.0
4 77.0
5 82.0
Name: score, dtype: float64
3. 缺失值指示变量
pandas数据框对象可以直接调用方法isnull产生缺失值指示变量,例如产生score变量的缺失值指示变量:
>sample.score.isnull()
0 False
1 True
2 False
3 False
4 False
5 True
Name: score, dtype: bool
若想转换为数值0,1型指示变量,可以使用apply方法,int表示将该列替换为int类型。
>sample.score.isnull().apply(int)
0 0
1 1
2 0
3 0
4 0
5 1
Name: score, dtype: int64
三、噪声值处理
噪声值指数据中有一个或几个数值与其他数值相比差异较大,又称为异常值、离群值(outlier)。
对于大部分的模型而言,噪声值会严重干扰模型的结果,并且使结论不真实或偏颇。需要在数据预处理的时候清除所以噪声值。噪声值的处理方法很多,对于单变量,常见的方法有盖帽法、分箱法;多变量的处理方法为聚类法。下面进行详细介绍:
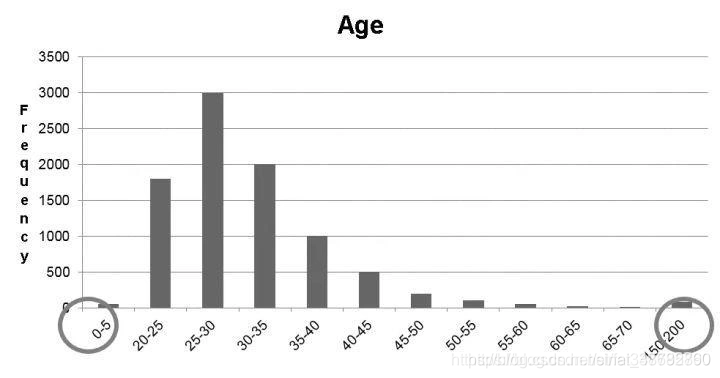
1. 盖帽法
盖帽法将某连续变量均值上下三倍标准差范围外的记录替换为均值上下三倍标准差值,即盖帽处理
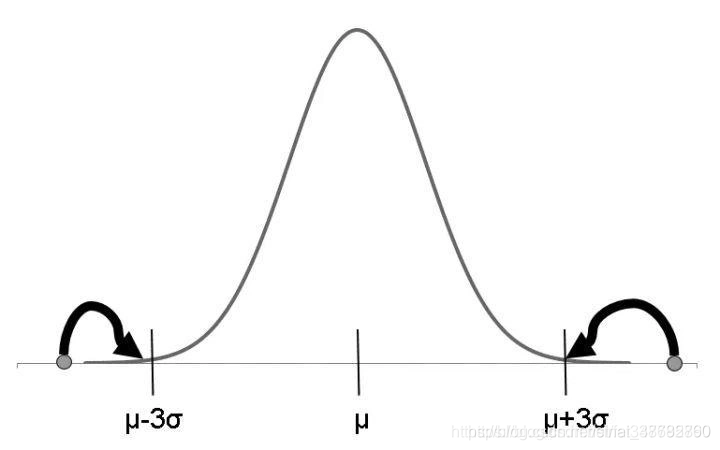
Python中可自定义函数完成盖帽法。如下所示,参数x表示一个pd.Series列,quantile指盖帽的范围区间,默认凡小于百分之1分位数和大于百分之99分位数的值将会被百分之1分位数和百分之99分位数替代:
#Python学习交流群:778463939
>def cap(x,quantile=[0.01,0.99]):
"""盖帽法处理异常值
Args:
x:pd.Series列,连续变量
quantile:指定盖帽法的上下分位数范围
"""
# 生成分位数
Q01,Q99=x.quantile(quantile).values.tolist()
# 替换异常值为指定的分位数
if Q01 > x.min():
x = x.copy()
x.loc[x<Q01] = Q01
if Q99 < x.max():
x = x.copy()
x.loc[x>Q99] = Q99
return(x)
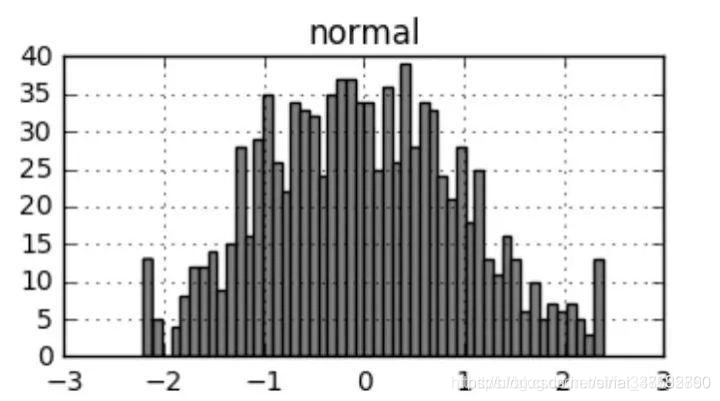
现生成一组服从正态分布的随机数,sample.hist表示产生直方图,更多绘图方法会在下一章节进行讲解:
>sample = pd.DataFrame({'normal':np.random.randn(1000)})
>sample.hist(bins=50)
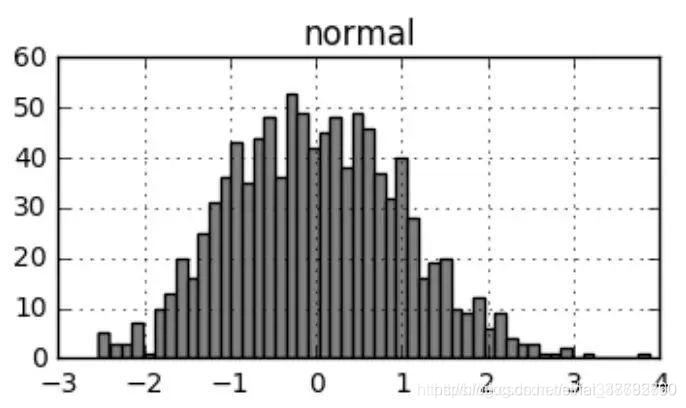
对pandas数据框所有列进行盖帽法转换,可以以如下写法,从直方图对比可以看出盖帽后极端值频数的变化。
>new = sample.apply(cap,quantile=[0.01,0.99])
>new.hist(bins=50)
2. 分箱法
分箱法通过考察数据的“近邻”来光滑有序数据的值。有序值分布到一些桶或箱中。
分箱法包括等深分箱:每个分箱中的样本量一致;等宽分箱:每个分箱中的取值范围一致。直方图其实首先对数据进行了等宽分箱,再计算频数画图。
比如价格排序后数据为:4、8、15、21、21、24、25、28、34
将其划分为(等深)箱:
-
箱1:4、8、15
-
箱2:21、21、24
-
箱3:25、28、34
将其划分为(等宽)箱:
-
箱1:4、8
-
箱2:15、21、21、24
-
箱3:25、28、34
分箱法将异常数据包含在了箱子中,在进行建模的时候,不直接进行到模型中,因而可以达到处理异常值的目的。
pandas的qcut函数提供了分箱的实现方法,下面介绍如何具体实现。
等宽分箱:qcut函数可以直接进行等宽分箱,此时需要的待分箱的列和分箱个数两个参数,如下所示,sample数据的int列为从10个服从标准正态分布的随机数:
>sample =pd.DataFrame({'normal':np.random.randn(10)})
>sample
normal
0 0.065108
1 -0.597031
2 0.635432
3 -0.491930
4 -1.894007
5 1.623684
6 1.723711
7 -0.225949
8 -0.213685
9 -0.309789
现分为5箱,可以看到,结果是按照宽度分为5份,下限中,cut函数自动选择小于列最小值一个数值作为下限,最大值为上限,等分为五分。结果产生一个Categories类的列,类似于R中的factor,表示分类变量列。
此外弱数据存在缺失,缺失值将在分箱后将继续保持缺失,如下所示:
#Python学习交流群:778463939
>pd.cut(sample.normal,5)
0 (-0.447, 0.277]
1 (-1.17, -0.447]
2 (0.277, 1.0]
3 (-1.17, -0.447]
4 (-1.898, -1.17]
5 (1.0, 1.724]
6 (1.0, 1.724]
7 (-0.447, 0.277]
8 (-0.447, 0.277]
9 (-0.447, 0.277]
Name: normal, dtype: category
Categories (5, interval[float64]): [(-1.898, -1.17] < (-1.17, -0.447] < (-0.447, 0.277] < (0.277, 1.0] < (1.0, 1.724]]
这里也可以使用labels参数指定分箱后各个水平的标签,如下所示,此时相应区间值被标签值替代:
> pd.cut(sample.normal,bins=5,labels=[1,2,3,4,5])
0 1
1 1
2 2
3 2
4 3
5 3
6 4
7 4
8 5
9 5
Name: normal, dtype: category
Categories (5, int64): [1 < 2 < 3 < 4 < 5]
标签除了可以设定为数值,也可以设定为字符,如下所示,将数据等宽分为两箱,标签为‘bad’,‘good’:
>pd.cut(sample.normal,bins=2,labels=['bad','good'])
0 bad
1 bad
2 bad
3 bad
4 bad
5 good
6 good
7 good
8 good
9 good
Name: normal, dtype: category
Categories (2, object): [bad < good]
等深分箱:等深分箱中,各个箱的宽度可能不一,但频数是几乎相等的,所以可以采用数据的分位数来进行分箱。依旧以之前的sample数据为例,现进行等深度分2箱,首先找到2箱的分位数:
>sample.normal.quantile([0,0.5,1])
0.0 0.0
0.5 4.5
1.0 9.0
Name: normal, dtype: float64
在bins参数中设定分位数区间,如下所示完成分箱,include_lowest=True参数表示包含边界最小值包含数据的最小值:
>pd.cut(sample.normal,bins=sample.normal.quantile([0,0.5,1]),
include_lowest=True)
0 [0, 4.5]
1 [0, 4.5]
2 [0, 4.5]
3 [0, 4.5]
4 [0, 4.5]
5 (4.5, 9]
6 (4.5, 9]
7 (4.5, 9]
8 (4.5, 9]
9 (4.5, 9]
Name: normal, dtype: category
Categories (2, object): [[0, 4.5] < (4.5, 9)]
此外也可以加入label参数指定标签,如下所示:
>pd.cut(sample.normal,bins=sample.normal.quantile([0,0.5,1]),
include_lowest=True)
0 bad
1 bad
2 bad
3 bad
4 bad
5 good
6 good
7 good
8 good
9 good
Name: normal, dtype: category
Categories (2, object): [bad < good]
3. 多变量异常值处理-聚类法
通过快速聚类法将数据对象分组成为多个簇,在同一个簇中的对象具有较高的相似度,而不同的簇之间的对象差别较大。聚类分析可以挖掘孤立点以发现噪声数据,因为噪声本身就是孤立点。
本案例考虑两个变量income和age,散点图所示,其中A、B表示异常值:
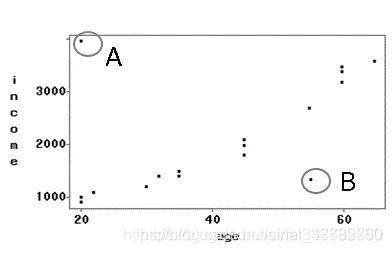
对于聚类方法处理异常值,其步骤如下所示:
-
输入:数据集S(包括N条记录,属性集D:{年龄、收入}),一条记录为一个数据点,一条记录上的每个属性上的值为一个数据单元格。数据集S有N×D个数据单元格,其中某些数据单元格是噪声数据。
-
输出:孤立数据点如图所示。孤立点A是我们认为它是噪声数据,很明显它的噪声属性是收入,通过对收入变量使用盖帽法可以剔除A。
另外,数据点B也是一个噪声数据,但是很难判定它在哪个属性上的数据出现错误。这种情况下只可以使用多变量方法进行处理。
常用检查异常值聚类算法为K-means聚类,会在后续章节中详细介绍,本节不赘述。