属于是提升智力。
AT2043 [AGC004C] AND Grid
考虑把偶数行染红,奇数行染黑,最左列染红,最右列染黑。
AT2386 [AGC016B] Colorful Hats
全局颜色数为\(cnt\),考虑到只有两种答案,那么就是\(cnt - 1\),\(cnt\)。
那么只有三种情况:
若\(\max - \min > 1\),则不存在答案。
\(c\)为\(\min\)出现的次数。
若\(\max = \min\),要么\(c = n - 1\),否则\(2 \times c \leq n\)
若\(\max = \min + 1,\min < c\),要么\(n - c < 2(\max - c)\)
CF1041E Tree Reconstruction
考虑一定有一个块的最大的是\(n\)。
而且考虑如果出现\(k\)次\(a_i\)为和\(n\)之间离她最近的大于\(a_i\),有\(k\)条边。
直接考虑构造一个菊花图即可。
同时在\(n\)和\(a_i\)中只能出现未出现的点。
CF1311E Construct the Binary Tree
考虑先构造出一个链,然后依次调整每次从叶子节点调整到成为另外一个点的儿子,其减少了\(dep_u - dep_v\)的贡献,知每次能减少的贡献是一个连续区间,那么每次贪心的减能减的最大即可。
AT5761 Odd Sum Rectangles
先求出理论上界。
设\(H = 2 ^ x,W = 2 ^ y\)
考虑先枚举列\(\frac{W(W - 1)}{2}\)
然后枚举行,知每次选出前缀和奇偶性不同的即可。
那么有\(\frac{H^2}{2} * \frac{W(W - 1)}{2}\)
接下来可出一种可构造的方法。
AT5761 Odd Sum Rectangles
#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 5;
int n, m;
int a[N][N];
void cons(int l, int r, int x, int y) {
if (l > r || x > y) return;
int mx = (l + r) >> 1, my = (x + y) >> 1;
a[mx][my] = 1;
cons(l, mx - 1, x, my - 1);
cons(mx + 1, r, x, my - 1);
cons(l, mx - 1, my + 1, y);
cons(mx + 1, r, my + 1, y);
}
int main() {
scanf("%d%d", &n, &m);
cons(1, (1 << n) - 1, 1, (1 << m) - 1);
for (int i = 1; i < 1 << n; ++i, puts(""))
for (int j = 1; j < 1 << m; ++j) printf("%d", a[i][j]);
}
AT4850 [ABC164F] I hate Matrix Construction

遇到此类异或或者和的构造问题,记得拆位。
AT4432 [ARC103B] Robot Arms
考虑\(x + y\)的奇偶性相同才有答案。
考虑构造\([1,....,2^k]\),可以构造出\(x + y <= 2^k - 1\)。
考虑每次减少绝对值较大的那个值即可。
AT4378 [AGC027D] Modulo Matrix
构造题真一点都不会呗我日。
考虑黑白染色格。
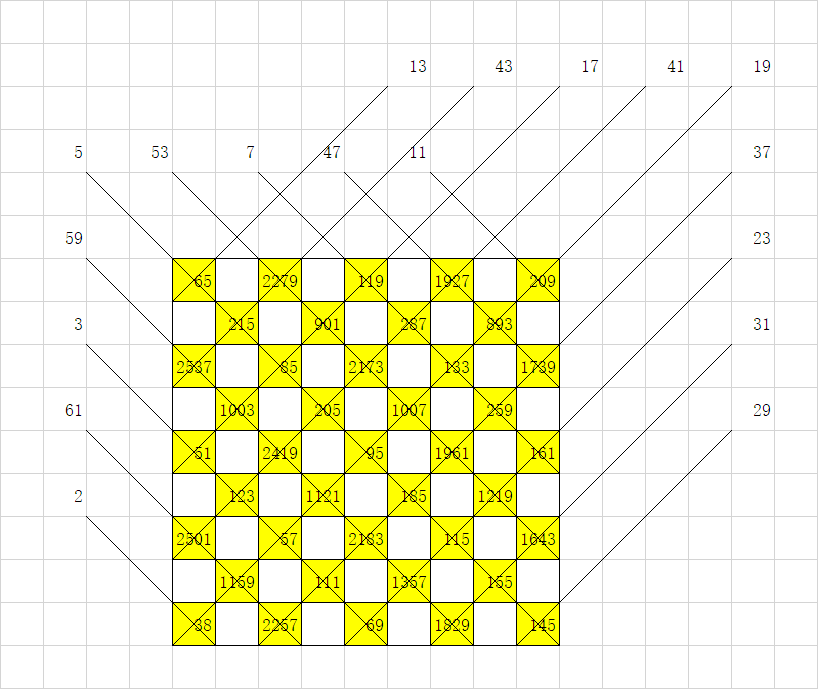
然后在白格上填上四周\(lcm + 1\)。
[ARC102B] All Your Paths are Different Lengths
为数不多的自己做出来的构造了。
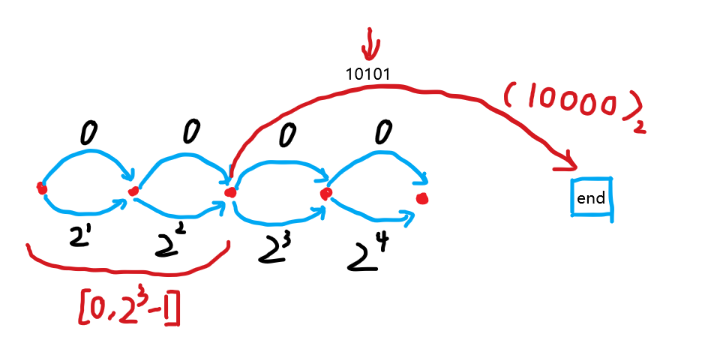
考虑这样一个模型\(i \to i + 1\ with\ (2^i / 0)\)
这样使用了\(2*n\)条边可以让\(1 \to n\)有\(2^{n + 1} - 1\)种权值。
那么考虑小于\(L\)的限制,我们使用数位\(dp\),我们看在哪一位可以任意组合权值,在其后一位往\(end\)连一条前缀权值边即可。
可以看看图。
[AGC025D] Choosing Points
猜想距离为\(\sqrt d\)的点对为二分图,直接黑白染色即可。
证明参照。

AT3877 [ARC089C] GraphXY
考虑设\(f_{i,j} = \max(d_{x,y} - i * x - j*y)\)
考虑对这组\(f_{i,j}\ check\)
如果可以的话,我们拉两条全\(X\)与全\(Y\)的链即可。