我们先放题面——
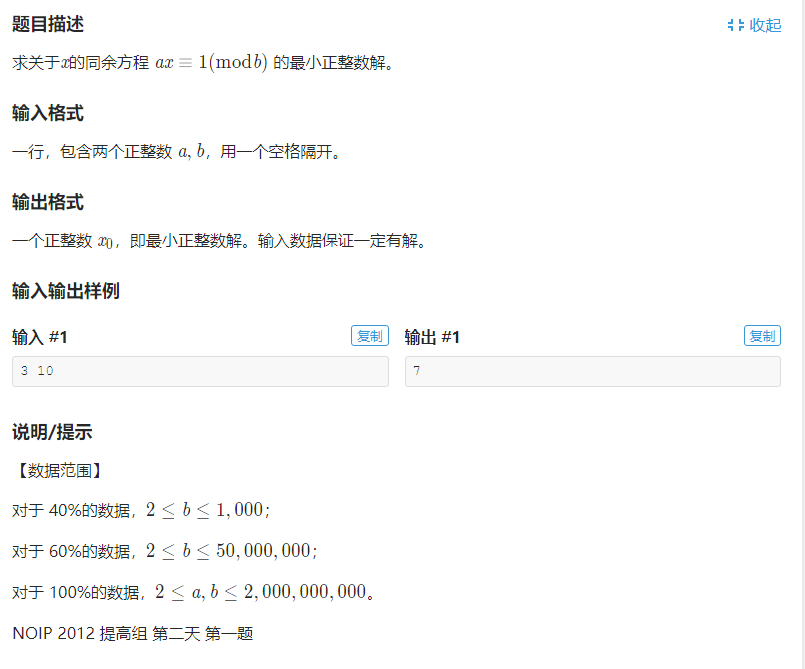
RT就是求一个线性同余方程ax≡1(mod b)的最小正整数解
我们可以将这个同于方程转换成这个方程比较好理解 ax=1+bn(n为整数
我们再进行一个移项变为ax-bn=1 我们设-n为y
那么这个方程就变成了ax+by=1这一个不定方程
我们可以完全可以先解出这一个方程的一个特解x0,y0(解法下面讲)
因为我们求解出的特解有可能会大于我们最后的答案也有可能小于我们最后的答案(为负数)
这个时候我们需要一个性质——
若gcd(a, b) = d,则方程ax ≡ c (mod b)在[0, b/d - 1]上有唯一解。
证明:
该方程等价于ax + by = c,如果有解,两边同除以d,就有a/d * x + b/d * y = c/d,即a/d * x ≡ c/d (mod b/d),显然gcd(a/d, b/d) = 1,所以由一知道x在[0, b/d - 1]上有唯一解。所以ax + by = c的x在[0, b/d - 1]上有唯一解,即ax ≡ c (mod b)在[0, b/d - 1]上有唯一解,得证!
如果得到ax ≡ c (mod b)的某一特解X,那么我令r = b/gcd(a, b),可知x在[0, r-1]上有唯一解,所以x = (X % r + r) % r就可以求出最小非负整数解x了!X % r可能是负值,此时保持在[-(r-1), 0]内,正值则保持在[0, r-1]内。加上r就保持在[1, 2r - 1]内,所以再模一下r就在[0, r-1]内了。
又因为——对于不定方程ax+by=n来说,唯有gcd(a,b)|n时才有答案,又因为对于这题来说n=1,所以gcd(a,b)只能是1(也就是a,b互质)
所以答案就是(x0%b+b)%b;
于是我们只要能求解ax+by=1这个方程的特解就可以了
我们使用扩展欧几里得算法
回忆我们欧几里得算法求gcd的方法
gcd(a,b)=gcd(b,a%b)(b!=0);
a(b==0)
我们通过递归来求。
我们可以使用同样的方法将我们的不定方程 ax+by=gcd(a,b)(本题就是1啦)变为bx+(a%b)y=gcd(b,a%b)=gcd(a,b)
我们将a%b变为a-a/b*b(‘/’为整除答案)
所以也就变为了bx+(a-a/b*b)y=ay+b(x-a/b*y)
所以我们只要解bx+(a%b)y这个方程的解x1,y1就可以得到ax+by的解x=y1,y=x1-a/b*y1
所以我们也可以递归到b=0时 x就等于1 然后一直逆推回答案
假如ax+by!=gcd(a,b)呢(这里已经与本题无关了)
我们设ax+by=c 设gcd(a,b)=d 如果d|c
我们可以通过上面的方法求出a(x*(d/c))+b(y*(d/c))=d的一个特解;
再将特解除以d/c也就是乘c/d
假如d|c不成立的话 那么就没有以上过程 所以当gcd(a,b)不整除c时该不定方程无解
所以我们再回到这道题,我们只要使用扩展欧几里得求ax+by=1的一组特解再用(x0%b+b)%b作为答案就好啦!
贴代码——

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 long long a,b; 6 long long x,y; 7 void exgcd(long long a,long long b) 8 { 9 if(b==0) 10 { 11 x=1; 12 y=0; 13 return ; 14 } 15 else 16 exgcd(b,a%b); 17 long long x1=x; 18 x=y; 19 y=x1-a/b*y; 20 } 21 int main() 22 { 23 scanf("%lld%lld",&a,&b); 24 exgcd(a,b); 25 printf("%lld",(x%b+b)%b); 26 }
(好了,本篇题解就到这里了,慢走)
(有什么不懂可以加qq2733524923我们一起探讨哦)QWQ
