文章作者:yx_th000文章来源:Cherish_yimi (http://www.cnblogs.com/cherish_yimi/)
转载请注明,谢谢合作。
关键词:trie trie树 数据结构
[本文新址:http://www.ahathinking.com/archives/14.html ]
前几天学习了并查集和trie树,这里总结一下trie。
本文讨论一棵最简单的trie树,基于英文26个字母组成的字符串,讨论插入字符串、判断前缀是否存在、查找字符串等基本操作;至于trie树的删除单个节点实在是少见,故在此不做详解。
l Trie原理
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
l Trie性质
好多人说trie的根节点不包含任何字符信息,我所习惯的trie根节点却是包含信息的,而且认为这样也方便,下面说一下它的性质 (基于本文所讨论的简单trie树)
1. 字符的种数决定每个节点的出度,即branch数组(空间换时间思想)
2. branch数组的下标代表字符相对于a的相对位置
3. 采用标记的方法确定是否为字符串。
4. 插入、查找的复杂度均为O(len),len为字符串长度
l Trie的示意图
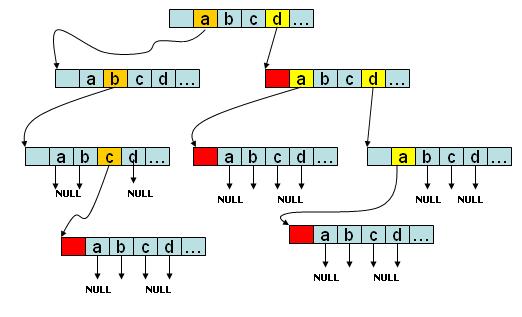
如图所示,该trie树存有abc、d、da、dda四个字符串,如果是字符串会在节点的尾部进行标记。没有后续字符的branch分支指向NULL
l TrieTrie的优点举例
已知n个由小写字母构成的平均长度为10的单词,判断其中是否存在某个串为另一个串的前缀子串。下面对比3种方法:
1. 最容易想到的:即从字符串集中从头往后搜,看每个字符串是否为字符串集中某个字符串的前缀,复杂度为O(n^2)。
2. 使用hash:我们用hash存下所有字符串的所有的前缀子串。建立存有子串hash的复杂度为O(n*len)。查询的复杂度为O(n)* O(1)= O(n)。
3. 使用trie:因为当查询如字符串abc是否为某个字符串的前缀时,显然以b,c,d....等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(n*len),而建立+查询在trie中是可以同时执行的,建立的过程也就可以成为查询的过程,hash就不能实现这个功能。所以总的复杂度为O(n*len),实际查询的复杂度只是O(len)。
解释一下hash为什么不能将建立与查询同时执行,例如有串:911,911456输入,如果要同时执行建立与查询,过程就是查询911,没有,然后存入9、91、911,查询911456,没有然后存入9114、91145、911456,而程序没有记忆功能,并不知道911在输入数据中出现过。所以用hash必须先存入所有子串,然后for循环查询。
而trie树便可以,存入911后,已经记录911为出现的字符串,在存入911456的过程中就能发现而输出答案;倒过来亦可以,先存入911456,在存入911时,当指针指向最后一个1时,程序会发现这个1已经存在,说明911必定是某个字符串的前缀,该思想是我在做pku上的3630中发现的,详见本文配套的“入门练习”。
l Trie的简单实现(插入、查询)
1

2
 #include <iostream>
#include <iostream>3
 using namespace std;
using namespace std;4

5
 const int branchNum = 26; //声明常量
const int branchNum = 26; //声明常量 6
 int i;
int i;7

8
 struct Trie_node
struct Trie_node9
 {
{10
 bool isStr; //记录此处是否构成一个串。
bool isStr; //记录此处是否构成一个串。11
 Trie_node *next[branchNum];//指向各个子树的指针,下标0-25代表26字符
Trie_node *next[branchNum];//指向各个子树的指针,下标0-25代表26字符12
 Trie_node():isStr(false)
Trie_node():isStr(false)13
 {
{14
 memset(next,NULL,sizeof(next));
memset(next,NULL,sizeof(next));15
 }
}16
 };
};17

18
 class Trie
class Trie19
 {
{20
 public:
public:21
 Trie();
Trie();22
 void insert(const char* word);
void insert(const char* word);23
 bool search(char* word);
bool search(char* word); 24
 void deleteTrie(Trie_node *root);
void deleteTrie(Trie_node *root);25
 private:
private:26
 Trie_node* root;
Trie_node* root;27
 };
};28

29
 Trie::Trie()
Trie::Trie()30
 {
{31
 root = new Trie_node();
root = new Trie_node();32
 }
}33

34
 void Trie::insert(const char* word)
void Trie::insert(const char* word)35
 {
{36
 Trie_node *location = root;
Trie_node *location = root;37
 while(*word)
while(*word)38
 {
{39
 if(location->next[*word-'a'] == NULL)//不存在则建立
if(location->next[*word-'a'] == NULL)//不存在则建立40
 {
{41
 Trie_node *tmp = new Trie_node();
Trie_node *tmp = new Trie_node();42
 location->next[*word-'a'] = tmp;
location->next[*word-'a'] = tmp;43
 }
} 44
 location = location->next[*word-'a']; //每插入一步,相当于有一个新串经过,指针要向下移动
location = location->next[*word-'a']; //每插入一步,相当于有一个新串经过,指针要向下移动45
 word++;
word++;46
 }
}47
 location->isStr = true; //到达尾部,标记一个串
location->isStr = true; //到达尾部,标记一个串48
 }
}49

50
 bool Trie::search(char *word)
bool Trie::search(char *word)51
 {
{52
 Trie_node *location = root;
Trie_node *location = root;53
 while(*word && location)
while(*word && location)54
 {
{55
 location = location->next[*word-'a'];
location = location->next[*word-'a'];56
 word++;
word++;57
 }
}58
 return(location!=NULL && location->isStr);
return(location!=NULL && location->isStr);59
 }
}60

61
 void Trie::deleteTrie(Trie_node *root)
void Trie::deleteTrie(Trie_node *root)62
 {
{63
 for(i = 0; i < branchNum; i++)
for(i = 0; i < branchNum; i++)64
 {
{65
 if(root->next[i] != NULL)
if(root->next[i] != NULL)66
 {
{67
 deleteTrie(root->next[i]);
deleteTrie(root->next[i]);68
 }
}69
 }
}70
 delete root;
delete root;71
 }
}72

73
 void main() //简单测试
void main() //简单测试74
 {
{75
 Trie t;
Trie t;76
 t.insert("a");
t.insert("a"); 77
 t.insert("abandon");
t.insert("abandon");78
 char * c = "abandoned";
char * c = "abandoned";79
 t.insert(c);
t.insert(c);80
 t.insert("abashed");
t.insert("abashed");81
 if(t.search("abashed"))
if(t.search("abashed"))82
 printf("true
");
printf("true
");83
 }
}其他相关网页:http://www.nocow.cn/index.php/Trie
http://blog.csdn.net/fancyerii/article/details/7237565