1,基本思想:
1,用一维数组存储顶点:描述顶点相关的数据;
2,用二维数组存储边:描述顶点间的关系和权;
2,邻接矩阵法(二维数组存储权值表示边):
1,设图 A = (V, E) 是一个有 n 个顶点的图,图的邻接矩阵为 Edge[n][n],则:

2,解决工程问题时,习惯于对图中的每个顶点进行编号,当不需要权值时,取 w 非空表示结点间有连接;
3,无向图的邻接矩阵是对称的,有向图的邻接矩阵可能不是对称的;
3,邻接矩阵设计与实现:
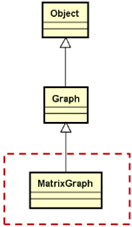
1,如何具体表示顶点集数组?
2,如何具体表示边集数组?
4,实现方式一:直接使用数组表示顶点集和边集:

1,将邻接矩阵直接搬到代码中,这种方法不科学;
2,分析下面代码的效率:
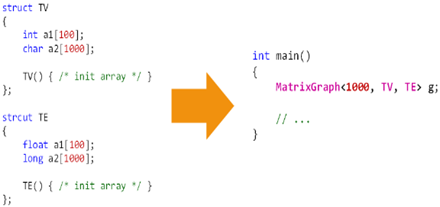
1,构造效率低下:
1,图对象初始化时,频繁调用顶点类型和边类型的构造函数;
2,空间使用率低下:
1,图对象占用大量空间,而大多数空间处于闲置状态;
3,无法表示空值:
1,无法用统一的方式表示边为空的情形;
5,实现方式二:使用指针数组表示顶点集和边集:
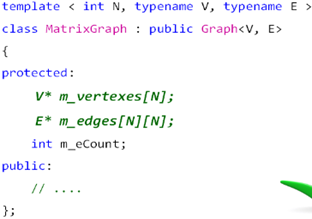
1,构造效率:
1,初始化图对象时,只需要将数组元素赋值为空,不需要调用顶点类型 和边类型的构造函数;
2,空间使用率:
1,顶点数据元素和边数据元素在需要时动态创建;
3,空值的表示:
1,任意的顶点类型和边类型都是用 NULL 表示空值;
6,图的邻接矩阵结构:
1 #ifndef MATRIXGRAPH_H 2 #define MATRIXGRAPH_H 3 4 #include "Graph.h" 5 #include "Exception.h" 6 #include "DynamicArray.h" 7 8 namespace DTLib 9 { 10 11 /* MatirxGraph 无法动态 添加/删除 顶点,图对象空间利用率低。不管顶点是否连接,都会占用空间,使用数组浪费空间,用链表替换数组,将邻接矩阵换为邻接链表法;适用于内存资源富足场合 */ 12 template < int N, typename V, typename E > // N 是图中顶点个数,V 是与顶点相关的数据类型,E 是权值的类型; 13 class MatrixGraph : public Graph<V, E> 14 { 15 protected: 16 V* m_vertexes[N]; // 每个成员都是指向顶点的相关联的数据元素的指针,这里的数据是工程需要、工程相关的背景; 17 E* m_edges[N][N]; // 邻接矩阵 18 int m_eCount; // 当前图中边的个数 19 20 public: 21 MatrixGraph() 22 { 23 for(int i=0; i<vCount(); i++) // 指针数组初始化 24 { 25 m_vertexes[i] = NULL; // 没有一个数据元素和顶点相关联 26 for(int j=0; j<vCount(); j++) 27 { 28 m_edges[i][j] = NULL; // 一条边也没有 29 } 30 } 31 32 m_eCount = 0; 33 } 34 35 /* 获取和顶点 i 相关联的元素的值 */ 36 V getVertex(int i) // O(1) 37 { 38 V ret; 39 40 if( !getVertex(i, ret) ) 41 { 42 THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ..."); 43 } 44 45 return ret; 46 } 47 48 /* 获取顶点 i 所关联的元素值 value */ 49 bool getVertex(int i, V& value) // O(1) 50 { 51 bool ret = ( (0 <= i) && (i < vCount()) ); // i 的合法性 52 53 if( ret ) 54 { 55 if( m_vertexes[i] != NULL ) // 有具体元素关联 56 { 57 value = *(m_vertexes[i]); 58 } 59 else 60 { 61 THROW_EXCEPTION(InvalidOperationException, "No value assigned to this vertex ..."); 62 } 63 } 64 return ret; 65 } 66 67 /* 设置和顶点相关联的元素 */ 68 bool setVertex(int i, const V& value) // O(1) 69 { 70 bool ret = ( (0 <= i) && (i < vCount()) ); 71 72 if( ret ) 73 { 74 V* data = m_vertexes[i]; // 中间数据 data 为了异常安全 75 76 if( data == NULL ) // 没有具体元素关联 77 { 78 data = new V(); 79 } 80 81 if( data != NULL ) // 申请成功 82 { 83 *data = value; // 设置值,单位和要加指针?如果这里发生异常安全,则下面代码不执行,图还是正常的 84 85 m_vertexes[i] = data; 86 } 87 else 88 { 89 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to store new vertex value ..."); 90 } 91 } 92 93 return ret; 94 } 95 96 /* 获取从 i 作为起点的可达的顶点的编号,到数组中 */ 97 SharedPointer< Array<int> > getAdgacent(int i) // O(n) 98 { 99 DynamicArray<int>* ret = NULL; // 定义返回值对象 100 101 if( (0 <= i) && (i < vCount()) ) // i 取值要合法 102 { 103 int n = 0; 104 105 for(int j=0; j<vCount(); j++) // 查找 i 行关联点 106 { 107 if( m_edges[i][j] != NULL ) // 顶点 i 和 j 相关联 108 { 109 n++; // n 表示与 i 相关联的顶点个数 110 } 111 } 112 113 ret = new DynamicArray<int>(n); // 创建返回值对象 114 115 if( ret != NULL ) // 创建成功 116 { 117 for(int j=0, k=0; j<vCount(); j++) // k 作为辅助变量 118 { 119 if( m_edges[i][j] != NULL ) 120 { 121 ret->set(k++, j); // 记录对应的顶点编号到数组对象中 122 } 123 } 124 } 125 else 126 { 127 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object ..."); 128 } 129 } 130 else 131 { 132 THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ..."); 133 } 134 135 return ret; 136 } 137 138 /* 判断 i 到 j 顶点边是否连接,值不为空就连接 */ 139 bool isAdjacent(int i, int j) 140 { 141 return (0 <= i) && (i < vCount()) && (0 <= j) && (j < vCount()) && (m_edges[i][j] != NULL); 142 } 143 144 /* 获取顶点 i 到顶点 j 边上面的权值 */ 145 E getEdge(int i, int j) // O(1) 146 { 147 E ret; 148 149 if( !getEdge(i, j, ret) ) // 直接获得值 150 { 151 THROW_EXCEPTION(InvalidParameterException, "Index <i, j> is invalid ..."); 152 } 153 154 return ret; 155 } 156 157 /* 获取顶点 i 到顶点 j 边上面的权值 */ 158 bool getEdge(int i, int j, E& value) // O(1) 159 { 160 bool ret = ( (0 <= i) && (i < vCount()) && 161 (0 <= j) && (j < vCount()) ); // i,j 的合法性 162 163 if( ret ) 164 { 165 if( m_edges[i][j] != NULL ) // 权值存在,可以拿到 166 { 167 value = *(m_edges[i][j]); // 获取元素,这里面存储的是指针,所以要加 * 168 } 169 else 170 { 171 THROW_EXCEPTION(InvalidOperationException, "No value assigened to this edge ..."); 172 } 173 } 174 175 return ret; 176 } 177 178 /* 设置边上面权值的操作 */ 179 bool setEdge(int i, int j, const E& value) // O(1) 180 { 181 bool ret = ( (0 <= i) && (i < vCount()) && 182 (0 <= j) && (j < vCount()) ); // i,j 的合法性 183 184 if( ret ) 185 { 186 E* ne = m_edges[i][j]; // 使用中间变量 187 188 if( ne == NULL ) // i 到 j 本来不可达 189 { 190 ne = new E(); // 创建可达对象,设置 i 到 j 的连接 191 192 if( ne != NULL ) // 创建成功 193 { 194 *ne = value; // 设置权值 195 m_edges[i][j] = ne; // i 到 j 是可达的 196 m_eCount++; // 边数加 1 197 } 198 else 199 { 200 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to store new edge value ..."); 201 } 202 } 203 else 204 { 205 *ne = value; // 改变权值 206 } 207 } 208 209 return ret; 210 } 211 212 /* 删除 i 和 j 之间的关联,即没有边了 */ 213 bool removeEdge(int i, int j) // O(1) 214 { 215 bool ret = ( (0 <= i) && (i < vCount()) && 216 (0 <= j) && (j < vCount()) ); // i,j 的合法性 217 218 if( ret ) 219 { 220 E* toDel = m_edges[i][j]; // 定义中间变量指针指向要删除的权值对象 221 m_edges[i][j] = NULL; // 中间指针指向要删除的对象了,将邻接矩阵对应元素赋为空值 222 223 if( toDel != NULL ) 224 { 225 m_eCount--; // 边个数减一 226 delete toDel; // 为了尽量的达到异常安全目的,释放 m_edges 所指向的对象; 227 } 228 } 229 230 return ret; 231 } 232 233 /* 获取当前图中顶点的数量 */ 234 int vCount() // O(1) 235 { 236 return N; // 顶点的数量为当前模板参数 N,顶点数量是一个定制; 237 } 238 239 /* 获取当前图中边的数量 */ 240 int eCount() // O(1) 241 { 242 return m_eCount; // 添加边和删除边其都相应的变化 243 } 244 245 /* 顶点 i 的出度,i 行不为 0 的个数 */ 246 int OD(int i) // O(n) 247 { 248 int ret = 0; 249 if( (0 <= i) && (i < vCount()) ) 250 { 251 for(int j=0; j<vCount(); j++) // 数邻接矩阵对应的行中有多少个不为 0 的个数 252 { 253 if( m_edges[i][j] != NULL ) // 第 i 行不为 0 254 { 255 ret++; 256 } 257 } 258 } 259 else 260 { 261 THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ..."); 262 } 263 264 return ret; 265 } 266 267 /* 顶点 i 的入度,i 列不为 0 的个数 */ 268 int ID(int i) // O(n) 269 { 270 int ret = 0; 271 272 if( (0 <= i) && (i < vCount()) ) 273 { 274 for(int j=0; j<vCount(); j++) // 数邻接矩阵对应的列中有多少个不为 0 的个数 275 { 276 if( m_edges[j][i] != NULL ) // 第 i 列不为 0 277 { 278 ret++; 279 } 280 } 281 } 282 else 283 { 284 THROW_EXCEPTION(InvalidParameterException, "Index i is invalid ..."); 285 } 286 287 return ret; 288 } 289 290 291 ~MatrixGraph() // O(n*n) 292 { 293 for(int i=0; i<vCount(); i++) // 指针数组初始化 294 { 295 for(int j=0; j<vCount(); j++) 296 { 297 delete m_edges[i][j]; // 销毁每条边 298 } 299 300 delete m_vertexes[i] ; // 销毁和每个顶点相关联的数据元素 301 } 302 } 303 }; 304 305 } 306 307 #endif // MATRIXGRAPH_H
7,图的邻接矩阵结构实现测试代码:
1 #include <iostream> 2 #include "MatrixGraph.h" 3 4 using namespace std; 5 using namespace DTLib; 6 7 int main() 8 { 9 MatrixGraph<3, int, int> g; 10 11 g.setEdge(0, 1, 1); 12 g.setEdge(1, 0, 2); 13 g.setEdge(1, 2, 3); 14 15 cout << "vCount: " << g.vCount() << endl; 16 cout << "eCount: " << g.eCoutn() << endl; 17 18 cout << "ID(1): " << g.ID(1) << endl; 19 cout << "OD(1): " << g.OD(1) << endl; 20 cout << "TD(1): " << g.TD(1) << endl; 21 22 cout << "W(0, 1): " << g.getEdge(0, 1) << endl; 23 cout << "W(1, 0): " << g.getEdge(1, 0) << endl; 24 cout << "W(1, 2): " << g.getEdge(1, 2) << endl; 25 26 SharedPointer< Array<int> > aj = g.getAdgacent(2); 27 28 for(int i=0; i<aj->length(); i++) 29 { 30 cout << (*aj)[i] << " "; 31 } 32 33 cout << endl; 34 35 cout << "Delete Edge: " << endl; 36 37 g.removeEdge(0, 1); 38 39 cout << "eCount: " << g.eCoutn() << endl; 40 41 g.setVertex(0, 100); 42 43 cout << "V(0): " << g.getVertex(0) << endl; 44 45 //cout << "W(0, 1): " << g.getEdge(0, 1) << endl; // 非法操作 46 47 return 0; 48 }
8,小结:
1,邻接矩阵法使用数组对图相关的数据进行存储;
2,一维数组存储顶点相关的数据(空表示无相关的数据);
3,二维数组存储边相关的数据(空表示顶点间无连接);
4,代码实现时使用指针数组进行数据的存储(提高效率);