1,二叉树的克隆操作:
1,SharedPointer< BTree<T> > clone() const:
1,克隆当前树的一份拷贝;
2,返回值为堆空间中的一棵新二叉树(与当前树相等):
1,保存数据元素,树的属性一模一样;
2,二叉树的克隆的实现:

1,定义功能:clone(node)
1,拷贝 node 为根结点的二叉树(数据元素在对应位置相等);
2,功能函数代码实现:
1 /* 实现递归克隆函数,这个函数实现了结点之间的链接 */ 2 BTreeNode<T>* clone(BTreeNode<T>* node) const 3 { 4 BTreeNode<T>* ret = NULL; 5 6 if( node != NULL ) // 被克隆的二叉树非空 7 { 8 ret = BTreeNode<T>::NewNode(); 9 10 if( ret != NULL ) 11 { 12 ret->value = node->value; // 先将数据拷贝出来 13 ret->left = clone(node->left); 14 ret->right = clone(node->right); 15 16 if( ret->left != NULL ) // 左子树不为空,指定父子关系 17 { 18 ret->left->parent = ret; // 左子树父亲是当前结点 19 } 20 21 if( ret->right != NULL ) // 右子树不为空,指定父子关系 22 { 23 ret->right->parent = ret; // 右子树父亲是当前结点 24 } 25 } 26 else 27 { 28 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new node ..."); 29 } 30 } 31 32 return ret; 33 }
3,克隆成员函数代码实现:
1 /* 克隆一个二叉树 */ 2 SharedPointer< BTree<T> > clone() const 3 { 4 BTree<T>* ret = new BTree<T>(); 5 6 if( ret != NULL ) 7 { 8 ret->m_root = clone(root()); // 克隆当前树的根结点 9 } 10 else 11 { 12 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ..."); 13 } 14 15 return ret; 16 }
3,二叉树比较操作的定义:
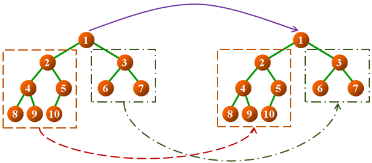
1,判断两棵二叉树中的数据元素是否对应相等(递归的实现):
1,bool operator == (const BTree<T>& btree)
2,bool operator != (const BTree<T>& btree)
1,二叉树的比较是递归进行的,因此要定义具体的相等功能;
4,二叉树的比较的实现:

1,定义功能:equal(lh, rh)
1,判断 lh 为根结点的二叉树与 rh 为根结点的二叉树是否相等;
2,功能函数代码实现:
1 /*实现两颗二叉树是否相等的递归功能函数,参数为两个根结点*/ 2 bool equal(BTreeNode<T>* lh, BTreeNode<T>* rh) const 3 { 4 if( lh == rh ) // 自己和自己比较,相等 5 { 6 return true; 7 } 8 else if( (lh != NULL) && (rh != NULL) ) 9 { /* 判断值、递归判断左子树和右子树是否相等 */ 10 return (lh->value == rh->value) && equal(lh->left, rh->left) && equal(lh->right, rh->right); 11 } 12 else 13 { 14 return false; // 一个二叉树为空树,另一颗二叉树不为空 15 } 16 }
3,相等和不等操作符重载的代码实现:
1 /* 两个二叉树相等 */ 2 bool operator == (const BTree<T>& btree) 3 { 4 return equal(root(), btree.root()); 5 } 6 7 /* 两颗二叉树不相等 */ 8 bool operator != (const BTree<T>& btree) 9 { 10 return !(*this == btree); 11 }
5,二叉树的相加操作:
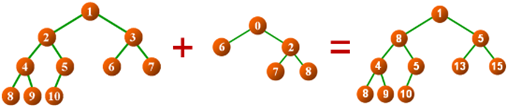
1,SharedPointer< BTree<T> > add(const BTree<T>& btree) const
1,将当前二叉树与参数 btree 中的数据元素在对应位置处相加;
2,返回值(相加的结果)为堆空间中的一棵新二叉树;
6,二叉树加法的实现:

1,定义功能:add(lh, rh)
1,将 lh 为根结点的二叉树与 rh 为根结点的二叉树相加;
2,前两中情况刚好对应了小树和大树相加中,小树部分为空、大树部分不为空的情形;
2,功能函数代码实现:
1 /* 两颗二叉树相加的功能函数 */ 2 BTreeNode<T>* add(BTreeNode<T>* lh, BTreeNode<T>* rh) const 3 { 4 BTreeNode<T>* ret = NULL; 5 6 if( (lh == NULL) && (rh != NULL) ) 7 { 8 ret = clone(rh); // 相加直接为非空的树 9 } 10 else if( (lh != NULL) && (rh == NULL) ) 11 { 12 ret = clone(lh); // 相加直接为非空的树 13 } 14 else if( (lh != NULL) && (rh != NULL) ) 15 { 16 ret = BTreeNode<T>::NewNode(); 17 18 if( ret != NULL ) 19 { 20 ret->value = lh->value + rh->value; // 结点的值直接相加 21 ret->left = add(lh->left, rh->left); // 递归实现左子树相加 22 ret->right = add(lh->right, rh->right); // 递归实现右子树相加 23 24 if( ret->left != NULL ) // 左子树父结点设置为当前的结点 25 { 26 ret->left->parent = ret; 27 } 28 29 if( ret->right != NULL ) // 右子树父结点设置为当前的结点 30 { 31 ret->right->parent = ret; 32 } 33 } 34 else 35 { 36 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new node ..."); 37 } 38 } 39 40 return ret; 41 }
3,相加成员函数代码实现:
1 /* 执行加法操作 */ 2 SharedPointer< BTree<T> > add(const BTree<T>& btree) const 3 { 4 BTree<T>* ret = new BTree<T>(); // 创建一棵要返回的树; 5 if( ret != NULL ) 6 { 7 ret->m_root = add(root(),btree.root()); // 以结点链接这个树; 8 } 9 else 10 { 11 THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ..."); 12 } 13 return ret; 14 }
7,小结:
1,比较操作判断两棵二叉树中的数据元素是否对应相等;
2,克隆操作将当前二叉树在堆空间中进行复制;
3,相加操作将两棵二叉树中的数据元素在对应位置处相加;
4,相加操作的结果保存在堆空间的一棵二叉树中;