1,已经创建了通用树结构,有必要创建另一种树结构吗?
2,简化树就直接减少结点中孩子的数量,但是这样树还能通用吗?
3,通用树结构的回顾:
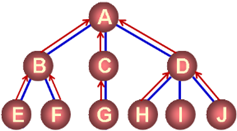
1,双亲孩子表示法:
1,每个结点都有一个指向双亲的指针;
2,每个结点都有若干个指向其孩子的指针;
4,另一种树结构模型:
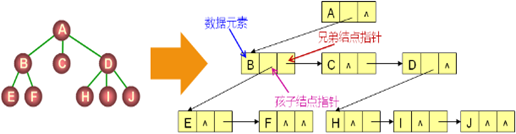
1,孩子兄弟表示法:
1,每个结点都有一个指向其第一个孩子的指针;
2,每个结点都有一个指向其第一个右兄弟的指针;
1,孩子兄弟表示法可以描述普通的树型结构,因为通过根结点可以访问到这一个树形结构的每一个结点;
5,孩子兄弟表示法的特点:
1,能够表示任意的树形结构;
2,每个结点包含一个数据成员和两个指针成员;
1,形态相对固定,实现相对简单;
3,孩子结点指针和兄弟结点指针构成了“树杈”;
1,二叉表示法就是“孩子兄弟”表示模型,其抽象后就是二叉树,但实现不是用“孩子兄弟”指针实现的;
2,二叉树是即将讨论的内容,不在关注通用树及其在二叉或者“孩子兄弟”表示法下是如何转换的,重点放在二叉树的相关内容创建和算法研究;
6,二叉树的定义:
1,二叉树是由 n(n >= 0)个结点组成的有限集合,该集合或者为空,或者是由一个根结点加上两颗分别称为左子树和右子树的、互不相交的二叉树组成;
7,二叉树五种形态:

1,二叉树结点只有三种形态,依据子结点数目分;
8,特殊二叉树:

1,满二叉树(Full Binary Tree):
1,如果二叉树中所有分支结点的度数都为 2,且叶子结点都在同一层次上,则称这类二叉树为满二叉树;
1,除了叶结点,任何分支结点度数都为 2,且叶结点在同一层次;
2,完全二叉树(Complete Binary Tree):
1,如果一棵具有 n 个结点的高度为 k 的二叉树,它的每一个结点都与高度为 k 的满二叉树编号为 1到 n 的结点一一对应,则称这棵树为完全二叉树。(从上到下从左到右编号)
9,完全二叉树特性:
1,同样结点数的二叉树,完全二叉树的高度最小;
1,按顺序排列的;
2,完全二叉树的叶结点仅出现在最下面两层:
1,最底层的叶结点一定出现在左边;
2,倒数第二层的叶结点一定出现在右边;
3,完全二叉树中度为 1 的结点只有左孩子;
1,完全二叉树是还没形成的满二叉树,满二叉树是完全二叉树;
10,小结:
1,通用树结构采用了双亲结点表示法进行描述;
2,孩子兄弟表示法有能力描述任意类型的树结构;
3,孩子兄弟表示法能够将通用树转化为二叉树;
4,二叉树是最多只有两个孩子的树;