/*题目描述
/* struct TreeNode { int val; struct TreeNode *left; struct TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) { } };*/ class Solution { public: void findPath( TreeNode* root, int expectNumber, vector<vector<int> > &resultPaths, vector<TreeNode*> &PathNode, vector<int> &everyPath, int currSum ) { TreeNode* p = root; currSum += p->val; PathNode.push_back(p); everyPath.push_back(p->val); if (currSum == expectNumber && (p->left == nullptr && p->right == nullptr)) { resultPaths.push_back(everyPath); } if (p->left != nullptr) findPath(p->left, expectNumber, resultPaths, PathNode, everyPath, currSum); if (p->right != nullptr) findPath(p->right, expectNumber, resultPaths, PathNode, everyPath, currSum); currSum -= everyPath[everyPath.size() - 1];//这句为什么可以不用也正确 everyPath.pop_back();/*因为是传引用的形式,每个递归函数的过程中都使用的是同一个vector,所以这里要pop,而currSum是传值,
每个函数中都不一样,都有一个对应的值,所以不需要写上面的那句*/ PathNode.pop_back(); } vector<vector<int> > FindPath(TreeNode* root, int expectNumber) { vector<vector<int>> resultPaths; vector<int> everyPath; vector<TreeNode*> PathNode; int currSum = 0;//传参数前int类型一定要初始化,后面计算要用到 if (root == nullptr) return resultPaths; findPath(root, expectNumber, resultPaths, PathNode, everyPath, currSum); return resultPaths; } };
//如果改为不传引用的方式,则可以不用最后几句pop的操作:
void findPath(
TreeNode* root,
int expectNumber,
vector<vector<int> > &resultPaths,
vector<TreeNode*> PathNode,
vector<int> everyPath,
int currSum
) {
TreeNode* p = root;
currSum += p->val;
PathNode.push_back(p);
everyPath.push_back(p->val);
if (currSum == expectNumber && (p->left == nullptr && p->right == nullptr)) {
resultPaths.push_back(everyPath);
}
if (p->left != nullptr)
findPath(p->left, expectNumber, resultPaths, PathNode, everyPath, currSum);
if (p->right != nullptr)
findPath(p->right, expectNumber, resultPaths, PathNode, everyPath, currSum);
currSum -= everyPath[everyPath.size() - 1];//这句为什么可以不用也正确
//everyPath.pop_back();/*因为是传引用的形式,每个递归函数的过程中都使用的是同一个vector,所以这里要pop,而currSum是传值,
每个函数中都不一样,都有一个对应的值,所以不需要写上面的那句*/
//PathNode.pop_back();
}
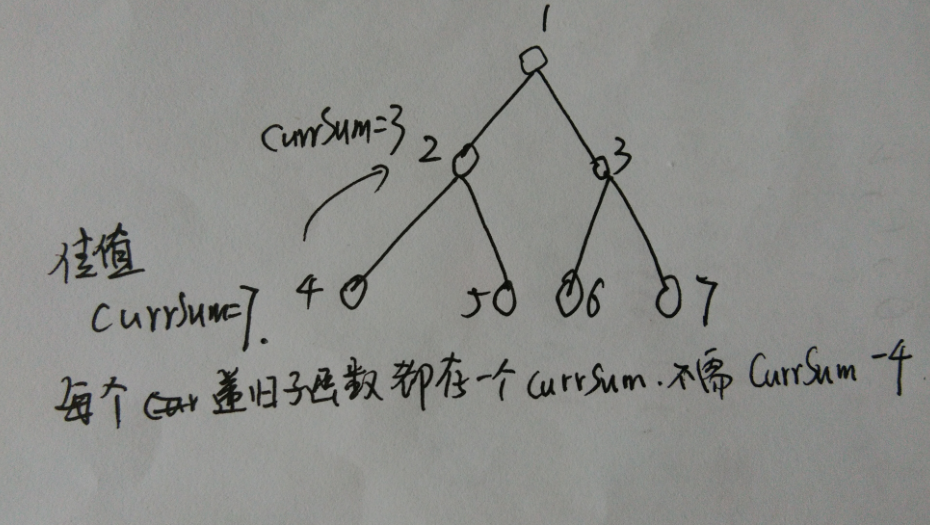
1)递归到2的那一层currSum保存一个3,4的那一层保存一个currSum=7,这两个只是名字不一样,是在不同的子函数中的,所以不需要写currSum-4.
如果改成传引用的方式,则在每一个函数中都是操作同一个currSum。就需要减去值。这里是传值得形式,每次都拷贝一个新的值,所以不需要相减。
函数递归的过程中需要将应该执行而未执行的程序代码依次保存下来,当递归结束程序回溯时将保留下来的程序代码用相反的次序一次执行一遍即可。
记得每次递归都会返回到上次执行的地方,上面的程序首先一直执行到最左边的叶子节点,然后弹出该节点,返回到上次调用的地方,接下来执行p->right。
不要把递归想的很神秘,其实就是函数的嵌套执执行。
******************************************************************************************************
2)以下转自其他博客对递归的解释。
http://chenqx.github.io/2014/09/29/Algorithm-Recursive-Programming/
计算机科学的新学生通常难以理解递归程序设计的概念。递归思想之所以困难,原因在于它非常像是循环推理(circular reasoning)。它也不是一个直观的过程;当我们指挥别人做事的时候,我们极少会递归地指挥他们。
Introduction
递归算法是一种直接或者间接调用自身函数或者方法的算法。递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效,它可以使算法简洁和易于理解。递归算法,其实说白了,就是程序的自身调用。它表现在一段程序中往往会遇到调用自身的那样一种coding策略,这样我们就可以利用大道至简的思想,把一个大的复杂的问题层层转换为一个小的和原问题相似的问题来求解的这样一种策略。递归往往能给我们带来非常简洁非常直观的代码形势,从而使我们的编码大大简化,然而递归的思维确实很我们的常规思维相逆的,我们通常都是从上而下的思维问题, 而递归趋势从下往上的进行思维。这样我们就能看到我们会用很少的语句解决了非常大的问题,所以递归策略的最主要体现就是小的代码量解决了非常复杂的问题。
递归算法解决问题的特点:
- 递归就是方法里调用自身。
- 在使用递增归策略时,必须有一个明确的递归结束条件,称为递归出口。
- 递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。
- 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等,所以一般不提倡用递归算法设计程序。
递归算法要求。递归算法所体现的“重复”一般有三个要求:
(1) 是每次调用在规模上都有所缩小(通常是减半);
(2) 是相邻两次重复之间有紧密的联系,前一次要为后一次做准备(通常前一次的输出就作为后一次的输入);
(3) 是在问题的规模极小时必须用直接给出解答而不再进行递归调用,因而每次递归调用都是有条件的(以规模未达到直接解答的大小为条件),无条件递归调用将会成为死循环而不能正常结束。
从递归的经典示例开始
计算阶乘
计算阶乘是递归程序设计的一个经典示例。计算某个数的阶乘就是用那个数去乘包括 1 在内的所有比它小的数。例如,factorial(5) 等价于 5*4*3*2*1,而 factorial(3) 等价于 3*2*1。
阶乘的一个有趣特性是,某个数的阶乘等于起始数(starting number)乘以比它小一的数的阶乘。例如,factorial(5) 与 5 * factorial(4) 相同。您很可能会像这样编写阶乘函数:
|
1
2
3
|
int factorial(int n){
return n * factorial(n - 1);
}
|
(注:本文的程序示例用C语言编写)
不过,这个函数的问题是,它会永远运行下去,因为它没有终止的地方。函数会连续不断地调用 factorial。 当计算到零时,没有条件来停止它,所以它会继续调用零和负数的阶乘。因此,我们的函数需要一个条件,告诉它何时停止。
由于小于 1 的数的阶乘没有任何意义,所以我们在计算到数字 1 的时候停止,并返回 1 的阶乘(即 1)。因此,真正的递归函数类似于:
|
1
2
3
4
5
6
|
int factorial(int n){
if(n == 1)
return 1;
else
return n * factorial(n - 1);
}
|
可见,只要初始值大于零,这个函数就能够终止。停止的位置称为 基线条件(base case)。基线条件是递归程序的 最底层位置,在此位置时没有必要再进行操作,可以直接返回一个结果。所有递归程序都必须至少拥有一个基线条件,而且 必须确保它们最终会达到某个基线条件;否则,程序将永远运行下去,直到程序缺少内存或者栈空间。
斐波纳契数列
斐波纳契数列(Fibonacci Sequence),最开始用于描述兔子生长的数目时用上了这数列。从数学上,费波那契数列是以递归的方法来定义:
这样斐波纳契数列的递归程序就可以非常清晰的写出来了:
|
1
2
3
4
5
6
|
int Fibonacci(int n){
if (n <= 1)
return n;
else
return Fibonacci(n-1) + Fibonacci(n-2);
}
|
递归程序的基本步骤
每一个递归程序都遵循相同的基本步骤:
(1) 初始化算法。递归程序通常需要一个开始时使用的种子值(seed value)。要完成此任务,可以向函数传递参数,或者提供一个入口函数, 这个函数是非递归的,但可以为递归计算设置种子值。
(2) 检查要处理的当前值是否已经与基线条件相匹配。如果匹配,则进行处理并返回值。
(3) 使用更小的或更简单的子问题(或多个子问题)来重新定义答案。
(4) 对子问题运行算法。
(5) 将结果合并入答案的表达式。
(6) 返回结果。
使用归纳定义
有时候,编写递归程序时难以获得更简单的子问题。 不过,使用 归纳定义的(inductively-defined)数据集 可以令子问题的获得更为简单。归纳定义的数据集是根据自身定义的数据结构 —— 这叫做 归纳定义(inductive definition)。
例如,链表就是根据其本身定义出来的。链表所包含的节点结构体由两部分构成:它所持有的数据,以及指向另一个节点结构体(或者是 NULL,结束链表)的指针。 由于节点结构体内部包含有一个指向节点结构体的指针,所以称之为是归纳定义的。
使用归纳数据编写递归过程非常简单。注意,与我们的递归程序非常类似,链表的定义也包括一个基线条件 —— 在这里是 NULL 指针。 由于 NULL 指针会结束一个链表,所以我们也可以使用 NULL 指针条件作为基于链表的很多递归程序的基线条件。
下面看两个例子。
链表求和示例
让我们来看一些基于链表的递归函数示例。假定我们有一个数字列表,并且要将它们加起来。履行递归过程序列的每一个步骤,以确定它如何应用于我们的求和函数:
(1) 初始化算法。这个算法的种子值是要处理的第一个节点,将它作为参数传递给函数。
(2) 检查基线条件。程序需要检查确认当前节点是否为 NULL 列表。如果是,则返回零,因为一个空列表的所有成员的和为零。
(3) 使用更简单的子问题重新定义答案。我们可以将答案定义为当前节点的内容加上列表中其余部分的和。为了确定列表其余部分的和, 我们针对下一个节点来调用这个函数。
(4) 合并结果。递归调用之后,我们将当前节点的值加到递归调用的结果上。
这样我们就可以很简单的写出链表求和的递归程序,实例如下:
|
1
2
3
4
5
|
int sum_list(struct list_node *l){
if(l == NULL)
return 0;
return l.data + sum_list(l.next);
}
|
汉诺塔问题
汉诺塔(Hanoi Tower)问题也是一个经典的递归问题,该问题描述如下:
汉诺塔问题:古代有一个梵塔,塔内有三个座A、B、C,A座上有64个盘子,盘子大小不等,大的在下,小的在上(如图)。有一个和尚想把这64个盘子从A座移到B座,但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘子始终保持大盘在下,小盘在上。
- 如果只有 1 个盘子,则不需要利用B塔,直接将盘子从A移动到C。
- 如果有 2 个盘子,可以先将盘子1上的盘子2移动到B;将盘子1移动到C;将盘子2移动到C。这说明了:可以借助B将2个盘子从A移动到C,当然,也可以借助C将2个盘子从A移动到B。
- 如果有3个盘子,那么根据2个盘子的结论,可以借助c将盘子1上的两个盘子从A移动到B;将盘子1从A移动到C,A变成空座;借助A座,将B上的两个盘子移动到C。
以此类推,上述的思路可以一直扩展到 n 个盘子的情况,将将较小的 n-1个盘子看做一个整体,也就是我们要求的子问题,以借助B塔为例,可以借助空塔B将盘子A上面的 n-1 个盘子从A移动到B;将A最大的盘子移动到C,A变成空塔;借助空塔A,将B塔上的 n-2 个盘子移动到A,将C最大的盘子移动到C,B变成空塔…
根据以上的分析,不难写出程序:
|
1
2
3
4
5
6
7
8
9
10
|
void Hanoi (int n, char A, char B, char C){
if (n==1){ //end condition
move(A,B);//‘move’ can be defined to be a print function
}
else{
Hanoi(n-1,A,C,B);//move sub [n-1] pans from A to B
move(A,C);//move the bottom(max) pan to C
Hanoi(n-1,B,A,C);//move sub [n-1] pans from B to C
}
}
|
将循环转化为递归
在下表中了解循环的特性,看它们可以如何与递归函数的特性相对比。
| Properties | Loops | Recursive functions |
|---|---|---|
| 重复 | 为了获得结果,反复执行同一代码块;以完成代码块或者执行 continue 命令信号而实现重复执行。 | 为了获得结果,反复执行同一代码块;以反复调用自己为信号而实现重复执行。 |
| 终止条件 | 为了确保能够终止,循环必须要有一个或多个能够使其终止的条件,而且必须保证它能在某种情况下满足这些条件的其中之一。 | 为了确保能够终止,递归函数需要有一个基线条件,令函数停止递归。 |
| 状态 | 循环进行时更新当前状态。 | 当前状态作为参数传递。 |
可见,递归函数与循环有很多类似之处。实际上,可以认为循环和递归函数是能够相互转换的。 区别在于,使用递归函数极少被迫修改任何一个变量 —— 只需要将新值作为参数传递给下一次函数调用。 这就使得您可以获得避免使用可更新变量的所有益处,同时能够进行重复的、有状态的行为。
下面还是以阶乘为例子,循环写法为:
|
1
2
3
4
5
6
7
8
|
int factorial(int n){
int product = 0;
while(n>0){
product *= n;
n--;
}
return product;
}
|
递归写法在第二节中已经介绍过了,这里就不重复了,可以比较一下。
尾递归介绍
对于递归函数的使用,人们所关心的一个问题是栈空间的增长。确实,随着被调用次数的增加,某些种类的递归函数会线性地增加栈空间的使用 —— 不过,有一类函数,即尾部递归函数,不管递归有多深,栈的大小都保持不变。尾递归属于线性递归,更准确的说是线性递归的子集。
函数所做的最后一件事情是一个函数调用(递归的或者非递归的),这被称为 尾部调用(tail-call)。使用尾部调用的递归称为 尾部递归。当编译器检测到一个函数调用是尾递归的时候,它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点,因为递归调用是当前活跃期内最后一条待执行的语句,于是当这个调用返回时栈帧中并没有其他事情可做,因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个,这样所使用的栈空间就大大缩减了,这使得实际的运行效率会变得更高。
让我们来看一些尾部调用和非尾部调用函数示例,以了解尾部调用的含义到底是什么:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int test1(){
int a = 3;
test1(); /* recursive, but not a tail call. We continue */
/* processing in the function after it returns. */
a = a + 4;
return a;
}
int test2(){
int q = 4;
q = q + 5;
return q + test1(); /* test1() is not in tail position.
* There is still more work to be
* done after test1() returns (like
* adding q to the result*/
}
int test3(){
int b = 5;
b = b + 2;
return test1(); /* This is a tail-call. The return value
* of test1() is used as the return value
* for this function.*/
}
int test4(){
test3(); /* not in tail position */
test3(); /* not in tail position */
return test3(); /* in tail position */
}
|
可见,要使调用成为真正的尾部调用,在尾部调用函数返回之前,对其结果 不能执行任何其他操作。
注意,由于在函数中不再做任何事情,那个函数的实际的栈结构也就不需要了。惟一的问题是,很多程序设计语言和编译器不知道 如何除去没有用的栈结构。如果我们能找到一个除去这些不需要的栈结构的方法,那么我们的尾部递归函数就可以在固定大小的栈中运行。
在尾部调用之后除去栈结构的方法称为 尾部调用优化 。
那么这种优化是什么?我们可以通过询问其他问题来回答那个问题:
(1) 函数在尾部被调用之后,还需要使用哪个本地变量?哪个也不需要。
(2) 会对返回的值进行什么处理?什么处理也没有。
(3) 传递到函数的哪个参数将会被使用?哪个都没有。
好像一旦控制权传递给了尾部调用的函数,栈中就再也没有有用的内容了。虽然还占据着空间,但函数的栈结构此时实际上已经没有用了,因此,尾部调用优化就是要在尾部进行函数调用时使用下一个栈结构 覆盖 当前的栈结构,同时保持原来的返回地址。
我们所做的本质上是对栈进行处理。再也不需要活动记录(activation record),所以我们将删掉它,并将尾部调用的函数重定向返回到调用我们的函数。 这意味着我们必须手工重新编写栈来仿造一个返回地址,以使得尾部调用的函数能直接返回到调用它的函数。
Conclusion
递归是一门伟大的艺术,使得程序的正确性更容易确认,而不需要牺牲性能,但这需要程序员以一种新的眼光来研究程序设计。对新程序员 来说,命令式程序设计通常是一个更为自然和直观的起点,这就是为什么大部分程序设计说明都集中关注命令式语言和方法的原因。 不过,随着程序越来越复杂,递归程序设计能够让程序员以可维护且逻辑一致的方式更好地组织代码。
References