ZOJ 4070

题目链接：http://acm.zju.edu.cn/onlinejudge/showContestProblem.do?problemId=5840

Time Limit: 1 Second　　Memory Limit: 65536 KB

If we define $f(0)=1,f(1)=0,f(4)=1,f(8)=2,f(16)=1 cdots$, do you know what function $f$ means?

Actually, $f(x)$ calculates the total number of enclosed areas produced by each digit in $x$. The following table shows the number of enclosed areas produced by each digit:

Enclosed Area	Digit	Enclosed Area	Digit
0	1	5	0
1	0	6	1
2	0	7	0
3	0	8	2
4	1	9	1

For example, $f(1234)=0+0+0+1=1$, and $f(5678)=0+1+0+2=3$.

We now define a recursive function  by the following equations:

 

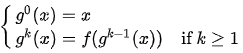
For example, $g^2(1234)=f(f(1234))=f(1)=0$, and $g^2(5678)=f(f(5678))=f(3)=0$.

Given two integers $x$ and $k$, please calculate the value of $g^k(x)$.

题解：

（浙大出题就是良心，又稳又好。）

 求 $k$ 层嵌套的 $f(x)$，因为几层 $f(x)$ 下去 $x$ 很快就变成 $0$ 或者 $1$ 了，这个时候，可以根据 $x$ 外面还剩下多少层 $f$ 直接返回 $0$ 或者 $1$。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int fx[10]={1,0,0,0,1,0,1,0,2,1};
int x,k;
int f(int x)
{
    int res=0;
    do{
        res+=fx[x%10];
        x/=10;
    }while(x);
    return res;
}
int g(int k,int x)
{
    while(k--)
    {
        x=f(x);
        if(x==0) return k%2;
        if(x==1) return 1-k%2;
    }
    return x;
}
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%d%d",&x,&k);
        printf("%d
",g(k,x));
    }
}