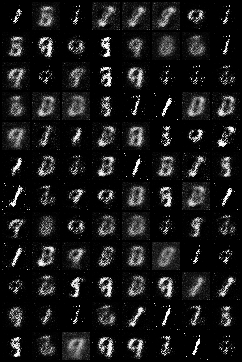目录
1 Divergence
1.1 Kullback–Leibler divergence
1.2 Jensen–Shannon divergence
1.3 Wasserstein distance
2 GAN
2.1 Theory
2.2 Algorithm
Objective function for generator in real implementation
Code
运行结果
1 Divergence
这是一些比较重要的前置知识。
1.1 Kullback–Leibler divergence
假设 $P(x), Q(x)$ 是随机变量 $X$ 的两个分布，在离散和连续随机变量的情形下，KL divergence 分别定义为：
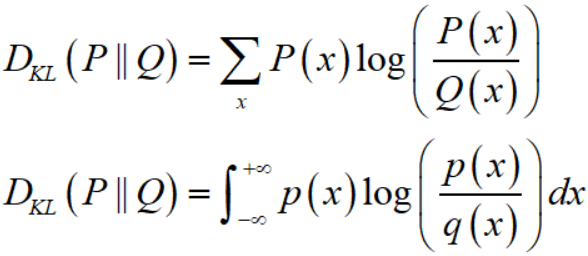
非负性：$D_{KL} (P parallel Q)$ 恒为非负的，且在 $P,Q$ 为同一分布时 $D_{KL} (P||Q) = 0$。
不对称性：$D_{KL} (P parallel Q) eq D_{KL} (Q||P)$。
1.2 Jensen–Shannon divergence
假设 $P(x), Q(x)$ 是随机变量 $X$ 的两个分布，Jensen–Shannon divergence 定义为：
其中 $M={frac {1}{2}}(P+Q)$。
JS divergence 解决了 KL divergence 不对称性的问题，一般地，JS divergence 是对称的，且取值 $0leq { m {JSD}}(Pparallel Q)leq log(2)$，注意这里的 $log$ 即 $ln$。
KL divergence 和 JS divergence 有一个同样的问题：如果两个分布 $P,Q$ 完全没有重叠，那么 KL divergence 是没有意义的，而 JS divergence 是一个常数 $log (2)$。
关于两个分布无重叠时 JS divergence 为 $log (2)$ 的证明也很简单：
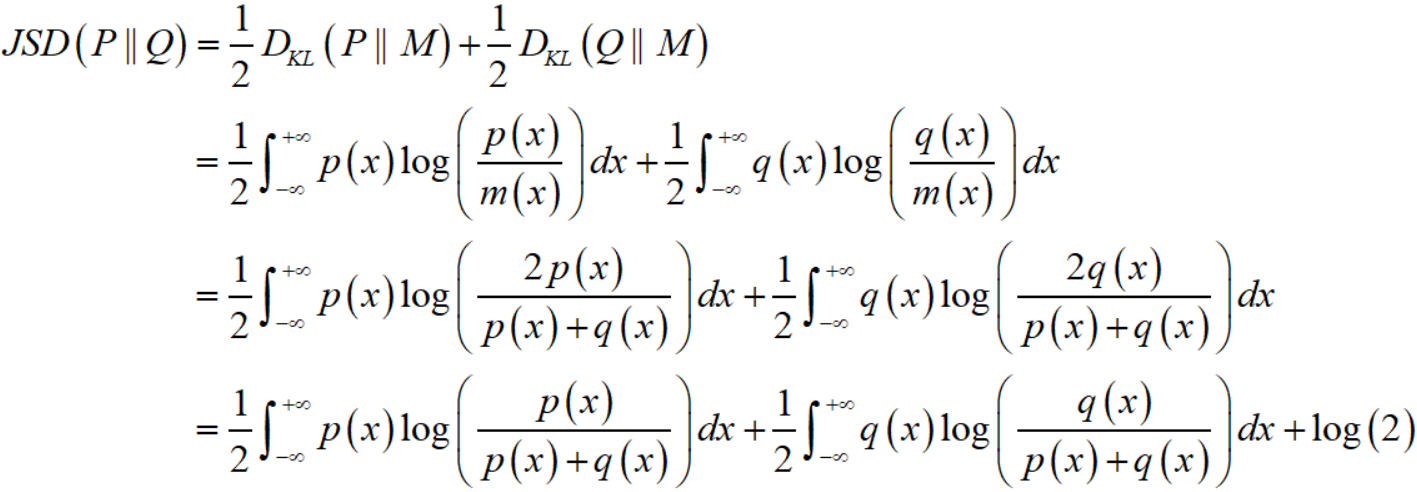
显然对于第一个积分，在 $p(x) eq 0$ 时必然有 $q(x) = 0$，所以第一个积分值为零。对第二个积分也是同理。所以两个分布无重叠时 JS divergence 为 $log (2)$。
1.3 Wasserstein distance
假设 $P, Q$ 是两个概率分布，则 Wasserstein distance 定义为：
其中，$gamma in Pi(x, y)$ 表示 $gamma$ 是一个联合分布，而它的边缘分布即 $P$ 和 $Q$。
如果 $P, Q$ 是连续型的概率分布，那么就有 $W(P,Q) = inf_{gamma in Pi[P,Q]} iint gamma(x,y)d(x,y)dxdy$。$d(x,y)$ 即 $left | x-y ight |$ 代表 $x,y$ 间的某种距离。
根据《从Wasserstein距离、对偶理论到WGAN》的说法，事实上 $gamma$ 描述了一种运输方案。假设 $P$ 是原始分布，$Q$ 是目标分布，$p(x)$ 的意思是原来在位置 $x$ 处有 $p(x)$ 数量的货物，而 $q(x)$ 是指最终 $x$ 处要存放的货物数量，如果某处 $x$ 的 $p(x)>q(x)$，那么就要把 $x$ 处的一部分货物运到别处，反之，如果 $p(x)<q(x)$，那么就要从别的地方运一些货物到 $x$ 处。而 $gamma(x,y)$ 的意思是指，要从 $x$ 处搬 $γ(x,y)$ 数量的东西到 $y$ 处。
最后是 $inf$，表示下确界，简单来说就是取最小，也就是说，要从所有的运输方案中，找出总运输成本 $iint gamma(x,y)d(x,y)dxdy$ 最小的方案，这个方案的成本，就是我们要算的 $W(P,Q)$。如果将上述比喻中的“货物”换成“沙土”，那么Wasserstein距离就是在求最省力的“搬土”方案了，所以Wasserstein距离也被称为“推土机距离”（Earth Mover's Distance）。更加形象的讲解可以参考李宏毅老师的GAN课程中关于WGAN的那一节。
2 GAN
2.1 Theory
We want to find data distribution $P_{data}(x)$，$x$ 是一张图片（或者说是a high-dimensional vector）， $P_{data}(x)$ 是一个固定的分布，而我们的database中的图片，都是来自 $P_{data}(x)$ 的一个个sample，如下图
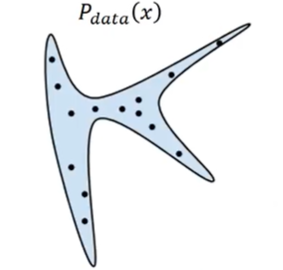
为了方便，图中的 $x$ 是二维空间中的一个点（一个向量）。
如果我们的database是二次元人物头像的，那么就有一个对应的固定的 $P_{data}(x)$，database里二次元人物头像图片，就是data points from distribution $P_{data}(x)$。很显然，往往这个分布中高概率的区域只占整个image space的很小很小的一部分。
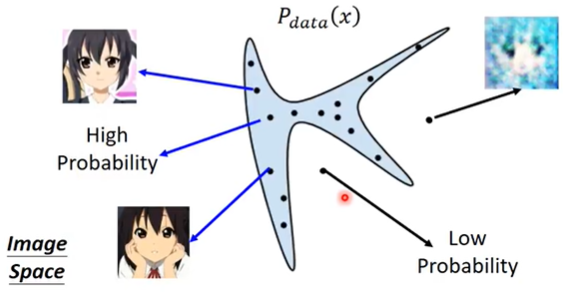
（假设蓝色区域就是高概率区域，而剩余的就是低概率区域）
显然， 我们不可能知道 $P_{data}(x)$ 的公式是怎么样的，我们唯一能做的事情就是sample from $P_{data}(x)$。
我们能做的事情就是：我们有一个distribution $P_G (x; heta)$ parameterized by $ heta$，通过调整参数 $ heta$ 使得 $P_G (x; heta)$ 接近 $P_{data}(x)$。
很自然，我们就能想到maximum likelihood estimation (MLE)：
假设我们有样本 ${x_1, cdots, x_m}$ 来自 $P_{data}(x)$，那么likelihood function
log-likelihood function为
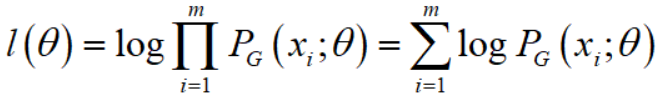
那么
也就是说，我们用MLE来估计 $ heta$，就约等于在minimize KL divergence。
（由于 $int_{x} log(P_{data}(x)) cdot P_{data}(x) dx$ 与 $ heta$ 无关，所以加上这一项并不影响 $argmaxlimits_{ heta}$）
（关于上面的约等于号怎么来的，参考伯努利大数定律，假设 $x$ 只有 $n$ 个可能的取值，表示成 $x^{(1)}, x^{(2)}, cdots, x^{(n)}$，当 $m$ 很大时，$m$ 个样本中取值为 $x^{(k)}$ 的样本，其数目占总样本数的比例 $frac{count(x^{(k)})}{m}$，就约等于 $P_{data}(x^{(k)})$，所以 $sum_{i=1}^{m} f(x_i) = sum_{k=1}^{n} frac{count(x^{(k)})}{m} f(x^{(k)}) approx sum_{k=1}^{n} P_{data}(x^{(k)}) f(x^{(k)}) = E_{x sim P_{data}}[f(x)]$。当然，这不是严格证明，这仅仅是我在思考这个约等于号时的一点思路。）
上面这个经典的MLE思路当然是可行的，如果我们可以先确定 $P_G(x; heta)$ 的表达式，那么就可以通过MLE求出 $hat{ heta}$，进而得到一个确定的 $P_G(x;hat{ heta})$，就可以sample from $P_G(x;hat{ heta})$ 来生成图片了，但实际上这样的效果并不好，因为 $P_{data}$ 其实是非常复杂的，我们需要更加复杂的 $P_G$ 来接近 $P_{data}$。
我们令 $G$ 是一个mapping，输入一个随机噪声 $z$，输出一个高维向量（图片） $x = G(z)$，随机噪声 $z$ 可能服从Gaussian distribution，也可能服从uniform distribution，关系不大，但是经过 $G$ 之后，$x$ 就可以服从一个非常复杂的distribution $P_{G}$。
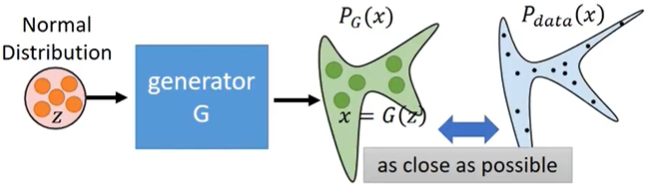
所以有
即寻找一个 $G^{*}$ 使得 $P_{data}$ 和 $P_G$ 之间的某种divergence最小。这个divergence可以是KL divergence，也可以是别的divergence。minimize KL divergence只不过是正好近似等价于MLE罢了。
然后问题就来了，由于 $P_{data}$ 是不可知的，而且如果mapping $G$ 很复杂的话，那么 $P_{G}$ 其实也是不可知的，所以我们其实没办法直接去算 $P_{data}$ 和 $P_G$ 之间的divergence，这就引出了discriminator的作用。
discriminator其实也是一个mapping，记作做 $D$，输入是一个高维向量（图像）$x$，输出是一个标量，$D$ 的作用是，分辨输入的图像到底是来自 $P_{data}$，还是来自 $P_G$。我们训练discriminator的做法如下：
Objective function for $D$：
注意，这里的 $G$ 是固定的，也就是说此时对于 $D$ 来说 $P_G$ 是固定的。
训练：
给定 $G$，最优的 $D^{*}$ 会最大化
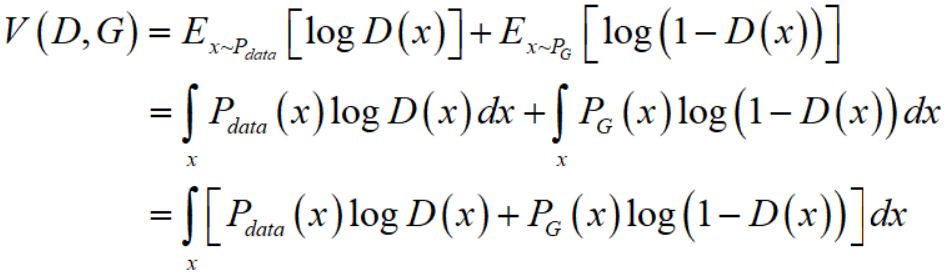
我们需要假设 $D(x)$ 是可以是任意函数，那么对于任意的 $x_1 eq x_2$，$D(x_1)$ 和 $D(x_2)$ 之间其实没有任何的相互限制，所以可以把每个 $x$ 分开来看待，
所以进一步给定 $x$，最优的 $D^{*}$ 会最大化
记 $a = P_{data}(x), b = P_G(x)$，记 $f(D) = a log(D) + b log(1-D)$，则令 $frac{df}{dD}$ 等于 $0$ 得到
如果我们绘制 $f(D) = 0.5 log(D) + 0.5 log(1-D)$ 的图像
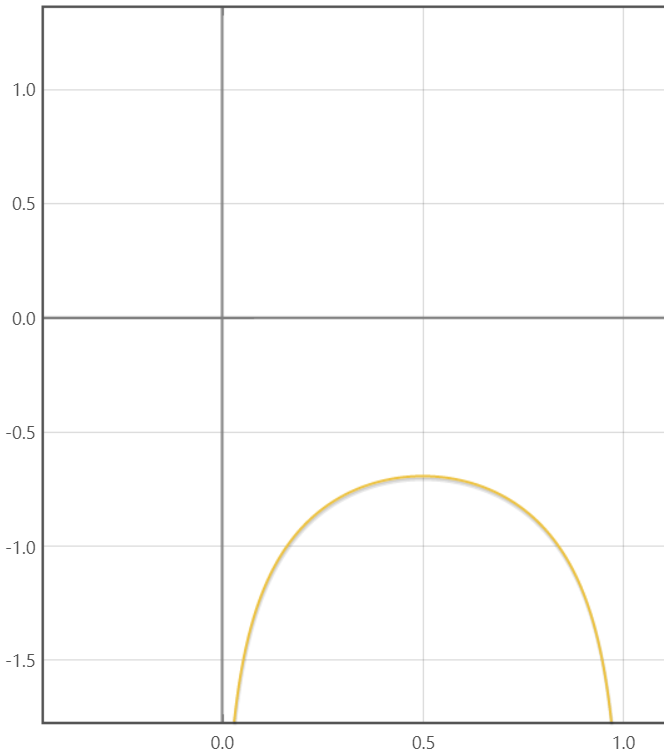其实无论 $a,b$ 在 $(0,1)$ 之间如何变动，该函数始终只有一个最大值，因此上面的方法是可行的。
因此，我们找到了 $D^{*}$，将其回代就可以得到
因此，我们现在有一种divergence $D(P_{data}, P_{G}) = 2JSD(P_{data} parallel P_{G}) - 2log2 = maxlimits_{D}V(D,G)$，所以将这个 $D(P_{data}, P_{G}) = maxlimits_{D}V(D,G)$ 代回到 $G^{*} = argminlimits_{G} D(P_{data}, P_{G})$ 中即可得
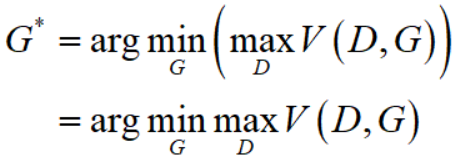
这就是《Generative Adversarial Nets》中式(1)
这里的 $p_{z}(z)$ 是随机噪声所服从的分布。
这里的 $minlimits_{G}maxlimits_{D}V(D,G)$ 似乎有些绕，其实并不难理解。从朴素的思想来看，我要寻找一个最优的 $G^{*}$ 使得divergence $D(P_{data}, P_{G})$ 最小，那就枚举所有可能的 $G$ 好了，看看哪个算出来的divergence $D(P_{data}, P_{G})$ 最小不就好了。那么对于一个给定的 $G = G'$，我们不会算 $D(P_{data}, P_{G})$，但是我知道 $D(P_{data}, P_{G}) = maxlimits_{D}V(D,G)$，注意此时的 $G'$ 是给定的，所以 $D(P_{data}, P_{G}) = maxlimits_{D}V(D,G') = maxlimits_{D}V(D)$，这就很简单了，我们也会算了，不就是找一个自变量为 $D$ 的一元函数 $V(D)$ 的最大值嘛，找到这个函数的最大值，这个值就是当 $G = G'$ 时的divergence $D(P_{data}, P_{G})$。然后我们就可以去枚举下一个 $G = G''$ 了。
2.2 Algorithm
上面我说的那种朴素的枚举所有可能的 $G$ 的思路显然是不可能真的去实现的，求最大值、最小值的一个经典方法就是梯度下降法。
首先记 $ heta_{G}$ 是 mapping $G$ 的参数，$ heta_{D}$ 是 mapping $D$ 的参数。
上述算法存在的一个问题是，例如，当我找到了 $D_{0}^{*}$ 使得 $V(D,G_0)$ 取得最大值，但是经过 $ heta_G leftarrow heta_G - eta cdot partial V(D_{0}^{*},G) / partial heta_G$ 更新之后，$G$ 已经变成了 $G_1$，$V(D,G_0)$ 和 $V(D,G_1)$ 这两个自变量为 $D$ 的函数，很可能差别比较大，例如下图
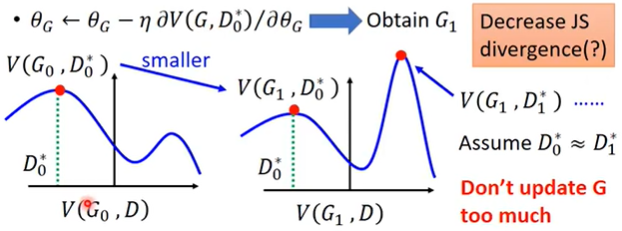
那么 $V(D,G_1)$ 的最大值很有可能反而比 $V(D,G_0)$ 的最大值还要大，换句话说，当我的 $G$ 从 $G_0$ 更新到 $G_1$，使得 $P_{data}$ 和 $P_G$ 之间的divergence反而增大了，这些然不是我们想要的情况。因此我们必须使得 $ heta_G$ 的更新尽量小一些，这样 $V(D,G_1)$ 和 $V(D,G_0)$ 这两个自变量为 $D$ 的函数的形状就会比较相似，就不会出现使得divergence反而增大的情况。
训练 $D$ 是在计算divergence，而训练 $G$ 是在降低divergence。
Objective function for generator in real implementation
对于generator的objective function $V = E_{x sim P_G}[log(1-D(x))]$，由于在一开始discriminator很容易区分图片的真假，所以它对于 $x sim P_G$ 给出的 $D(x)$ 值是很小的，这就导致 $log(1-D(x))$ 的导数值很小，使得训练速度偏慢。
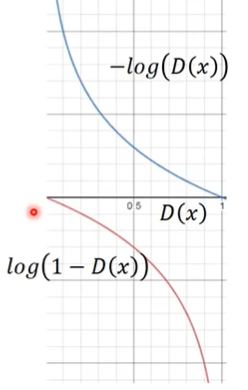
所以就把generator的objective function改成了 $V = E_{x sim P_G}[-log(D(x))]$。仅仅是因为两者的趋势是一致的，仅仅是因为斜率不一样，所以作者认为这样是可以的。
两者分别有命名
Code
import torch import torchvision import torch.nn as nn import torch.nn.functional as F from torchvision import datasets from torchvision import transforms from torchvision.utils import save_image from torch.autograd import Variable import os if not os.path.exists('./img'): os.mkdir('./img') def to_img(x): out = 0.5 * (x + 1) out = out.clamp(0, 1) out = out.view(-1, 1, 28, 28) return out batch_size = 128 num_epoch = 100 z_dimension = 100 # Image processing img_transform = transforms.Compose([ transforms.ToTensor(), transforms.Normalize(mean=[0.5], std=[0.5]) ]) # MNIST dataset mnist = datasets.MNIST( root='./data/', train=True, transform=img_transform, download=True) # Data loader dataloader = torch.utils.data.DataLoader( dataset=mnist, batch_size=batch_size, shuffle=True) class Discriminator(nn.Module): def __init__(self): super(Discriminator, self).__init__() self.dis = nn.Sequential( nn.Linear(784, 256), nn.LeakyReLU(0.2), nn.Linear(256, 256), nn.LeakyReLU(0.2), nn.Linear(256, 1), nn.Sigmoid()) def forward(self, x): return self.dis(x) class Generator(nn.Module): def __init__(self): super(Generator, self).__init__() self.gen = nn.Sequential( nn.Linear(100, 256), nn.ReLU(True), nn.Linear(256, 256), nn.ReLU(True), nn.Linear(256, 784), nn.Tanh()) def forward(self, x): return self.gen(x) D = Discriminator().cuda() G = Generator().cuda() # Binary cross entropy loss and optimizer criterion = nn.BCELoss() d_optimizer = torch.optim.Adam(D.parameters(), lr=0.0003) g_optimizer = torch.optim.Adam(G.parameters(), lr=0.0003) # Start training for epoch in range(num_epoch): for i, (img, _) in enumerate(dataloader): num_img = img.size(0) # region Train discriminator img = img.view(num_img, -1) real_img = img.cuda() real_label = torch.ones([num_img, 1]).cuda() fake_label = torch.zeros([num_img, 1]).cuda() # compute loss of real_img real_out = D(real_img) d_loss_real = criterion(real_out, real_label) real_scores = real_out # closer to 1 means better # compute loss of fake_img z = torch.randn(num_img, z_dimension).cuda() fake_img = G(z) fake_out = D(fake_img) d_loss_fake = criterion(fake_out, fake_label) fake_scores = fake_out # closer to 0 means better # bp and optimize d_loss = d_loss_real + d_loss_fake d_optimizer.zero_grad() d_loss.backward() d_optimizer.step() # endregion # region train generator # compute loss of fake_img z = torch.randn(num_img, z_dimension).cuda() fake_img = G(z) output = D(fake_img) g_loss = criterion(output, real_label) # bp and optimize g_optimizer.zero_grad() g_loss.backward() g_optimizer.step() # endregion if (i + 1) % 100 == 0: print('Epoch [{}/{}], d_loss: {:.6f}, g_loss: {:.6f}, ' 'D real: {:.6f}, D fake: {:.6f}.' .format(epoch, num_epoch, d_loss.item(), g_loss.item(), real_scores.data.mean(), fake_scores.data.mean())) if epoch == 0: real_images = to_img(real_img.cpu().data) save_image(real_images, './img/real_images.png') fake_images = to_img(fake_img.cpu().data) save_image(fake_images, './img/fake_images-{}.png'.format(epoch + 1))
关于BCELoss，即binary cross entropy loss，计算公式如下：
其中 $y_i$ 是真值的第 $i$ 项（注意取值是 $0$ 或者 $1$），而 $hat{y}_i$ 是对应的第 $i$ 项估计值（取值为 $[0,1]$）。而 $l_i$ 即对应的第 $i$ 项loss值。
而 nn.BCELoss() 中有一个参数 reduction='mean'，可以取值为 'mean' 或者 'sum' 或者 'none'，默认取值 'mean'，分别代表对上面的 $l_i$ 求均值、求和、不进一步操作。
所以上面的代码中，对于 $Dloss$ 有
所以梯度下降最小化 $Dloss$ 和之前的算法描述（Update discriminator parameters to maximize $widetilde{V} = frac{1}{m} sum_{i=1}^{m}log D(x^i) + frac{1}{m} sum_{i=1}^{m}log(1-D(widetilde{x}^i))$）是一致的。
而对于代码中的 $Gloss$ 有
梯度下降这也之前描述的在实际代码实现中用NSGAN而非MMGAN一致。
运行结果
这是运行了100 epochs中某几代的生成结果：
