1 关于人工智能、机器学习等各类名词的关系

可以看到,深度学习是机器学习的一个子集(不过这篇笔记主要记录一些传统的机器学习方法)。而且需要明确的是:深度学习和监督学习、非监督学习、强化学习这些概念,并不是按照同一个分类标准分出来的不同机器学习方法。
2 监督学习中的分类与回归
监督学习:利用一组带标签的数据,学习从输入到输出的映射,然后将这种映射关系应用到未知数据,达到分类或者回归的目的。
2.0 标称型数据和数值型数据
标称型数据:标称型目标变量的结果只在有限目标集中取值,如真与假(标称型目标变量主要用于分类)。
数值型数据:数值型目标变量则可以从无限的数值集合中取值,如0.100,42.001等(数值型目标变量主要用于回归)。
2.1 分类
分类:当输出是离散的,学习任务为分类任务;即分类主要用于预测标称型数据。
常见的分类方法有:k-近邻(kNN),朴素贝叶斯(Naive Bayes),支持向量机(SVM), 决策树(Decision Tree)。
有一个需要注意的方法是:Logistic回归,虽然名字里带“回归”,但它实际上是一种分类方法。
2.2 回归
回归:当输出是连续的,学习任务是回归任务;即回归主要用于预测数值型数据。
回归分析(Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照自变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多重线性回归分析。
多元和多重的区别:多重回归的英文是“multiple regerssion”,而多元回归是“multivariate regression”。两者是不同的概念,前者是一个因变量与多个自变量间的回归,后者是多个因变量与多个自变量间的回归。
3 线性回归
3.1 关于线性回归的形象描述
回归,最直接的办法是直接写出一个计算目标值的公式,假如你想要预测姐姐男友汽车的功率大小(Machine Learning in Action 这本书里这么举例子的),例如你自己琢磨出来可以这么计算:
$HorsePower = 0.0015 imes annualSalary - 0.99 imes hoursListeningToPublicRadio$
不管它是不是对的,总之我们有这么一个公式可以用来计算汽车的功率了。这就是一个回归方程(Regression Equation),而其中的 $0.0015$ 和 $-0.99$ 称作回归系数(Regression Weights)。当然,这两个回归系数是臆想出来的,我们可以去实际调查若干辆汽车,我们就会得到若干条关于 $HorsePower$、$annualSalary$ 和 $hoursListeningToPublicRadio$ 的数据,我们可以想出一些办法,用这些真实的数据,去求出更加可靠的回归系数,这样一个过程就是回归。
3.2 一元线性回归实例
这里我们依然使用 Machine Learning in Action 这本书里的实例(这里推荐一个《机器学习实战》源码和数据集的github项目:https://github.com/pbharrin/machinelearninginaction)。
《机器学习实战》书中给出了一个一元线性回归数据集“ex0.txt”:

1.000000 0.067732 3.176513 1.000000 0.427810 3.816464 1.000000 0.995731 4.550095 1.000000 0.738336 4.256571 1.000000 0.981083 4.560815 1.000000 0.526171 3.929515 1.000000 0.378887 3.526170 1.000000 0.033859 3.156393 1.000000 0.132791 3.110301 1.000000 0.138306 3.149813 1.000000 0.247809 3.476346 1.000000 0.648270 4.119688 1.000000 0.731209 4.282233 1.000000 0.236833 3.486582 1.000000 0.969788 4.655492 1.000000 0.607492 3.965162 1.000000 0.358622 3.514900 1.000000 0.147846 3.125947 1.000000 0.637820 4.094115 1.000000 0.230372 3.476039 1.000000 0.070237 3.210610 1.000000 0.067154 3.190612 1.000000 0.925577 4.631504 1.000000 0.717733 4.295890 1.000000 0.015371 3.085028 1.000000 0.335070 3.448080 1.000000 0.040486 3.167440 1.000000 0.212575 3.364266 1.000000 0.617218 3.993482 1.000000 0.541196 3.891471 1.000000 0.045353 3.143259 1.000000 0.126762 3.114204 1.000000 0.556486 3.851484 1.000000 0.901144 4.621899 1.000000 0.958476 4.580768 1.000000 0.274561 3.620992 1.000000 0.394396 3.580501 1.000000 0.872480 4.618706 1.000000 0.409932 3.676867 1.000000 0.908969 4.641845 1.000000 0.166819 3.175939 1.000000 0.665016 4.264980 1.000000 0.263727 3.558448 1.000000 0.231214 3.436632 1.000000 0.552928 3.831052 1.000000 0.047744 3.182853 1.000000 0.365746 3.498906 1.000000 0.495002 3.946833 1.000000 0.493466 3.900583 1.000000 0.792101 4.238522 1.000000 0.769660 4.233080 1.000000 0.251821 3.521557 1.000000 0.181951 3.203344 1.000000 0.808177 4.278105 1.000000 0.334116 3.555705 1.000000 0.338630 3.502661 1.000000 0.452584 3.859776 1.000000 0.694770 4.275956 1.000000 0.590902 3.916191 1.000000 0.307928 3.587961 1.000000 0.148364 3.183004 1.000000 0.702180 4.225236 1.000000 0.721544 4.231083 1.000000 0.666886 4.240544 1.000000 0.124931 3.222372 1.000000 0.618286 4.021445 1.000000 0.381086 3.567479 1.000000 0.385643 3.562580 1.000000 0.777175 4.262059 1.000000 0.116089 3.208813 1.000000 0.115487 3.169825 1.000000 0.663510 4.193949 1.000000 0.254884 3.491678 1.000000 0.993888 4.533306 1.000000 0.295434 3.550108 1.000000 0.952523 4.636427 1.000000 0.307047 3.557078 1.000000 0.277261 3.552874 1.000000 0.279101 3.494159 1.000000 0.175724 3.206828 1.000000 0.156383 3.195266 1.000000 0.733165 4.221292 1.000000 0.848142 4.413372 1.000000 0.771184 4.184347 1.000000 0.429492 3.742878 1.000000 0.162176 3.201878 1.000000 0.917064 4.648964 1.000000 0.315044 3.510117 1.000000 0.201473 3.274434 1.000000 0.297038 3.579622 1.000000 0.336647 3.489244 1.000000 0.666109 4.237386 1.000000 0.583888 3.913749 1.000000 0.085031 3.228990 1.000000 0.687006 4.286286 1.000000 0.949655 4.628614 1.000000 0.189912 3.239536 1.000000 0.844027 4.457997 1.000000 0.333288 3.513384 1.000000 0.427035 3.729674 1.000000 0.466369 3.834274 1.000000 0.550659 3.811155 1.000000 0.278213 3.598316 1.000000 0.918769 4.692514 1.000000 0.886555 4.604859 1.000000 0.569488 3.864912 1.000000 0.066379 3.184236 1.000000 0.335751 3.500796 1.000000 0.426863 3.743365 1.000000 0.395746 3.622905 1.000000 0.694221 4.310796 1.000000 0.272760 3.583357 1.000000 0.503495 3.901852 1.000000 0.067119 3.233521 1.000000 0.038326 3.105266 1.000000 0.599122 3.865544 1.000000 0.947054 4.628625 1.000000 0.671279 4.231213 1.000000 0.434811 3.791149 1.000000 0.509381 3.968271 1.000000 0.749442 4.253910 1.000000 0.058014 3.194710 1.000000 0.482978 3.996503 1.000000 0.466776 3.904358 1.000000 0.357767 3.503976 1.000000 0.949123 4.557545 1.000000 0.417320 3.699876 1.000000 0.920461 4.613614 1.000000 0.156433 3.140401 1.000000 0.656662 4.206717 1.000000 0.616418 3.969524 1.000000 0.853428 4.476096 1.000000 0.133295 3.136528 1.000000 0.693007 4.279071 1.000000 0.178449 3.200603 1.000000 0.199526 3.299012 1.000000 0.073224 3.209873 1.000000 0.286515 3.632942 1.000000 0.182026 3.248361 1.000000 0.621523 3.995783 1.000000 0.344584 3.563262 1.000000 0.398556 3.649712 1.000000 0.480369 3.951845 1.000000 0.153350 3.145031 1.000000 0.171846 3.181577 1.000000 0.867082 4.637087 1.000000 0.223855 3.404964 1.000000 0.528301 3.873188 1.000000 0.890192 4.633648 1.000000 0.106352 3.154768 1.000000 0.917886 4.623637 1.000000 0.014855 3.078132 1.000000 0.567682 3.913596 1.000000 0.068854 3.221817 1.000000 0.603535 3.938071 1.000000 0.532050 3.880822 1.000000 0.651362 4.176436 1.000000 0.901225 4.648161 1.000000 0.204337 3.332312 1.000000 0.696081 4.240614 1.000000 0.963924 4.532224 1.000000 0.981390 4.557105 1.000000 0.987911 4.610072 1.000000 0.990947 4.636569 1.000000 0.736021 4.229813 1.000000 0.253574 3.500860 1.000000 0.674722 4.245514 1.000000 0.939368 4.605182 1.000000 0.235419 3.454340 1.000000 0.110521 3.180775 1.000000 0.218023 3.380820 1.000000 0.869778 4.565020 1.000000 0.196830 3.279973 1.000000 0.958178 4.554241 1.000000 0.972673 4.633520 1.000000 0.745797 4.281037 1.000000 0.445674 3.844426 1.000000 0.470557 3.891601 1.000000 0.549236 3.849728 1.000000 0.335691 3.492215 1.000000 0.884739 4.592374 1.000000 0.918916 4.632025 1.000000 0.441815 3.756750 1.000000 0.116598 3.133555 1.000000 0.359274 3.567919 1.000000 0.814811 4.363382 1.000000 0.387125 3.560165 1.000000 0.982243 4.564305 1.000000 0.780880 4.215055 1.000000 0.652565 4.174999 1.000000 0.870030 4.586640 1.000000 0.604755 3.960008 1.000000 0.255212 3.529963 1.000000 0.730546 4.213412 1.000000 0.493829 3.908685 1.000000 0.257017 3.585821 1.000000 0.833735 4.374394 1.000000 0.070095 3.213817 1.000000 0.527070 3.952681 1.000000 0.116163 3.129283
由于一元线性回归的拟合直线可以用 $y = wx + b$ 表示,这里为了方便,将其表示成 $y = bx_0 + wx$,其中 $x_0$ 恒等于 $1$,因而数据集文件中第一列全为 $1$。
用Python绘制数据集对应的散点图如下图所示:
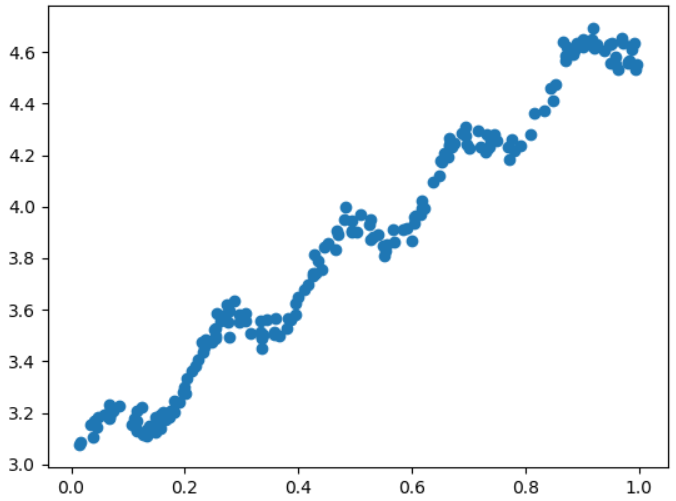
那么从理论上,如何从这么一大堆数据中求回归方程呢?假定某一条数据存放在向量 $mathbf{x}$ 中,实际值为 $y$,回归系数存放在向量 $mathbf{w}$ 中。
那么利用回归方程求得的预测值即为 $g_{mathbf{w}}(mathbf{x}) = mathbf{w}^T mathbf{x}$。
那么对于这条数据,必然会存在一个误差 $|g_{mathbf{w}}(mathbf{x}) - y|$,我们使用最小二乘法来的求解,最小二乘法的原则是以残差平方和最小来确定直线位置。
残差平方和可以写作:
$sum_{i=1}^{m}[g_{mathbf{w}}(mathbf{x}^{(i)}) - y^{(i)}]^2$
在这里,列向量 $mathbf{x}^{(i)}$ 以及 $y^{(i)}$ 分别代表第 $i$ 条数据的向量 $mathbf{x}$ 和实际值 $y$,$m$ 是样本数量。
给出关于损失函数、代价函数的定义:
损失函数(Loss Function)是定义在单个样本上的,算的是一个样本的误差。
代价函数(Cost Function)是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
根据代价函数的定义,我们可以给出代价函数:
$J(mathbf{w}) = frac{1}{2m} sum_{i=1}^{m}[g_{mathbf{w}}(mathbf{x}^{(i)}) - y^{(i)}]^2$
如果我们用设一个列向量 $E$ 为:
$mathbf{E} = [g_{mathbf{w}}(mathbf{x}^{(1)}) - y^{(1)}, g_{mathbf{w}}(mathbf{x}^{(2)}) - y^{(2)}, cdots, g_{mathbf{w}}(mathbf{x}^{(m)}) - y^{(m)}] ^ T$
根据这个 $E$ 的表示,如果我们设矩阵 $mathbf{X}$ 的第 $i$ 个行向量即为 $(mathbf{x}^{(i)}) ^ T$,列向量 $mathbf{y}$ 的第 $i$ 个元素是 $y^{(i)}$,那么我们可以进一步把 $E$ 表示为:
$mathbf{E} = mathbf{X}mathbf{w} - mathbf{y}$
那么 $2m$ 倍的代价函数可以表示为:
$2m cdot J(mathbf{w}) = mathbf{E}^T mathbf{E} = (mathbf{X}mathbf{w} - mathbf{y})^T (mathbf{X}mathbf{w} - mathbf{y})$
如果我们令代价函数对 $mathbf{w}$ 进行求导,并令其等于 $0$,即有:
$frac{d}{dmathbf{w}}(mathbf{X}mathbf{w} - mathbf{y})^T (mathbf{X}mathbf{w} - mathbf{y}) = mathbf{X}^T (mathbf{X}mathbf{w} - mathbf{y})= mathbf{0}$
得到:
$hat{mathbf{w}} = (mathbf{X}^T mathbf{X})^{-1} mathbf{X}^T mathbf{y}$
这个公式在Python中很好实现,另外需要注意判断方阵 $mathbf{X}^T mathbf{X}$ 是否为可逆,通过线性代数我们知道:可逆矩阵等价于非奇异矩阵,一个方阵是可逆的当且仅当其行列式不等于 $0$。
Python代码:

from numpy import * import matplotlib.pyplot as plt def loadDataSet(fileName): # 加载数据集文件 numFeat = len(open(fileName).readline().split(' ')) - 1 # open(fileName).readline() 从fileName指明的文件中读取第一行,返回一个字符串,即‘1.000000 0.067732 3.176513 ' # split(' ') 使用字符串类型的split()方法,按照' '将字符串分割,返回分割后的字符串组成的一个列表 # len()方法返回列表的长度 dataMat = []; labelMat = [] # 用分号分割在同一行上写的多条语句 fr = open(fileName) for line in fr.readlines(): # readlines()方法一次性读取整个文件,自动将文件变成每一行组成的列表 lineArr = [] curLine = line.strip().split(' ') # strip()方法用于移除字符串头尾指定的字符(默认为空格或换行符) for i in range(numFeat): # i = 0,1,...,numFeat-1 lineArr.append(float(curLine[i])) dataMat.append(lineArr) # dataMat相当于存储了前两列的数据的一个矩阵 labelMat.append(float(curLine[-1])) # curLine[-1] 即读取列表curLine的倒数第一个元素 return dataMat, labelMat def standRegres(xArr, yArr): # 计算最佳拟合直线 xMat = mat(xArr) # 转成矩阵类型 yMat = mat(yArr).T # 转成矩阵类型,由于是一个行向量,还需要进一步转置成列向量 xTx = xMat.T * xMat if linalg.det(xTx) == 0.0: # linalg.det()方法用来计算方阵的行列式 print('This matrix is singular, cannot do inverse.') return ws = xTx.I * (xMat.T * yMat) # xTx.I 矩阵xTx的逆矩阵 return ws xArr, yArr = loadDataSet('ex0.txt') ws = standRegres(xArr, yArr) print('Regression Weights is: ', ws[0], ' and ', ws[1]) # 输出回归系数 plt.scatter(asarray(xArr)[:, 1], asarray(yArr)) # 绘制散点图 plt.plot(asarray(xArr)[:, 1], asarray(xArr * ws)) # 绘制拟合函数 plt.show()
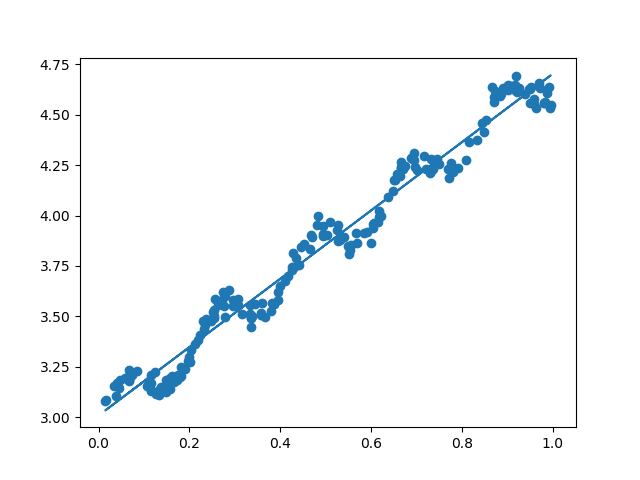
实验结果:
Regression Weights is: [[3.00774324]] and [[1.69532264]]
3.2 多元线性回归实例
对于同样的代价函数:
$J(mathbf{w}) = frac{1}{2m} sum_{i=1}^{m}[g_{mathbf{w}}(mathbf{x}^{(i)}) - y^{(i)}]^2$
这次我们使用另外一种叫做“梯度下降法”的方法来求回归系数。
3.2.1 梯度上升法
梯度上升法基于的思想是:要找到某个函数的最大值,最好的方法是沿着该函数的梯度方向探寻。
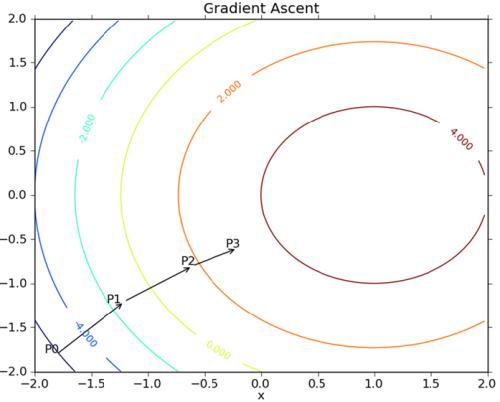
对于一个二元函数 $z = f(x,y)$,则对于其定义域上的某一个点 $(x,y)$ 可以定义一个向量 $(frac{partial f}{partial x},frac{partial f}{partial y})$,该向量就称为该函数在该点的梯度,记为 $ abla f(x,y)$。
梯度下降法和梯度上升法思想基本一致,只不过梯度下降法是用来求函数最小值的罢了。
因此,我们想要 $J(mathbf{w})$ 取得最小值,就可以使用梯度下降法($J(mathbf{w})$ 具有类似于“单峰”的性质)。
首先,为了求出梯度,我们要对 $mathbf{w}$ 中的每个元素分别进行偏导,得到:
$frac{partial}{partial w_j} J(mathbf{w}) = frac{1}{m} sum_{i=1}^{m}[g_{mathbf{w}}(mathbf{x}^{(i)}) - y^{(i)}]x_j^{(i)}$
此处 $w_j$ 代表列向量 $mathbf{w}$ 的第 $j$ 个元素,而 $x_j^{(i)}$ 则是列向量 $mathbf{x}^{(i)}$ 的第 $j$ 个元素,$j$ 是满足 $0 le j le n$ 的整数,因而列向量 $mathbf{x}^{(i)} = [x_0,x_1, cdots, x_n]$,其中$x_0$ 恒等于 $1$,作用与上面说到的相同,而 $m$ 依然是样本数量。
3.2.2 特征尺度变换
我们知道对于多维的特征向量 $mathbf{x}$,每一个维度往往具有不同的“尺度”。
如图所示,标准化前,由于变量的尺度相差很大,导致了椭圆型的梯度轮廓。标准化后,把变量变成统一单位,产生了近似于圆形的轮廓。由于梯度下降是按梯度方向下降,所以在椭圆轮廓上会迂回地寻找最优解,而圆形轮廓则可以较为直接地找到。而且,还存在一种比较极端的情况,有时没做标准化,模型始终找不到最优解,一直不收敛。

我们可以通过变量归一化来使得各个维度统一标准,归一化方法很多,例如:
线性归一化,也称min-max标准化、离差标准化;是对原始数据的线性变换,使得结果值映射到[0,1]之间:$frac{x_i - x_{min}}{x_{max} - x_{min}}$。
标准差归一化,也叫Z-score标准化,这种方法给予原始数据的均值 $μ$ 和标准差 $σ$ 进行数据的标准化。经过处理后的数据符合标准正态分布,即均值为 $0$,标准差为 $1$:$frac{x_i - mu}{sigma}$。
我们对于求函数 $J(mathbf{w})$ 的最小值,梯度下降法中最优的 $mathbf{w}$ 是迭代得到的:
$mathbf{w} := mathbf{w} - alpha cdot abla J(mathbf{w})$
其中 $alpha$ 是步长(学习率),很显然,这个值如果设定的太大,算法就无法收敛,如果设定的太小,算法收敛速度就偏慢。而要想确认当前设置的学习率 $alpha$ 是否使得算法收敛,只需要观察每次迭代后 $J(mathbf{w})$ 的值是否变小即可。
这里用的训练数据集是我们实验课上给的,应该就是网上那个波士顿房价数据集的精简:

0.538 6.575 4.09 15.3 24 0.469 6.421 4.9671 17.8 21.6 0.469 7.185 4.9671 17.8 34.7 0.458 6.998 6.0622 18.7 33.4 0.458 7.147 6.0622 18.7 36.2 0.458 6.43 6.0622 18.7 28.7 0.524 6.012 5.5605 15.2 22.9 0.524 6.172 5.9505 15.2 27.1 0.524 5.631 6.0821 15.2 16.5 0.524 6.004 6.5921 15.2 18.9 0.524 6.377 6.3467 15.2 15 0.524 6.009 6.2267 15.2 18.9 0.524 5.889 5.4509 15.2 21.7 0.538 5.949 4.7075 21 20.4 0.538 6.096 4.4619 21 18.2 0.538 5.834 4.4986 21 19.9 0.538 5.935 4.4986 21 23.1 0.538 5.99 4.2579 21 17.5 0.538 5.456 3.7965 21 20.2 0.538 5.727 3.7965 21 18.2 0.538 5.57 3.7979 21 13.6 0.538 5.965 4.0123 21 19.6 0.538 6.142 3.9769 21 15.2 0.538 5.813 4.0952 21 14.5 0.538 5.924 4.3996 21 15.6 0.538 5.599 4.4546 21 13.9 0.538 5.813 4.682 21 16.6 0.538 6.047 4.4534 21 14.8 0.538 6.495 4.4547 21 18.4 0.538 6.674 4.239 21 21 0.538 5.713 4.233 21 12.7 0.538 6.072 4.175 21 14.5 0.538 5.95 3.99 21 13.2 0.538 5.701 3.7872 21 13.1 0.538 6.096 3.7598 21 13.5 0.499 5.933 3.3603 19.2 18.9 0.499 5.841 3.3779 19.2 20 0.499 5.85 3.9342 19.2 21 0.499 5.966 3.8473 19.2 24.7 0.428 6.595 5.4011 18.3 30.8 0.428 7.024 5.4011 18.3 34.9 0.448 6.77 5.7209 17.9 26.6 0.448 6.169 5.7209 17.9 25.3 0.448 6.211 5.7209 17.9 24.7 0.448 6.069 5.7209 17.9 21.2 0.448 5.682 5.1004 17.9 19.3 0.448 5.786 5.1004 17.9 20 0.448 6.03 5.6894 17.9 16.6 0.448 5.399 5.87 17.9 14.4 0.448 5.602 6.0877 17.9 19.4 0.439 5.963 6.8147 16.8 19.7 0.439 6.115 6.8147 16.8 20.5 0.439 6.511 6.8147 16.8 25 0.439 5.998 6.8147 16.8 23.4 0.41 5.888 7.3197 21.1 18.9 0.403 7.249 8.6966 17.9 35.4 0.41 6.383 9.1876 17.3 24.7 0.411 6.816 8.3248 15.1 31.6 0.453 6.145 7.8148 19.7 23.3 0.453 5.927 6.932 19.7 19.6 0.453 5.741 7.2254 19.7 18.7 0.453 5.966 6.8185 19.7 16 0.453 6.456 7.2255 19.7 22.2 0.453 6.762 7.9809 19.7 25 0.4161 7.104 9.2229 18.6 33 0.398 6.29 6.6115 16.1 23.5 0.398 5.787 6.6115 16.1 19.4 0.409 5.878 6.498 18.9 22 0.409 5.594 6.498 18.9 17.4 0.409 5.885 6.498 18.9 20.9 0.413 6.417 5.2873 19.2 24.2 0.413 5.961 5.2873 19.2 21.7 0.413 6.065 5.2873 19.2 22.8 0.413 6.245 5.2873 19.2 23.4 0.437 6.273 4.2515 18.7 24.1 0.437 6.286 4.5026 18.7 21.4 0.437 6.279 4.0522 18.7 20 0.437 6.14 4.0905 18.7 20.8 0.437 6.232 5.0141 18.7 21.2 0.437 5.874 4.5026 18.7 20.3 0.426 6.727 5.4007 19 28 0.426 6.619 5.4007 19 23.9 0.426 6.302 5.4007 19 24.8 0.426 6.167 5.4007 19 22.9 0.449 6.389 4.7794 18.5 23.9 0.449 6.63 4.4377 18.5 26.6 0.449 6.015 4.4272 18.5 22.5 0.449 6.121 3.7476 18.5 22.2 0.489 7.007 3.4217 17.8 23.6 0.489 7.079 3.4145 17.8 28.7 0.489 6.417 3.0923 17.8 22.6 0.489 6.405 3.0921 17.8 22 0.464 6.442 3.6659 18.2 22.9 0.464 6.211 3.6659 18.2 25 0.464 6.249 3.615 18.2 20.6 0.445 6.625 3.4952 18 28.4 0.445 6.163 3.4952 18 21.4 0.445 8.069 3.4952 18 38.7 0.445 7.82 3.4952 18 43.8 0.445 7.416 3.4952 18 33.2 0.52 6.727 2.7778 20.9 27.5 0.52 6.781 2.8561 20.9 26.5 0.52 6.405 2.7147 20.9 18.6 0.52 6.137 2.7147 20.9 19.3 0.52 6.167 2.421 20.9 20.1 0.52 5.851 2.1069 20.9 19.5 0.52 5.836 2.211 20.9 19.5 0.52 6.127 2.1224 20.9 20.4 0.52 6.474 2.4329 20.9 19.8 0.52 6.229 2.5451 20.9 19.4 0.52 6.195 2.7778 20.9 21.7 0.547 6.715 2.6775 17.8 22.8 0.547 5.913 2.3534 17.8 18.8 0.547 6.092 2.548 17.8 18.7 0.547 6.254 2.2565 17.8 18.5 0.547 5.928 2.4631 17.8 18.3 0.547 6.176 2.7301 17.8 21.2 0.547 6.021 2.7474 17.8 19.2 0.547 5.872 2.4775 17.8 20.4 0.547 5.731 2.7592 17.8 19.3 0.581 5.87 2.2577 19.1 22 0.581 6.004 2.1974 19.1 20.3 0.581 5.961 2.0869 19.1 20.5 0.581 5.856 1.9444 19.1 17.3 0.581 5.879 2.0063 19.1 18.8 0.581 5.986 1.9929 19.1 21.4 0.581 5.613 1.7572 19.1 15.7 0.624 5.693 1.7883 21.2 16.2 0.624 6.431 1.8125 21.2 18 0.624 5.637 1.9799 21.2 14.3 0.624 6.458 2.1185 21.2 19.2 0.624 6.326 2.271 21.2 19.6 0.624 6.372 2.3274 21.2 23 0.624 5.822 2.4699 21.2 18.4 0.624 5.757 2.346 21.2 15.6 0.624 6.335 2.1107 21.2 18.1 0.624 5.942 1.9669 21.2 17.4 0.624 6.454 1.8498 21.2 17.1 0.624 5.857 1.6686 21.2 13.3 0.624 6.151 1.6687 21.2 17.8 0.624 6.174 1.6119 21.2 14 0.624 5.019 1.4394 21.2 14.4 0.871 5.403 1.3216 14.7 13.4 0.871 5.468 1.4118 14.7 15.6 0.871 4.903 1.3459 14.7 11.8 0.871 6.13 1.4191 14.7 13.8 0.871 5.628 1.5166 14.7 15.6 0.871 4.926 1.4608 14.7 14.6 0.871 5.186 1.5296 14.7 17.8 0.871 5.597 1.5257 14.7 15.4 0.871 6.122 1.618 14.7 21.5 0.871 5.404 1.5916 14.7 19.6 0.871 5.012 1.6102 14.7 15.3 0.871 5.709 1.6232 14.7 19.4 0.871 6.129 1.7494 14.7 17 0.871 6.152 1.7455 14.7 15.6 0.871 5.272 1.7364 14.7 13.1 0.605 6.943 1.8773 14.7 41.3 0.605 6.066 1.7573 14.7 24.3 0.871 6.51 1.7659 14.7 23.3 0.605 6.25 1.7984 14.7 27 0.605 7.489 1.9709 14.7 50 0.605 7.802 2.0407 14.7 50 0.605 8.375 2.162 14.7 50 0.605 5.854 2.422 14.7 22.7 0.605 6.101 2.2834 14.7 25 0.605 7.929 2.0459 14.7 50 0.605 5.877 2.4259 14.7 23.8 0.605 6.319 2.1 14.7 23.8 0.605 6.402 2.2625 14.7 22.3 0.605 5.875 2.4259 14.7 17.4 0.605 5.88 2.3887 14.7 19.1 0.51 5.572 2.5961 16.6 23.1 0.51 6.416 2.6463 16.6 23.6 0.51 5.859 2.7019 16.6 22.6 0.51 6.546 3.1323 16.6 29.4 0.51 6.02 3.5549 16.6 23.2 0.51 6.315 3.3175 16.6 24.6 0.51 6.86 2.9153 16.6 29.9 0.488 6.98 2.829 17.8 37.2 0.488 7.765 2.741 17.8 39.8 0.488 6.144 2.5979 17.8 36.2 0.488 7.155 2.7006 17.8 37.9 0.488 6.563 2.847 17.8 32.5 0.488 5.604 2.9879 17.8 26.4 0.488 6.153 3.2797 17.8 29.6 0.488 7.831 3.1992 17.8 50 0.437 6.782 3.7886 15.2 32 0.437 6.556 4.5667 15.2 29.8 0.437 7.185 4.5667 15.2 34.9 0.437 6.951 6.4798 15.2 37 0.437 6.739 6.4798 15.2 30.5 0.437 7.178 6.4798 15.2 36.4 0.401 6.8 6.2196 15.6 31.1 0.401 6.604 6.2196 15.6 29.1 0.422 7.875 5.6484 14.4 50 0.404 7.287 7.309 12.6 33.3 0.404 7.107 7.309 12.6 30.3 0.404 7.274 7.309 12.6 34.6 0.403 6.975 7.6534 17 34.9 0.403 7.135 7.6534 17 32.9 0.415 6.162 6.27 14.7 24.1 0.415 7.61 6.27 14.7 42.3 0.4161 7.853 5.118 14.7 48.5 0.4161 8.034 5.118 14.7 50 0.489 5.891 3.9454 18.6 22.6 0.489 6.326 4.3549 18.6 24.4 0.489 5.783 4.3549 18.6 22.5 0.489 6.064 4.2392 18.6 24.4 0.489 5.344 3.875 18.6 20 0.489 5.96 3.8771 18.6 21.7 0.489 5.404 3.665 18.6 19.3 0.489 5.807 3.6526 18.6 22.4 0.489 6.375 3.9454 18.6 28.1 0.489 5.412 3.5875 18.6 23.7 0.489 6.182 3.9454 18.6 25 0.55 5.888 3.1121 16.4 23.3 0.55 6.642 3.4211 16.4 28.7 0.55 5.951 2.8893 16.4 21.5 0.55 6.373 3.3633 16.4 23 0.507 6.951 2.8617 17.4 26.7 0.507 6.164 3.048 17.4 21.7 0.507 6.879 3.2721 17.4 27.5 0.507 6.618 3.2721 17.4 30.1 0.504 8.266 2.8944 17.4 44.8 0.504 8.725 2.8944 17.4 50 0.504 8.04 3.2157 17.4 37.6 0.504 7.163 3.2157 17.4 31.6 0.504 7.686 3.3751 17.4 46.7 0.504 6.552 3.3751 17.4 31.5 0.504 5.981 3.6715 17.4 24.3 0.504 7.412 3.6715 17.4 31.7 0.507 8.337 3.8384 17.4 41.7 0.507 8.247 3.6519 17.4 48.3 0.507 6.726 3.6519 17.4 29 0.507 6.086 3.6519 17.4 24 0.507 6.631 4.148 17.4 25.1 0.507 7.358 4.148 17.4 31.5 0.428 6.481 6.1899 16.6 23.7 0.428 6.606 6.1899 16.6 23.3 0.428 6.897 6.3361 16.6 22 0.428 6.095 6.3361 16.6 20.1 0.428 6.358 7.0355 16.6 22.2 0.428 6.393 7.0355 16.6 23.7 0.431 5.593 7.9549 19.1 17.6 0.431 5.605 7.9549 19.1 18.5 0.431 6.108 8.0555 19.1 24.3 0.431 6.226 8.0555 19.1 20.5 0.431 6.433 7.8265 19.1 24.5 0.431 6.718 7.8265 19.1 26.2 0.431 6.487 7.3967 19.1 24.4 0.431 6.438 7.3967 19.1 24.8 0.431 6.957 8.9067 19.1 29.6 0.431 8.259 8.9067 19.1 42.8 0.392 6.108 9.2203 16.4 21.9 0.392 5.876 9.2203 16.4 20.9 0.394 7.454 6.3361 15.9 44 0.647 8.704 1.801 13 50 0.647 7.333 1.8946 13 36 0.647 6.842 2.0107 13 30.1 0.647 7.203 2.1121 13 33.8 0.647 7.52 2.1398 13 43.1 0.647 8.398 2.2885 13 48.8 0.647 7.327 2.0788 13 31 0.647 7.206 1.9301 13 36.5 0.647 5.56 1.9865 13 22.8 0.647 7.014 2.1329 13 30.7 0.575 8.297 2.4216 13 50 0.575 7.47 2.872 13 43.5 0.464 5.92 3.9175 18.6 20.7 0.464 5.856 4.429 18.6 21.1 0.464 6.24 4.429 18.6 25.2 0.464 6.538 3.9175 18.6 24.4 0.464 7.691 4.3665 18.6 35.2 0.447 6.758 4.0776 17.6 32.4 0.447 6.854 4.2673 17.6 32 0.447 7.267 4.7872 17.6 33.2 0.447 6.826 4.8628 17.6 33.1 0.447 6.482 4.1403 17.6 29.1 0.4429 6.812 4.1007 14.9 35.1 0.4429 7.82 4.6947 14.9 45.4 0.4429 6.968 5.2447 14.9 35.4 0.4429 7.645 5.2119 14.9 46 0.401 7.923 5.885 13.6 50 0.4 7.088 7.3073 15.3 32.2 0.389 6.453 7.3073 15.3 22 0.385 6.23 9.0892 18.2 20.1 0.405 6.209 7.3172 16.6 23.2 0.405 6.315 7.3172 16.6 22.3 0.405 6.565 7.3172 16.6 24.8 0.411 6.861 5.1167 19.2 28.5 0.411 7.148 5.1167 19.2 37.3 0.411 6.63 5.1167 19.2 27.9 0.437 6.127 5.5027 16 23.9 0.437 6.009 5.5027 16 21.7 0.437 6.678 5.9604 16 28.6 0.437 6.549 5.9604 16 27.1 0.437 5.79 6.32 16 20.3 0.4 6.345 7.8278 14.8 22.5 0.4 7.041 7.8278 14.8 29 0.4 6.871 7.8278 14.8 24.8 0.433 6.59 5.4917 16.1 22 0.433 6.495 5.4917 16.1 26.4 0.433 6.982 5.4917 16.1 33.1 0.472 7.236 4.022 18.4 36.1 0.472 6.616 3.37 18.4 28.4 0.472 7.42 3.0992 18.4 33.4 0.472 6.849 3.1827 18.4 28.2 0.544 6.635 3.3175 18.4 22.8 0.544 5.972 3.1025 18.4 20.3 0.544 4.973 2.5194 18.4 16.1 0.544 6.122 2.6403 18.4 22.1 0.544 6.023 2.834 18.4 19.4 0.544 6.266 3.2628 18.4 21.6 0.544 6.567 3.6023 18.4 23.8 0.544 5.705 3.945 18.4 16.2 0.544 5.914 3.9986 18.4 17.8 0.544 5.782 4.0317 18.4 19.8 0.544 6.382 3.5325 18.4 23.1 0.544 6.113 4.0019 18.4 21 0.493 6.426 4.5404 19.6 23.8 0.493 6.376 4.5404 19.6 23.1 0.493 6.041 4.7211 19.6 20.4 0.493 5.708 4.7211 19.6 18.5 0.493 6.415 4.7211 19.6 25 0.493 6.431 5.4159 19.6 24.6 0.493 6.312 5.4159 19.6 23 0.493 6.083 5.4159 19.6 22.2 0.46 5.868 5.2146 16.9 19.3 0.46 6.333 5.2146 16.9 22.6 0.46 6.144 5.8736 16.9 19.8 0.4379 5.706 6.6407 16.9 17.1 0.4379 6.031 6.6407 16.9 19.4 0.515 6.316 6.4584 20.2 22.2 0.515 6.31 6.4584 20.2 20.7 0.515 6.037 5.9853 20.2 21.1 0.515 5.869 5.2311 20.2 19.5 0.515 5.895 5.615 20.2 18.5 0.515 6.059 4.8122 20.2 20.6 0.515 5.985 4.8122 20.2 19 0.515 5.968 4.8122 20.2 18.7 0.442 7.241 7.0379 15.5 32.7 0.518 6.54 6.2669 15.9 16.5 0.484 6.696 5.7321 17.6 23.9 0.484 6.874 6.4654 17.6 31.2 0.442 6.014 8.0136 18.8 17.5 0.442 5.898 8.0136 18.8 17.2 0.429 6.516 8.5353 17.9 23.1 0.435 6.635 8.344 17 24.5 0.429 6.939 8.7921 19.7 26.6 0.429 6.49 8.7921 19.7 22.9 0.411 6.579 10.7103 18.3 24.1 0.411 5.884 10.7103 18.3 18.6 0.41 6.728 12.1265 17 30.1 0.413 5.663 10.5857 22 18.2 0.413 5.936 10.5857 22 20.6 0.77 6.212 2.1222 20.2 17.8 0.77 6.395 2.5052 20.2 21.7 0.77 6.127 2.7227 20.2 22.7 0.77 6.112 2.5091 20.2 22.6 0.77 6.398 2.5182 20.2 25 0.77 6.251 2.2955 20.2 19.9 0.77 5.362 2.1036 20.2 20.8 0.77 5.803 1.9047 20.2 16.8 0.718 8.78 1.9047 20.2 21.9 0.718 3.561 1.6132 20.2 27.5 0.718 4.963 1.7523 20.2 21.9 0.631 3.863 1.5106 20.2 23.1 0.631 4.97 1.3325 20.2 50 0.631 6.683 1.3567 20.2 50 0.631 7.016 1.2024 20.2 50 0.631 6.216 1.1691 20.2 50 0.668 5.875 1.1296 20.2 50 0.668 4.906 1.1742 20.2 13.8 0.668 4.138 1.137 20.2 13.8 0.671 7.313 1.3163 20.2 15 0.671 6.649 1.3449 20.2 13.9 0.671 6.794 1.358 20.2 13.3 0.671 6.38 1.3861 20.2 13.1 0.671 6.223 1.3861 20.2 10.2 0.671 6.968 1.4165 20.2 10.4 0.671 6.545 1.5192 20.2 10.9 0.7 5.536 1.5804 20.2 11.3 0.7 5.52 1.5331 20.2 12.3 0.7 4.368 1.4395 20.2 8.8 0.7 5.277 1.4261 20.2 7.2 0.7 4.652 1.4672 20.2 10.5 0.7 5 1.5184 20.2 7.4 0.7 4.88 1.5895 20.2 10.2 0.7 5.39 1.7281 20.2 11.5 0.7 5.713 1.9265 20.2 15.1 0.7 6.051 2.1678 20.2 23.2 0.7 5.036 1.77 20.2 9.7 0.693 6.193 1.7912 20.2 13.8 0.693 5.887 1.7821 20.2 12.7 0.693 6.471 1.7257 20.2 13.1 0.693 6.405 1.6768 20.2 12.5 0.693 5.747 1.6334 20.2 8.5 0.693 5.453 1.4896 20.2 5 0.693 5.852 1.5004 20.2 6.3
测试数据集:

0.693 5.987 1.5888 20.2 5.6 0.693 6.343 1.5741 20.2 7.2 0.693 6.404 1.639 20.2 12.1 0.693 5.349 1.7028 20.2 8.3 0.693 5.531 1.6074 20.2 8.5 0.693 5.683 1.4254 20.2 5 0.659 4.138 1.1781 20.2 11.9 0.659 5.608 1.2852 20.2 27.9 0.597 5.617 1.4547 20.2 17.2 0.597 6.852 1.4655 20.2 27.5 0.597 5.757 1.413 20.2 15 0.597 6.657 1.5275 20.2 17.2 0.597 4.628 1.5539 20.2 17.9 0.597 5.155 1.5894 20.2 16.3 0.693 4.519 1.6582 20.2 7 0.679 6.434 1.8347 20.2 7.2 0.679 6.782 1.8195 20.2 7.5 0.679 5.304 1.6475 20.2 10.4 0.679 5.957 1.8026 20.2 8.8 0.718 6.824 1.794 20.2 8.4 0.718 6.411 1.8589 20.2 16.7 0.718 6.006 1.8746 20.2 14.2 0.614 5.648 1.9512 20.2 20.8 0.614 6.103 2.0218 20.2 13.4 0.584 5.565 2.0635 20.2 11.7 0.679 5.896 1.9096 20.2 8.3 0.584 5.837 1.9976 20.2 10.2 0.679 6.202 1.8629 20.2 10.9 0.679 6.193 1.9356 20.2 11 0.679 6.38 1.9682 20.2 9.5 0.584 6.348 2.0527 20.2 14.5 0.584 6.833 2.0882 20.2 14.1 0.584 6.425 2.2004 20.2 16.1 0.713 6.436 2.3158 20.2 14.3 0.713 6.208 2.2222 20.2 11.7 0.74 6.629 2.1247 20.2 13.4 0.74 6.461 2.0026 20.2 9.6 0.74 6.152 1.9142 20.2 8.7 0.74 5.935 1.8206 20.2 8.4 0.74 5.627 1.8172 20.2 12.8 0.74 5.818 1.8662 20.2 10.5 0.74 6.406 2.0651 20.2 17.1 0.74 6.219 2.0048 20.2 18.4 0.74 6.485 1.9784 20.2 15.4 0.74 5.854 1.8956 20.2 10.8 0.74 6.459 1.9879 20.2 11.8 0.74 6.341 2.072 20.2 14.9 0.74 6.251 2.198 20.2 12.6 0.713 6.185 2.2616 20.2 14.1 0.713 6.417 2.185 20.2 13 0.713 6.749 2.3236 20.2 13.4 0.713 6.655 2.3552 20.2 15.2 0.713 6.297 2.3682 20.2 16.1 0.713 7.393 2.4527 20.2 17.8 0.713 6.728 2.4961 20.2 14.9 0.713 6.525 2.4358 20.2 14.1 0.713 5.976 2.5806 20.2 12.7 0.713 5.936 2.7792 20.2 13.5 0.713 6.301 2.7831 20.2 14.9 0.713 6.081 2.7175 20.2 20 0.713 6.701 2.5975 20.2 16.4 0.713 6.376 2.5671 20.2 17.7 0.713 6.317 2.7344 20.2 19.5 0.713 6.513 2.8016 20.2 20.2 0.655 6.209 2.9634 20.2 21.4 0.655 5.759 3.0665 20.2 19.9 0.655 5.952 2.8715 20.2 19 0.584 6.003 2.5403 20.2 19.1 0.58 5.926 2.9084 20.2 19.1 0.58 5.713 2.8237 20.2 20.1 0.58 6.167 3.0334 20.2 19.9 0.532 6.229 3.0993 20.2 19.6 0.58 6.437 2.8965 20.2 23.2 0.614 6.98 2.5329 20.2 29.8 0.584 5.427 2.4298 20.2 13.8 0.584 6.162 2.206 20.2 13.3 0.614 6.484 2.3053 20.2 16.7 0.614 5.304 2.1007 20.2 12 0.614 6.185 2.1705 20.2 14.6 0.614 6.229 1.9512 20.2 21.4 0.532 6.242 3.4242 20.2 23 0.532 6.75 3.3317 20.2 23.7 0.532 7.061 3.4106 20.2 25 0.532 5.762 4.0983 20.2 21.8 0.583 5.871 3.724 20.2 20.6 0.583 6.312 3.9917 20.2 21.2 0.583 6.114 3.5459 20.2 19.1 0.583 5.905 3.1523 20.2 20.6 0.609 5.454 1.8209 20.1 15.2 0.609 5.414 1.7554 20.1 7 0.609 5.093 1.8226 20.1 8.1 0.609 5.983 1.8681 20.1 13.6 0.609 5.983 2.1099 20.1 20.1 0.585 5.707 2.3817 19.2 21.8 0.585 5.926 2.3817 19.2 24.5 0.585 5.67 2.7986 19.2 23.1 0.585 5.39 2.7986 19.2 19.7 0.585 5.794 2.8927 19.2 18.3 0.585 6.019 2.4091 19.2 21.2 0.585 5.569 2.3999 19.2 17.5
这里有一个我们需要注意的点,就是不像上面做的一元线性回归已经给出了一列全 $1$ 的 $x_0$,所以我们要自己添加这一列。
Python最小二乘法矩阵方法:

from numpy import * def loadDataSet(fileName): # 加载数据集文件 numFeat = len(open(fileName).readline().split(' ')) - 1 dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = [1.0] curLine = line.strip().split(' ') for i in range(numFeat): lineArr.append(float(curLine[i])) dataMat.append(lineArr) labelMat.append(float(curLine[-1])) return dataMat, labelMat def standRegres(xArr, yArr): xMat = mat(xArr) yMat = mat(yArr).T xTx = xMat.T * xMat if linalg.det(xTx) == 0.0: print('This matrix is singular, cannot do inverse.') return ws = xTx.I * (xMat.T * yMat) return ws def minmaxNorm(xMat): # 进行min-max标准化 for col in range(1, xMat.shape[1]): mini = min(asarray(xMat)[:, col]) maxi = max(asarray(xMat)[:, col]) for row in range(xMat.shape[0]): xMat[row, col] = (xMat[row, col] - mini) / (maxi - mini) return xMat xArr, yArr = loadDataSet('train_data.txt') xMat = minmaxNorm(mat(xArr)) yMat = mat(yArr) ws = standRegres(xMat, mat(yArr)) print('Regression Weights is: ', ws) # 输出回归系数
Python梯度下降法:

from numpy import * alpha = 0.5 maxStep = 1000 def loadDataSet(fileName): # 加载数据集文件 numFeat = len(open(fileName).readline().split(' ')) - 1 dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = [1.0] curLine = line.strip().split(' ') for i in range(numFeat): lineArr.append(float(curLine[i])) dataMat.append(lineArr) labelMat.append(float(curLine[-1])) return mat(dataMat), mat(labelMat).T def minmaxNorm(xMat): # 进行min-max标准化 for col in range(1, xMat.shape[1]): mini = min(asarray(xMat)[:, col]) maxi = max(asarray(xMat)[:, col]) for row in range(xMat.shape[0]): xMat[row, col] = (xMat[row, col] - mini) / (maxi - mini) return xMat def gradDes(xMat, yMat): # 梯度下降法 ws = mat(zeros((xMat.shape[1],1))) for step in range(maxStep): nab = mat(zeros((xMat.shape[1], 1))) for j in range(xMat.shape[1]): for i in range(xMat.shape[0]): nab[j] += (xMat[i,:] * ws - yMat[i]) * xMat[i,j] nab[j] /= xMat.shape[0] ws -= alpha * nab return ws xMat, yMat = loadDataSet('train_data.txt') xMat = minmaxNorm(xMat) ws = gradDes(xMat, yMat) print('Regression Weights is: ', ws) # 输出回归系数
C++梯度下降法:

#include<bits/stdc++.h> using namespace std; const double Alpha=0.5; //学习率 const int Step=3000; //迭代次数 const int N=4; //特征数 const int M=400; //训练样本数 const int testM=100; //测试样本数 double x_max[N+3], x_min[N+3]; struct Data { vector<double> x; double y; Data():x(N+1){} }; vector<Data> train,test; vector<double> w(N+1); //初始化theta void init_w() { for(int i=0;i<=N;i++) w[i]=0; } //归一化处理 void minmaxNorm(vector<Data>& dataSet) { for(auto &o:dataSet) for(int i=1;i<=N;i++) o.x[i]=(o.x[i]-x_min[i])/(x_max[i]-x_min[i]); } double g(const vector<double>& w,const vector<double>& x) { double res=0; for(int i=0;i<=N;i++) res+=w[i]*x[i]; return res; } double J(const vector<double>& w,const vector<Data>& dataSet) { double res=0; for(auto o:dataSet) res+=pow(g(w,o.x)-o.y,2); return res/(2.0*M); } int main() { fstream fin; fin.open("train_data.txt"); init_w(); //初始化w //读入训练样本 for(int i=1;i<=N;i++) x_max[i]=-1e15, x_min[i]=1e15; //min、max的初始化 train.clear(); for(int i=1;i<=M;i++) { Data o; o.x[0]=1.0; for(int i=1;i<=N;i++) { fin>>o.x[i]; x_max[i]=max(x_max[i],o.x[i]); x_min[i]=min(x_min[i],o.x[i]); } fin>>o.y; train.push_back(o); } fin.close(); //归一化处理 minmaxNorm(train); printf("初始的 J(w) = %.3f ",J(w,train)); for(int k=1;k<=Step;k++) { vector<double> del(N+1); for(int j=0;j<=N;j++) { del[j]=0; for(auto o:train) del[j]+=(g(w,o.x)-o.y)*o.x[j]; del[j]/=M; } for(int j=0;j<=N;j++) w[j]-=Alpha*del[j]; } printf("最终的 J(w) = %.3f ",J(w,train)); //输出每个theta的值 for(int i=0;i<=N;i++) printf("w[%d]=%.3f ",i,w[i]); printf(" "); //读入测试样本 fin.open("test_data.txt"); for(int i=1;i<=testM;i++) { Data o; o.x[0]=1.0; for(int i=1;i<=N;i++) fin>>o.x[i]; fin>>o.y; test.push_back(o); } //归一化处理 minmaxNorm(test); for(unsigned int i=0;i<test.size();i+=2) { printf("第 %d 组数据:预测值为 %.3f,实际值为 %.3f ",i,g(w,test[i].x),test[i].y); printf("第 %d 组数据:预测值为 %.3f,实际值为 %.3f ",i+1,g(w,test[i+1].x),test[i+1].y); } printf("在测试数据集上 J(w) = %.3f ",J(w,test)); }
