Note:
- All numbers (including target) will be positive integers.
- Elements in a combination (a1, a2, … , ak) must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak).
- The solution set must not contain duplicate combinations.
For example, given candidate set 2,3,6,7 and target 7,
A solution set is: [7] [2, 2, 3]
思路,对于2,从2开始,对于3,从3开始,保证不会出现322,只会出现223, 其实还是回溯法,或者说dfs,如下图所示
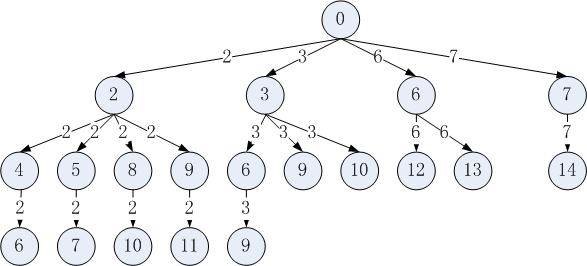
code1:在红字出剪纸,
class Solution { vector<vector<int> > m_result; public: void dfs(const vector<int> &candidates, int target, vector<int>& array, int start) { if(target < 0) return; if(target == 0) { m_result.push_back(array); return; } for(size_t i = start; i < candidates.size(); i++) { array.push_back(candidates[i]); dfs(candidates, target - candidates[i], array, i); array.pop_back(); } } vector<vector<int> > combinationSum(vector<int> &candidates, int target) { vector<int> array; sort(candidates.begin(), candidates.end()); vector<int>::iterator pos = unique(candidates.begin(), candidates.end()); candidates.erase(pos, candidates.end()); dfs( candidates, target, array, 0); return m_result; } };
code2:在红字出剪纸。
class Solution { vector<vector<int> > m_result; public: void dfs(const vector<int> &candidates, int target, vector<int>& array, int start) { if(target == 0) { m_result.push_back(array); return; } for(size_t i = start; i < candidates.size(); i++) { if(target < candidates[i]) return; array.push_back(candidates[i]); dfs(candidates, target - candidates[i], array, i); array.pop_back(); } } vector<vector<int> > combinationSum(vector<int> &candidates, int target) { vector<int> array; sort(candidates.begin(), candidates.end()); vector<int>::iterator pos = unique(candidates.begin(), candidates.end()); candidates.erase(pos, candidates.end()); dfs( candidates, target, array, 0); return m_result; } };