https://zhuanlan.zhihu.com/p/138462196
摘要:
在深度学习(deep leaming,DL)算法驱动的数据计算时代,确保算法的安全性和鲁棒性至关重要。最近,研究者发现深度学习算法无法有效地处理对抗样本。这些伪造的样本对人类的判断没有太大影响,但会使深度学习模型输出意想不到的结果。最近,在物理世界中成功实施的一系列对抗性攻击证明了此问题是所有基于深度学习系统的安全隐患。因此有关对抗性攻击和防御技术的研究引起了机器学习和安全领域研究者越来越多的关注。本文将介绍深度学习对抗攻击技术的理论基础、算法和应用。然后,讨论了防御方法中的一些代表性研究成果。这些攻击和防御机制可以为该领域的前沿研究提供参考。此外,文章进一步提出了一些开放性的技术挑战,并希望读者能够从所提出的评述和讨论中受益。
1 引言
计算能力的万亿倍增长使得深度学习(deep learning,DL)在处理各种机器学习(machine learning,ML)任务中得到广泛应用,如图像分类、自然语言处理和博弈论。然而研究者发现现有DL算法存在着严重的安全隐患:攻击者可以通过给良性样本添加特定噪声而轻易地欺骗DL模型,并且通常不会被人发现。攻击者利用人的视觉/听觉无法感知的扰动,足以使正常训练的模型输出置信度很高的错误预测,研究者将这种现象叫做对抗攻击,它被认为是在生产中部署DL模型之前的巨大障碍,因此激发了人们对对抗攻击和防御研究的广泛兴趣。
根据威胁模型可以将现有的对抗性攻击分为白盒、灰盒和黑盒攻击。这3种模型之间的差异在于攻击者了解的信息。在白盒攻击的威胁模型中,假定攻击者具有关于其目标模型的完整知识,包括模型体系结构和参数。因此攻击者可以通过任何方式直接在目标模型上制作对抗性样本。在灰盒威胁模型中,攻击者了解的信息仅限于目标模型的结构和查询访问的权限。在黑盒威胁模型中,攻击者只能依赖查询访问的返回结果来生成对抗样本。在这些威胁模型的框架中,研究者开发了许多用于对抗样本生成的攻击算法,比如基于有限内存的BFGS(limited-memory Broyden-Fletcher-Goldfarb-Shan-no,L-BFGS)、快速梯度符号法(fast gradient sign method,FGSM)、基本迭代攻击/投影梯度下降(ba-sic iterative attack/projected gradient descent,BIA/PGD、分布式对抗攻击(distributionally adversarial attack,DAA)、Carlini和Wagner(C&W)攻击、基于雅可比的显著图攻击(Jacobian-based saliency map attack,JSMA以及DeepFool。尽管这些攻击算法最初是在白盒威胁模型下设计的,但是由对抗样本在模型之间的可传递性可知:它们同样适用于灰盒威胁模型和黑盒威胁模型。本文将调查并总结对抗性攻击和防御研究领域中最前沿的研究成果。此外,我们将根据目前最新的研究进展对这些攻击和防御方式的有效性进行评述。
2 对抗攻击
以下是文中部分攻击方法的描述。
2.1 快速梯度符号法(FGSM)
Goodfellow等首先提出了一种有效的无目标攻击方法,称为快速梯度符号法(FGSM),该方法通过在良性样本的L∞范数限制下生成对抗样本,如图1所示。FGSM是典型的一步攻击算法,它沿着对抗性损失函数J(θ, x, y)的梯度方向(即符号)执行一步更新,以增加最陡峭方向上的损失。FGSM生成的对抗性样本表示如下:
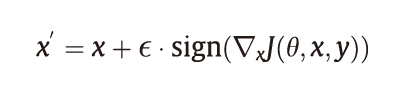
式中,ε 是扰动大小。通过降低J(θ, x, y′)的梯度(其中y′表示目标类别)可以将FGSM轻松地扩展为目标攻击算法(targeted FGSM)。如果将交叉熵作为对抗损失,则此更新过程可以减少预测概率向量和目标概率向量之间的交叉熵。目标攻击算法的梯度更新可以表示为:
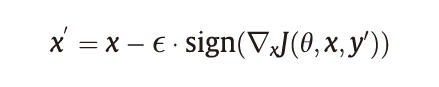
此外,在良性样本上先添加随机扰动再执行FGSM可以提高FGSM生成对抗样本的性能和多样性。
2.2 基本迭代攻击和投影梯度下降
Kurakin等提出了BIA方法,该方法通过将一个迭代优化器迭代优化多次来提高FGSM的性能。BIA以较小的步长执行FGSM,并将更新后的对抗样本裁剪到有效范围内,通过这样的方式总共T次迭代,在第k次迭代中的梯度更新方式如下:
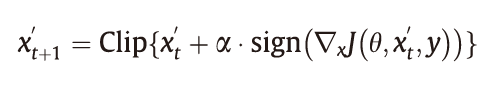
式中,αT = ε。投影梯度下降(PGD)可以看作是BIA的广义形式,这种方法没有约束αT = ε。为了约束对抗性扰动,PGD将每次迭代学习的对抗性样本投影到良性样本的ε- L∞邻域中,从而使对抗性扰动值小于ε。其更新方式如下:
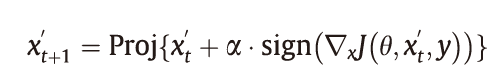
式中,Proj会将更新后的对抗样本投影到ε- L∞邻域和有效范围内。
2.3 动量迭代攻击(momentum iterative attack)
受动量优化器的启发,Dong等提出将动量记忆集成到BIM的迭代过程中,并推导了一种新的迭代算法Momentum Iterative FGSM(MI-FGSM)。该方法通过以下方式迭代更新其对抗样本:
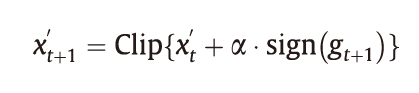
式中,梯度gk+1通过gk+1 = μ·gk + Δx J(θ,xk',y)/|| Δx J(θ,xk',y)||1更新。文献提出的方案是以一组集成模型为目标,在黑盒/灰盒设置下攻击一个不可见的模型。其基本思想是考虑多个模型相对于输入的梯度,并综合确定一个梯度方向,这种攻击方法生成的对抗样本更可能转移攻击其他黑盒/灰盒模型。MI-FGSM与集成攻击方案的结合在NIPS 2017无目标攻击和度量攻击竞赛(黑盒设置)中获得了第一名。
2.4 Carlini 和Wagner 攻击
Carlini和Wagner提出了一组基于优化的对抗攻击C&W,它们可以生成L0、L2和L∞范数限制下的对抗样本CW0、CW2和CW∞。与L-BFGS类似,将优化目标函数表示为:
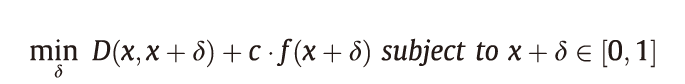
式中,δ 是对抗扰动;D(∙,∙)表示L0、L2或L∞距离度量;f(x +δ)是自定义的对抗损失,当且仅当DNN的预测为攻击目标时才满足f(x +δ)≤0。为了确保x +δ产生能有效的
图像(即x +δ ∈ [0, 1]),引入了一个新变量来代替δ,如式(11)所示:
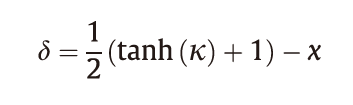
这样,x +δ =1/2(tanh(k) + 1)在优化过程中始终位于[0, 1]中。除了在MNIST、CIFAR10和ImageNet的正常训练DNN模型上获得100%的攻击成功率外,C&W攻击还可以破坏防御性蒸馏模型,而这些模型可以使L-BFGS和Deepfool无法找到对抗性样本。
2.5 通用对抗攻击
上述所有攻击都是针对良性样本来精心设计对抗性扰动的。换句话说,对抗性扰动不会在良性样本之间传递。因此一个自然的问题是:是否存在一种普遍的扰动会欺骗大多数良性样本的网络?在每次迭代中,对于当前扰动无法欺骗的良性样本,将求解一个类似于L-BFGS的优化问题,以找到危害这些样本所需的最小附加扰动。附加扰动将添加到当前扰动中。最终,扰动使大多数良性样本欺骗了网络。实验表明,这种简单的选代算法可以有效地攻击深度神经网络,如CaffeNet、GoogleNet、VGG和ResNet。出乎意料的是,这种可在不同样本中传递的扰动同时可以应用到其他不同的模型中,例如,在VGG上制作的通用扰动在其他模型上也可以达到53%以上的欺骗率。
3 对抗防御
3.1 对抗训练
对抗训练是一种针对对抗样本的直观防御方法,该方法试图通过利用对抗样本进行训练来提高神经网络的鲁棒性。从形式上讲,这是一个Min-Max的游戏,可以表述为:
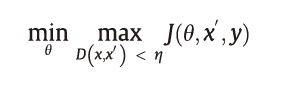
式中,J(θ, x′, y)是对抗损失函数;θ是网络权重;x′是对抗输入;y是标签真值。D(x, x′)表示x和x′之间的某种距离度量。内部的最大化优化问题是找到最有效的对抗样本,这可以通过精心设计的对抗攻击实现,如FGSM和PGD。外部的最小化优化问题是损失函数最小化的标准训练流程。最终的网络应该能够抵抗训练阶段用的生成对抗性样本的对抗性攻击。最近的研究表明:对抗性训练是对抗性攻击最有效的防御手段之一。主要是因为这种方法在几个基准数据集上达到了最高的精度。因此在本节中,我们将详细介绍过去几年里表现最好的对抗训练技术。
FGSM 对抗训练:Goodfellow等首先提出用良性和FGSM生成的对抗样本训练神经网络以增强网络其鲁棒性的方法。他们提出的对抗目标函数可以表达为:
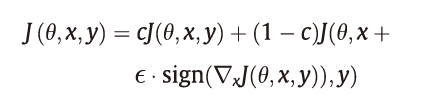
式中,x +ϵsign( ΔxJ(θ, x, y))是良性样本x根据FGSM方法生成的对抗样本;c是用于平衡良性和对抗性样本的准确性。文献中的实验表明,该网络对于FGSM方法生成的对抗性样本变得有些健壮。具体来说,在对抗训练中对抗样本的错误率从89.4%急剧下降至17.9%。尽管该方法对FGSM的攻击有效,但是训练后的模型仍然容易受到基于迭代/优化方式的对抗攻击。因此许多研究进一步挖掘了具有更强对抗性攻击(如BIA/PGD攻击)的对抗性训练。
3.2 随机化
最近的许多防御措施都采用随机化来减轻输入/特征域中对抗性扰动的影响,因为从直觉上看,DNN总是对随机扰动具有鲁棒性。基于随机化的防御方法试图将对抗性效应随机化为随机性效应,当然这对大多数DNN而言都不是问题。在黑盒攻击和灰盒攻击的设置下,基于随机化的防御获得了不错的性能,但是在白盒攻击下,EoT方法能够通过在攻击过程中考虑随机过程来破坏大多数防御方法。本节将详细介绍几种基于随机化的代表性防御方式,并介绍其针对不同环境中各种防御的性能。
3.3 去噪
就减轻对抗性扰动/效果而言,降噪是一种非常简单的方法。之前的工作指出了设计这种防御的两个方向,包括输入降噪和特征图降噪。其中第一个方向试图从输入中部分或完全消除对抗性扰动,第二个方向是减轻对抗性扰动对DNN学习高级功能的影响。本节将详细介绍这两个方向上的几种著名防御方法。
3.4 可证明式期伸
以上所有介绍的防御都是启发式防御,这意味着这些防御的有效性只在实验上得到验证,而没有在理论上得到证明。如果无法计算理论上的错误率,这些启发式防御可能会被未来的新攻击所打破。因此许多研究者致力于探索可证明的防御方法,在一类定义明确的攻击下,这些方法始终能保持一定的准确性。本节将介绍几种具有代表性的可证明的防御。
3.5 基于贝叶斯模型的防御
Liu等将贝叶斯神经网络(Bayesian neural network,BNN)与对抗训练相结合,从而学习在对抗攻击下的最优模型的权重分布。具体来说,作者假设网络中的所有权重都是随机的,并使用BNN理论中常用的技术训练网络。通过对抗性训练,这种随机的BNN,与RSE和CIFAR10以及STL10和ImageNet143的常见的对抗性训练相比,显著提高了对抗鲁棒性。Schott等建议基于贝叶斯模型对输入数据的分类条件分布进行建模,并将新样本分类为相应类别条件模型产生最高似然性的类别。他们将模型命名为Analysis by Synthesis model(ABS)。ABS被称为MNIST数据集上针对L0、I2和L∞。攻击的第一个健壮模型。ABS在抵抗L0和L2攻击方面达到了最先进的性能,但在L∞的攻击下其性能要比PGD对抗训练的模型稍差。
4 讨论
4.1 白盒与黑盒攻击
从攻击者的角度来看,白盒攻击和黑盒攻击的主要区别在于它们对目标模型的访问权限。在白盒攻击中,攻击者可以访问模型的结构和权重,以便他们可以通过文献中的方法计算真实的模型梯度或近似梯度,此外攻击者还可以根据防御方法和参数调整其攻击方法。在这种情况下,以前引入的大多数启发式防御实际上无法抵御这种强大的自适应攻击者。在黑盒攻击中,模型结构和权重不会被攻击者知道,在这种情况下,为了使用上述基于梯度的攻击算法,对手必须从有限的信息中推断出模型的梯度。在没有任何特定模型信息的情况下,对模型梯度的无偏估计就是对具有不同随机种子的一组预训练模型梯度的期望。文献使用基于动量梯度的方法进行此梯度估计,并在NIPS2017挑战赛(在黑盒设置下)中获得第一名。Chen等研究了另一种黑盒攻击方法,该方法可以向攻击者授予额外的查询访问权限。因此如果给定精心设计的输入,攻击者可以从目标模型的输出推断出梯度。在这种设置下,可以应用零阶方法来更好地估计模型梯度。但是此方法的缺点是需要进行大量的查询操作,其查询量与数据维度成比例。
4.2 对抗攻击与防御研究趋势之间的差异
对抗攻击的研究趋势主要包括两个方向。第一个是设计更有效、更强大的攻击用来评估新兴的防御系统,这个方向的重要性很直观,因为我们希望在潜在对手面前预先了解所有的风险。第二个是实现物理世界中的对抗攻击。以前对该研究主题的主要疑问是那些对抗性攻击是否会对物理世界形成真正的威胁。一些研究人员怀疑由于某些环境因素的影响,最初在数字空间中设计的对抗性攻击将无效。Kurakin首先通过使用模型梯度相对于输入的期望值并加上环境因素引起的随机噪声来实现物理世界中的对抗攻击。Ekholt等进一步考虑了掩膜和制造误差,从而实现了交通标志的对抗性扰动。最近Cao等成功生成的对抗目标可以用来欺骗基于激光雷达的检测系统,这些都验证了物理对抗样本的存在。在防御方面,由于大多数启发式防御都无法防御自适应白盒攻击,因此研究者开始关注可证明的防御,这种防御是指无论攻击者采用哪种攻击方式,可证明防御都可以在一定程度下保证防御的性能。但是到目前为止,可扩展性是目前大多数可证明防御所普遍具有的问题。例如,区间界分析是最近流行的证明式防御方法,但是它不能扩展到非常深的神经网络和大型数据集。由此可见,与攻击相比,防御系统的发展面临着更多的挑战。这主要是因为一次攻击只能针对一类防御,所以防御机理急需被证明,这样某种防御在某些情况下对所有可能的攻击才能都是有效。
4.3 未解决的主要挑战
(1)对抗样本背后的因果关系。虽然提出了许多对抗攻击方式,但是对抗样本的因果关系仍不清楚。早期对这一问题的研究将对抗样本的出现归功于模型结构和学习方法,研究者认为适当的策略和网络结构将显著提高对抗样本的鲁棒性。研究者沿着这种思路尝试过一些探索,特别是与产生模糊梯度相关的研究,然而实际上这可能是一种不太合理的研究方向。相反,最近的研究发现对抗性的出现更可能是高维数据几何和训练数据不足的结果。具体来说,有关文献还证明了对抗性扰动在几个概念验证数据集(如{0,1}和同心n维球体)上按比例放缩。Ludwig等表明对抗性强的任务比普通的ML任务需要更多的数据,并且所需的数据大小可能以比例O(√1/d)放缩。
(2)通用鲁棒决策边界的存在。由于在不同度量标准下定义了许多对抗攻击方法,一个自然的问题是是否存在由特定训练策略的某种DNN来学习的通用鲁棒决策边界。当前,这个问题的答案是“否”。尽管PGD对抗训练对各种L范数。攻击表现出显著的抵抗力,但有文献表明它仍然容易受到其他。范数的对抗攻击,如EAD和CW2。Khoury等证明了2-同心球面数据集的最优I2和L。决策边界是不同的,它们的差异随着数据集的共维(即数据流形的维数与整个数据空间的维数之差)而增大。
(3)有效防御白盒攻击。我们仍然没有看到一种能够很好地平衡效果和效率的防御。在有效性方面,对抗性训练表现出最好的性能,但计算成本很高。在效率方面,许多基于随机和去噪的防御/检测系统的配置只需几秒钟。然而,最近的许多论文表明这些防御方法并没有他们声称的那样有效。这些研究可证明防御理论为实现对抗防御指明了一条道路,但其准确性和有效性都远远不能满足实际要求。