一、定义
前言
顾名思义,快速排序是实践中的一种快速排序算法,在C++或对Java基本类型的排序中特别有用。它的平均运行时间是(O(NlogN))。该算法之所以特别快,主要是由于非常精炼和高度优化的内部循环。它的最坏性能(O(N^2))。通过将堆排序和快速排序的结合,由于堆排序的最坏情形是(O(NlogN)),可以对几乎所有的输入都能达到快速排序的快速运行时间。
Java的基本类型本身是由C语言继承过来,所以它的结构是直接存储值而不是引用。所以用归并排序明显不合适,因为归并排序产生的数组和拷贝,对值的操作会耗费大量时间。对Java的引用反而更好,因为引用的拷贝不涉及到内存的处理。所以Java的基本类型使用快速排序,而引用类型使用归并排序。
排序过程
描述
对于数组S的排序过程:
- 如果S中元素个数是0或者1,则直接返回。
- 取S中任意元素(v),称之为枢纽元(pivot)。
- 将(S-{v})和S中其余元素划分成2个不相交的集合:(S_1 = {xin S-{v} | x leq v })和(S_2 = {xin S-{v} | x ge v })。
- 返回{quicksort( (S_1))后跟(v),继而返回quicksort($S_2 $)}。
或者 :
- 在S中随意位置选择一个元素(v),作为枢纽元。假设下标为(i),值为(x)。
- 将S从(i)分为前后两部分。
- 将值小于(x),的元素放在 (i) 前面,将值大于(x),的元素放在 (i) 后面。
- 递归排序,得到有序数组。
选取枢纽元
看上述描述,枢纽元的作用在于:做一个比较的标杆,并根据这个标杆将数组分为前后两部分,所以,理想的枢纽元是中间值,但是一个随机数组,不可能一下找到中间值。那么如何选择枢纽元是很关键的。
坏的枢纽元:最大值或者最小值,当我们不小心选取了最大值或者最小值作为枢纽元,那么很明显,我们无法将其分为2部分,这里提供一种常用的枢纽元选择法:三数中值分割法。
三数中值分割法
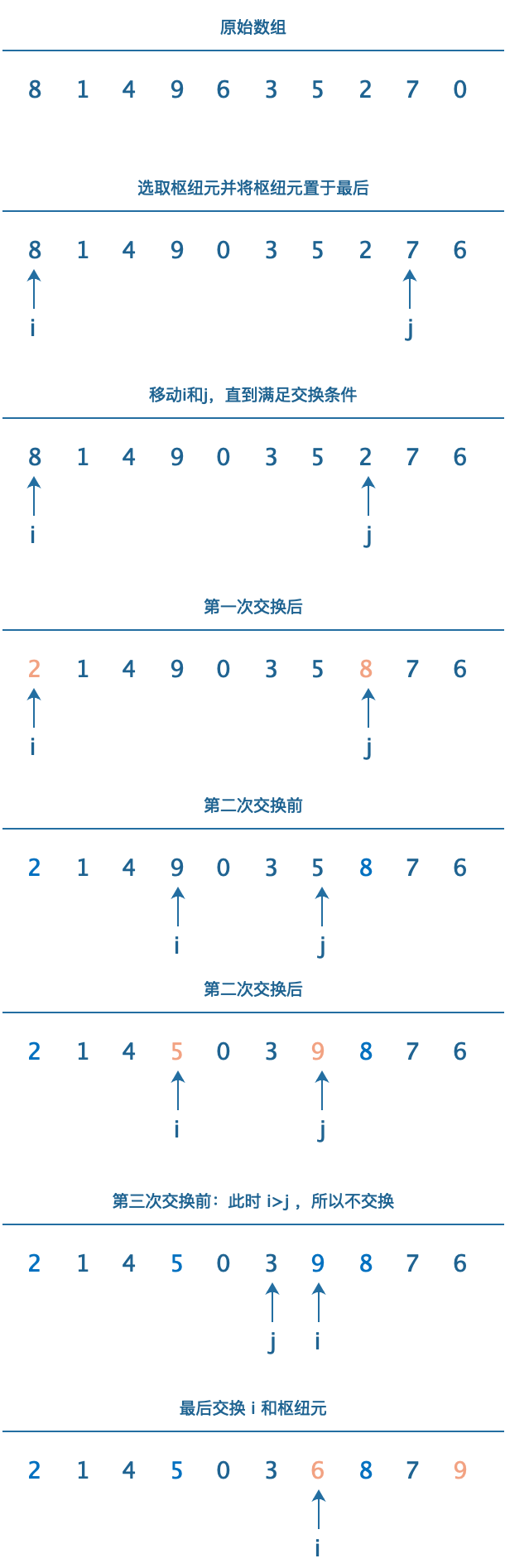
在一个N的数组中,使用左端,右端和中心三个位置上的元素的中值作为枢纽元。例如,输入为8,1,4,9,6,3,5,2,7,0。它的左端是8,右端是0,中心位置是6,我们在这三个值中选择中值。所以枢纽元为6。
分割策略
分割策略很多种,此处描述的策略被证明能够给出最好的结果。
- 通过将枢纽元与最后的元素交换使得枢纽元离开要被分割的数据段。
- 分别使用(i) 和(j) 作为标示,(i)从第一个元素开始,(j) 从倒数第二个元素开始。
- 当(i) 在(j) 的左边时,我们将(i) 向右移动,而(j) 向左移动。
- 当(i) 和(j) 停止时,(i) 指向的元素比枢纽元大,而(j) 指向的元素比枢纽元小。
- 交换(i) 和(j) 指向的元素的值。
- 继续移动(i) 和(j) 直到(i) 和(j) 交错为止。
- 最后将(i) 指向的元素和枢纽元交换。
图解:
图解说明:
最后一步枢纽元和(i)交换值之后,我们可以分析得到位置(p< i)的值都小于枢纽元,(p>i)的值都大于枢纽元。这样我们就将数组以枢纽元为单位区分为两部分,前部分小于枢纽元,后部分大于枢纽元。
这是描述第一次分割,而后我们可以:对前部分再进行分割,对后部分进行分割。一直到所有元素有序!没错,就是需要用递归!
优化
此处我们可以发现,有一步明显存在优化的可能。即:选择枢纽元并将枢纽元放到数组最后。因为我们枢纽元是选择的三数中值,意味着,我们可以对(i=0,i=n-1,i=n/2) 三个元素进行排序。所以我们可以考虑将比枢纽元大的值放在最后,比枢纽元小的值,放在第一位,最后将枢纽元与倒数第二个值交换,如下图:

这样优化,可以减少比较次数。
二、算法分析
很明显,按照上述过程,快速排序也是递归进行的。
最好时间
对于类似分割递归的时间,其实我们如果运气好,每次选择的枢纽元都可以将数组分为2部分,那么它的时间明显可以为
此过程推导很简单,利用相加消除(其实跟归并排序完全相同)。得到:
平均情况
对于平均情况,根上述最好时间是类似的分析。只不过不能每次都正好分为2部分,也就是不能使用(2T(N/2)),而是随机求和。我们可以分为前部分为1,后部分为N-1。前部分2,后部分N-1….之类的,可以知道,一共有N/2种组合。每个部分的大小可能性为2/N。所以得到:
同样利用相加消除:得到
这个推导过程还是可以参考归并排序。
代码地址
https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterSeven/QuicksortEx.java