注:本蒟蒻只得了100分,那些想通过看这篇文章得到200分的同学可以溜了喔

这个题一开始没什么思路,只是听之前A过的大佬说这题是什么最长上升子序列最长不上升子序列巴拉巴拉什么玩意儿的
那时候菜听不懂 虽然现在也菜 然后我去看了洛谷网课发的ppt上面讲的最长上升子序列(跟最长不上升子序列是差不多的啦)
其实也没太看懂。。(qwq了炸菜的真我
但是后来想想其实是一个很简单的思路:当前的数的最长不上升子序列=之前的每一个大于它的数中最长的不上升子序列+1 |或者| 当前的数的最长不上升子序列=当前的数的不上升子序列
(取最大的那个就可以
这个思路就像一堆嫌贫爱富的小同学找朋友一样:很多个小同学排成一排,他们都喜欢跟最有钱的人成为朋友,找到了朋友那个朋友的钱财就属于他们两个的了(当然他自己的钱不属于那个朋友),并且如果以后有人选择他做朋友,那么他朋友的钱也是他另一个朋友的钱(他的朋友骂骂咧咧的走了),而且那个朋友年龄还必须比他大(大孩子会照顾人欸),不然再有钱他们俩也不会成为朋友的(毕竟小孩子比较小气,不肯跟朋友分享自己的软妹币)。可是他们只能知道自己之前的孩子的钱数以及岁数,所以他们要开始一个一个比较看看哪一个最适合当他的朋友。小花今年14岁了,现在他该选朋友了。他首先来到靠着他最近的一个小朋友问:“你多少岁啊?” 那个小朋友说:“我今年12岁了!”小花想:这个小朋友比我小,他肯定不会把他的软妹币分给我!那我就继续往前走吧。小花来到他前面第二个小朋友(就先叫他小明吧)面前问:“你今年多少岁哇?”小明说:“我今年18岁了!”小花想:这个小朋友比我大,大孩子肯定大方,那我就跟他做朋友吧!于是他们两个成为了要好的朋友。可是小花又想了:万一前面还有小朋友比我大,而且比小明富有可怎么办啊??那我先让小明把他的软妹币分给我,我再往前找找看,如果有比小明更富有的就抛弃小明把(话说你怎么这么不要脸啊喂!!!),于是小花继续往前走......最终小花遇到了一个年龄跟他一般大而且极其富有的小朋友,于是他们幸福快乐的生活在了一起(bushi)......于是小花拿了这个小朋友的钱就走了(太不要脸了真的是)。
说起来这么麻烦其实就是一行代码啦:t[i]=max(t[i],t[j]+1);(j<i)
然后就是这么简单,这是代码,最后输出maxx就ok啦(a数组是存数的):
for(int i=0;i<n;i++){//遍历每一个数 for(int j=i-1;j>=0;j--){//遍历每一个小于i的数 if(a[j]>=a[i]){//如果当前的数符合条件(即找到了一个大于等于a[i]的数 t[i]=max(t[i],t[j]+1);//动态转移方程,刚才解释过了 } } } for(int i=0;i<n;i++){//遍历t数组 maxx=max(maxx,t[i]);//取最长的不上升子序列 t[i]=1;//一会还要用,所以要初始化 }
关于初始化我要说明一下,为什么要让t数组的最长不上升子序列的值都初始化为1呢?因为每一个数都可以看作为一个开始的数。不是每次都会让t[i]的值更新吗?t[j]+1肯定会大于等于t[i]啊,为什么还要费这么多事?因为我们还加了一个特判条件a[j]>=a[i],如果a[j]<a[i]这一条就不会被执行到了,我们下次如果要用到这个数,他的最长上升子序列就会少个1。当然你在if后面加一个else然后让t[i]=1也是可以的,可是那样就很麻烦了。看你心情咯
然后我们再看第二个输出,理解起来可能有点麻烦,但其实就是让你找到最少并且可以覆盖整个数列的最长不上升子序列。
听起来好麻烦哦。。。而且毫无思路
于是我查啊查啊终于知道了一个很神奇的东西:Dilworth定理
他是一个可以让我们A题的关键,所以我满怀期待取百度了一下这个陌生的词:
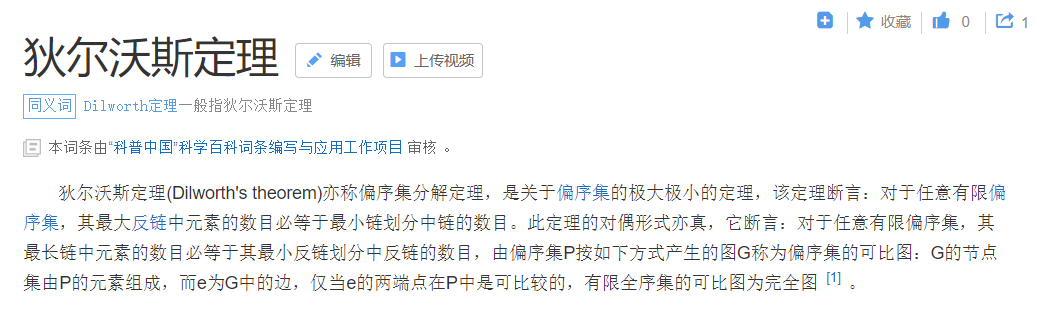
行吧,是我卑微了(看不懂就很好
但是为了让大家理解这个定理,我找到了一个更通俗易懂的说法:

是不是感觉清楚多了??
代码实现也不难,直接把上面的代码复制粘贴过来把>=改成<就ok啦
不过这里有一个我们需要咬文嚼字的地方:最长不上升子序列&最长上升子序列
最长不上升子序列:只要不上升,下降或者相等也可以
最长上升子序列:必须上升
这就是为什么我们在改的时候不改成<=
最终代码放一下:
#include<iostream> #include<cstdio> using namespace std; int n,a[100010],t[100010],ans=0,maxx=0,minn=0; int main(){ while(scanf("%d",&a[n])!=-1){//无限输入,不会的可以复制一下啦(其实我也是在小姐妹那里求来的qwq) t[n]=1;//千万不要忘了初始化!!! n++;//看这些数一共有多少个 } t[0]=1; for(int i=0;i<n;i++){ for(int j=i-1;j>=0;j--){ if(a[j]>=a[i]){ t[i]=max(t[i],t[j]+1);//动态转移方程 } } } for(int i=0;i<n;i++){ maxx=max(maxx,t[i]);//求最长不上升子序列 t[i]=1;//再次初始化 } for(int i=0;i<n;i++){ for(int j=i-1;j>=0;j--){ if(a[j]<a[i]){ t[i]=max(t[i],t[j]+1);//依然是动态转移方程 } } } for(int i=0;i<n;i++){ minn=max(minn,t[i]);//求最长上升子序列 } printf("%d %d ",maxx,minn);//输出 return 0; }