AC算法(Actor-Critic算法)最早是由《Neuronlike Adaptive Elements That Can Solve Difficult Learning Control Problems Neuronlike Adaptive Elements That Can Solve Difficult Learning Control Problems》论文提出,不过该论文是出于credit assignment problem设计了actor部分和critic部分,其中critic对actor获得的reward进行credit assignment 处理和学习,然后把处理后获得的新reward传递给actor进行学习,这样结合了critic和actor两部分学习器,得到了一个更优的学习器。
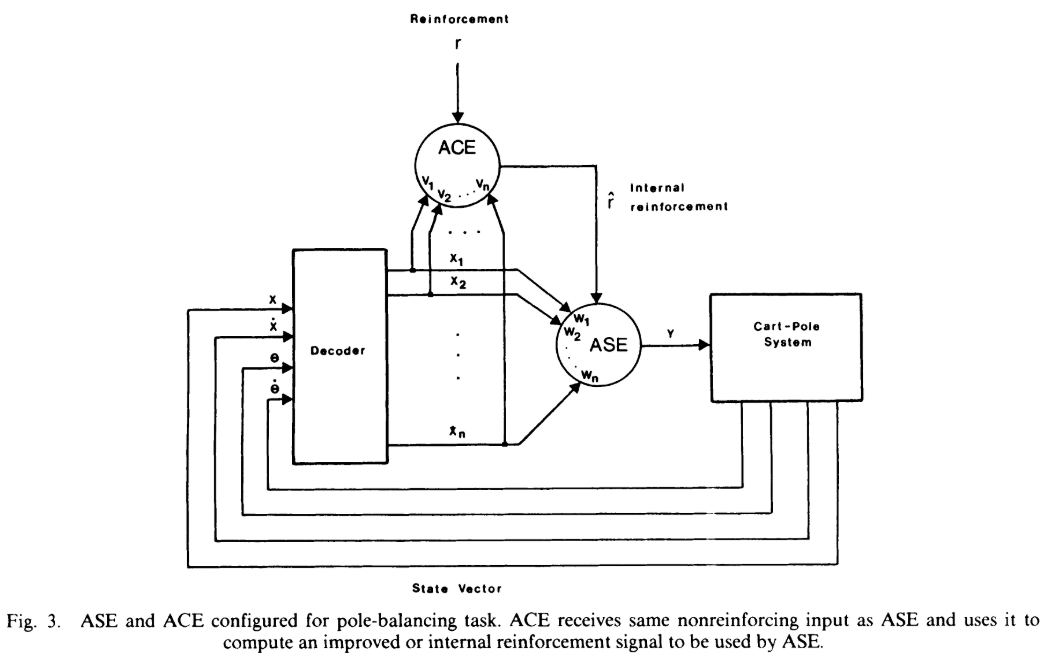
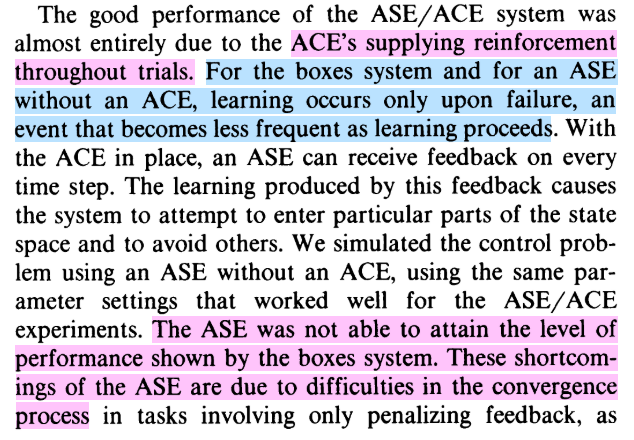
可以看到最初的AC算法只是为了更好解决credit assignment问题,将Actor和Critic两者结合,其中的Critic主要就是为每一步的actor学习给出一个更好的credit assignment的reward。最初的AC算法中critic更多的是在辅助actor来进行学习的,可以看到现在的AC算法除了保留了将两个学习器结合的思想以外已经与最初的AC算法差距较大了,而现在的AC算法形式为论文《Policy Gradient Methods for Reinforcement Learning with Function Approximation》给出的。
因此,本文主要讨论的是对论文《Policy Gradient Methods for Reinforcement Learning with Function Approximation》的一些理解。前几天写过一个该论文的一些基本形式和证明(
论文《policy-gradient-methods-for-reinforcement-learning-with-function-approximation 》的阅读——强化学习中的策略梯度算法基本形式与部分证明
),所以本文算是一个补充版,或是后续版。
---------------------------------------------------------
首先给出论文《Policy Gradient Methods for Reinforcement Learning with Function Approximation》中的定理1:
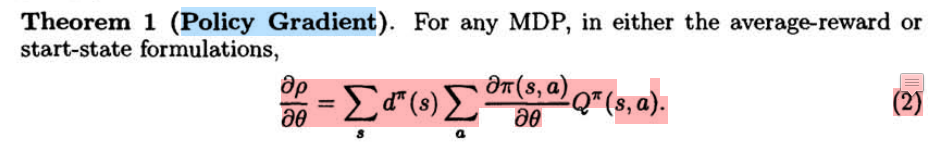
定理1 又被称作是策略梯度定理,可以说强化学习中的策略梯度一类的算法基本都是基于这个定理来进行构建的。由于前文对该定理给出了一些解释,这里就不具体解释了。
本文的重点是讲一下对论文中定理2的一些理解, 下面给出定理2及其前提设定:

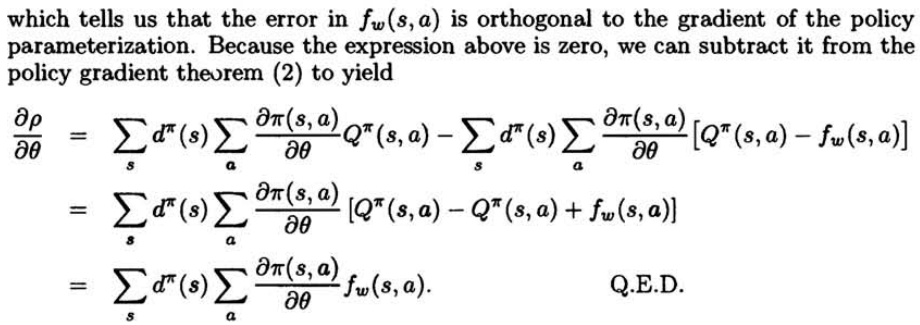
上面的内容比较长,可以说公式(3)和(4)是对定理2的前提设定,也就是说定理2是假设在满足公式(3)和(4)的前提条件下进行推导的。
由公式(3)和(4)我们可以推导出定理2的表现形式,即公式(5)。其中公式(6)及以下为对定理2的表现形式(即公式(5))进行的证明过程。
公式(3)的意思是说,满足公式(3)的话,f(s,a) 对 Q(s,a)的估计为收敛于局部最优,换句话说就是:公式(3)是 f(s,a) 对 Q(s,a)的估计收敛于局部最优的表现形式。假设公式(3)成立则说明 f(s,a) 对 Q(s,a)的估计是假设收敛于局部最优的。
公式(4)则是假设f(s,a)对参数w的微分等于log(pi(s,a)) 对参数theta的微分。
在公式(3)和(4)成立的前提下,才得到定理2 的表现形式(公式5),也就是说定理2是在讲满足公式(3)和(4)的前提下才可以用f(s,a)替代Q(s,a)来对策略的表现求梯度(即定理1)。
刚开始看到定理2的时候感觉多此一举,直接用一个函数来近似表示Q(s,a)不就可以了吗,为什么还要假设满足公式(3)和(4)。研究了些时间才有所了解,如果不满足公式(3),那么f(s,a)对Q(s,a)的估计是没有限定的,也就是说f(s,a)是不能很好的来估计Q(s,a)的,所以我们要加入公式(3)作为前提。或者说只有满足了公式(3)才能说f(s,a)是对Q(s,a)的很好的估计,因为此时的估计函数f(s,a)是收敛于局部最优的。
那么公式(4)又是为何呢,它又起到什么作用呢?
个人理解:
即使满足了公式(3),f(s,a)是对Q(s,a)的一个很好的估计(收敛于局部最优),也不能说f(s,a)就一定可以替换定理1中的Q(s,a)。因为毕竟f(s,a)并不正在等于Q(s,a),只能说在(s,a) 这个(状态,动作 对)分布的情况下,f(s,a)与Q(s,a)的差值平方在(s,a)分布的情况下的期望对参数w的导数为0,因为毕竟 f(s,a) 对Q(s,a)的估计还是难免会存在误差的。
在不考虑公式(4)的情况下,我们只能说下面的公式是成立的:

但是对于公式(6),即下面公式,是难以使其成立的。

也或者说下面公式是难以成立的:
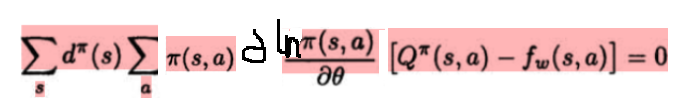
----------------------------------------------
以上对公式(3)和(4)的一个理解就是,如果只满足了公式(3)只能说明f(s,a)对Q(s,a)的估计收敛于局部最优,而只有同时满足公式(4)的收敛于局部最优的f(s,a)才能很好的替换定理1中的Q(s,a)。
当然,在实际应用中公式(3)和公式(4)都是难以满足的,或者说论文中的定理1和定理2是纯理论假设推导,是在一种很理想化的情况下才会成立。
公式(3)的表现形式我们可以假设策略固定不变,然后在固定策略的前提下一直训练f(s,a)使其对Q(s,a)的估计收敛于局部最优,而此时所得到的f(s,a)并不一定会满足公式(4)。而只有满足公式(4)的收敛于局部最优的f(s,a)才满足定理2,才可以替换定理1中的Q(s,a)。
现在的常用函数一般为深度神经网络,也就是说f(s,a)和pi(s,a)一般也是用深度神经网络来表示的,现在常用的对f(s,a)进行更新的方法一般可以较好的使f(s,a)对Q(s,a)的估计收敛,至于能否收敛于局部最优就难以保证了,而对于公式(4)中的限定现在也是基本没有见过哪个具体算法对其进行限定的。
可以说对公式(3)基本可以实现部分满足(使其收敛,不保证收敛于局部最优),而对于公式(4)的限定实际算法一般不做处理。
----------------------------------------------------