前情提要:
取自:http://news.ifeng.com/a/20170515/51093579_0.shtml
值函数估计

离散状态下可以用表格来表示值函数或策略;但进入连续状态空间就要用一个函数的近似来表示,这个方法叫做值函数近似。
比如,我们可以用一个线性函数来表示,V值是表示状态s下面的一个值,状态s先有一个特征的向量φ(s),这个V值表达出来就是一个线性的参数乘以特征的内积。Q值里面有一个动作,假设这个动作是离散的,一种方式是把这个动作和状态放在一起变成一个特征,另一种方法是给每一个动作单独做一个模型。
但我们现在先不管那些问题,先看做了近似以后怎么来学?我们想知道的是,这里的Q值,是希望Q值近似以后,够尽量逼近真实的Q值。如果已经知道真实的Q值,怎么逼近呢?最简单的方法就是做一个最小二乘回归。其中一种解法是求导。求导以后,导数表示为,真实的Q和估计的Q的差值,然后再乘对Q值模型的导。可以看到,导数表达的含义与之前的模特卡罗误差、TD误差是一致的,只不过更新的是参数w。把这种更新方式套进Q-learning里,其他地方都没有变,只得到了用值函数逼近的Q-Learning方法。

用批量学习改进
还有一些改进的方式。比如说我们在训练近似模型的时候,在一个样本上训练可能会不稳定,所以可以用Batch Models的方式,积累一批数据来训练这个模型。

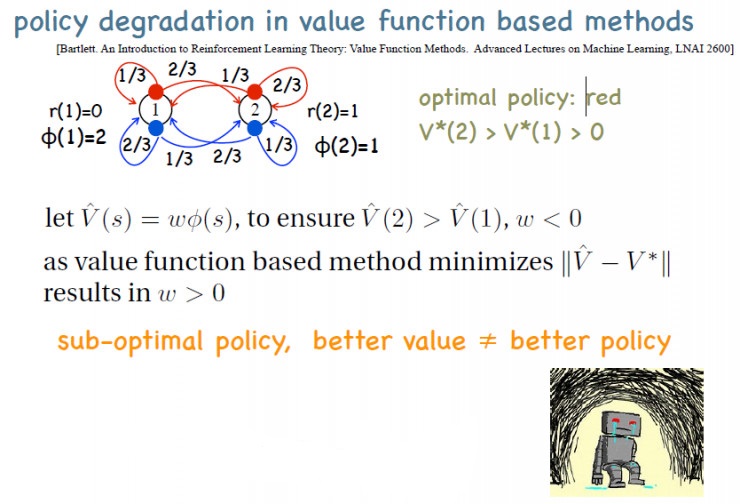
但是用值函数估计会有一个问题——这种方法可以收敛到最优策略,但前提必须是用表格的表达方式;如果用的是函数近似,则会出现策略退化,即对Q值估计越大,策略越差。
举一个简单的例子,现在有两个状态,一个是状态1,一个是状态2,状态1的特征为2,状态2的特征为1。我们设定奖赏,使得状态2的最优V值比状态1的要大。这时如果用一个线性函数来表示这个V,也就是用W乘以特征,这个特征只有一维,最优的这个V值2是比1大的,1的特征值要高一点,2的特征值要小一点,所以最优的W就应该是个负数,这样会使得V(2)比V(1)大,因而能导出最优策略。
但是基于值函数的做法是要使得V值尽量靠近最优的V值,最优的V值又是正值,这样会导致这个W一定是正的,无法得到最优的策略。这样值函数估计得越准,策略越差的现象被称为策略退化。
====================================================================
以上这个小例子已给出在一种模型情况下最优策略和值函数,具体参看如下:
https://www.cnblogs.com/devilmaycry812839668/p/10314049.html
超参数设置: gama折扣因子都为0.99 , 两浮点数相同的判断规格都为0.0001 。
可知, 在折扣因子 gama 设置为0.99的情况下, 状态“1”的状态值为66.65674655343062,
状态“2”的状态值为66.65674655343062 。
可以发现 真实的状态值在计算后居然得出了 两个状态值相同的结果,这个和本文上面所引用到的内容貌似不符,个人观点可能是因为这两个状态采取动作后所跳转新状态后得到的奖励值过小,奖励值差距也过小,所以经过多轮的迭代学习发现得出了两个状态相同的值函数的结果。
不过又研究一下发现好像也不是这个原因:
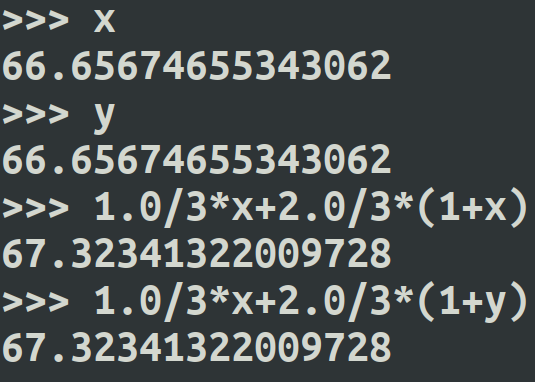
这里1状态V值为x, 2状态V值为y, 状态1 采取最优动作后再次估计状态值为 1.0/3*x + 2.0/3*(1+y)
状态2 采取最优动作后再次估计状态值也为 1.0/3*x + 2.0/3*(1+y)
最后状态1和2再次更新得到的状态值仍然相同为 67.32341322009728, 所以上部分所说的状态2的值大于状态1的值是错误的,这两个状态值本就应该相同。
============================================================
在动态规划问题中我们一般认为模型是已知的,也就是说我们知道agent执行某个动作后跳转到哪个状态的概率为多少,会获得多少reward。
而在强化学习中我们一般认为模型是未知的,也就是说我们需要自己去构建一个算法去识别出在某一状态时我们应该选择什么样的动作,即寻找策略。因此我们一般采用模拟采样的方法,如:蒙特卡洛法,但是由于该方法采样需要每一次都是完整的决策过程,然后对其过程中动作值进行更新,因此我们一般采用时序差分法,如:Q-Learning 和 Sarsa 。
本文内容:
1. 基于单个样本的 值函数估计强化学习方法例子 (最小二乘估计)( Q-learning 和 Sarsa )
其中, Q-Learning 代码如下:
#encoding:UTF-8 #!/usr/bin/env python3 import random #动作 actions=[0, 1] #状态 states=[1, 2] #构建环境 s, a r s a def next_state_reward(state, action): alfa=random.random() if state==1: if action==0: if alfa<=1.0/3: new_state=1 reward=0 else: new_state=2 reward=1 else: if alfa>1.0/3: new_state=1 reward=0 else: new_state=2 reward=1 else: if action==0: if alfa<=1.0/3: new_state=1 reward=0 else: new_state=2 reward=1 else: if alfa>1.0/3: new_state=1 reward=0 else: new_state=2 reward=1 return new_state, reward import torch.nn as nn import torch.optim # 构建模型 # 最小二乘法 # 输入状态1维 输出action_q值2维(两个动作) model = nn.Sequential( nn.Linear(1, 2), ) #反传优化器 optimizer = torch.optim.Adam(model.parameters()) epsilon=0.4 def act(model, state, act_type="greedy", epsilon=epsilon): if (act_type!="greedy") or (random.random() > epsilon): # 选最大的 q_value = model.forward(state) action = q_value.max(1)[1].item() else: # 随便选 action = random.randrange(len(actions)) return action gama=0.99 learning_rate=0.1 def q_learning(): state=random.choice(states) # 单个状态变为序列型数据 state=(state, ) state = torch.FloatTensor(state).unsqueeze(0) action=act(model, state, act_type="greedy") # q 值 qs = model(state) # 单个数据 位置为0 q_value = qs[0][action] # 下一状态 和 奖励 next_state, reward=next_state_reward(state, action) # 单个状态变为序列型数据 next_state=(next_state, ) next_state = torch.FloatTensor(next_state).unsqueeze(0) # 选择的下一动作 next_action=act(model, next_state, act_type="max") # q 值 next_q_value, _ = model(next_state).max(1) q_estimate = reward + gama*next_q_value td_error=q_estimate - q_value # 计算 MSE 损失 loss = td_error.pow(2).mean() # 根据损失改进网络 optimizer.zero_grad() loss.backward() optimizer.step() if __name__=="__main__": for episode in range(10**5): q_learning() state=((0,), (1,)) state = torch.FloatTensor(state) #.unsqueeze(0) # q 值 qs = model(state) print(qs)
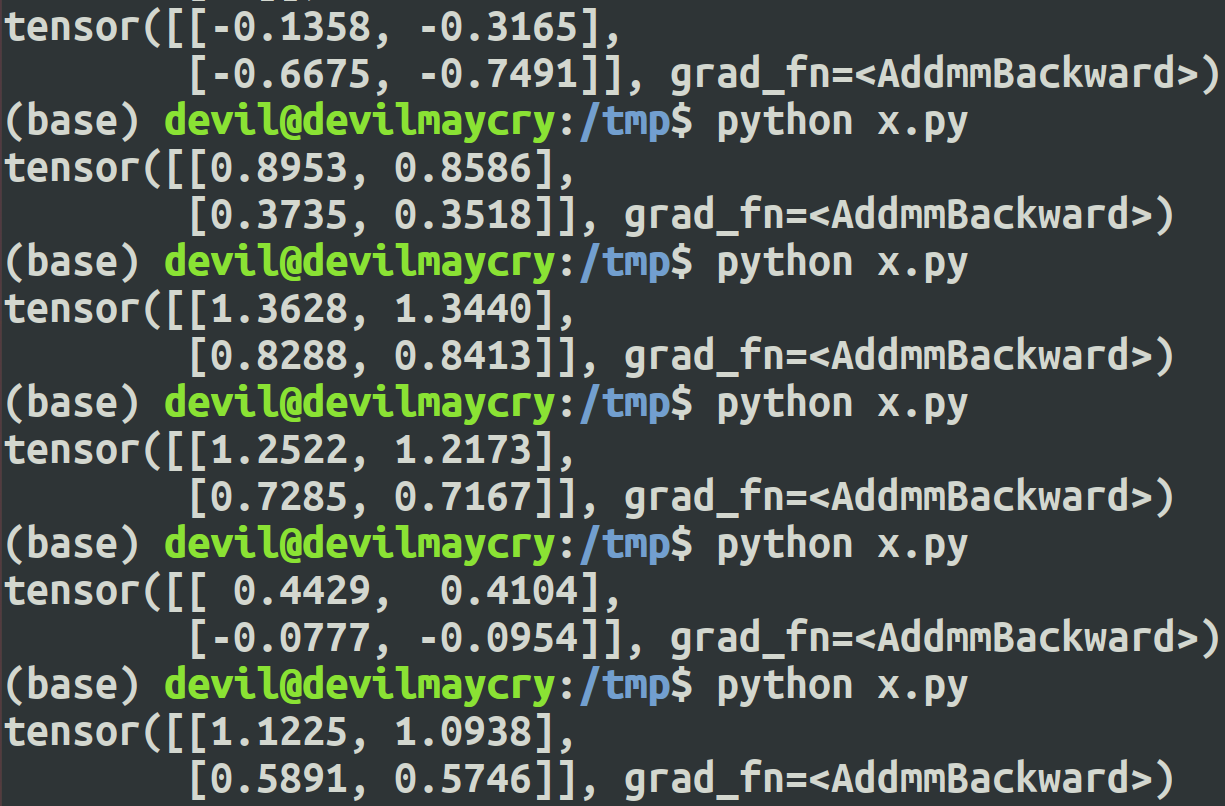
tensor([[1.1225, 1.0938],
[0.5891, 0.5746]], grad_fn=<AddmmBackward>)
得到的结果:
tensor
第一行是状态1的Q值 :
action 1为 1.1225, action 2为1.0938,
第二行是状态2的Q值 :
action 1为 0.5891, action 2为0.5746 。
============================================================
部分素材取自: