SARSA v.s. Q-learning
爬格子问题,是典型的经典强化学习问题。
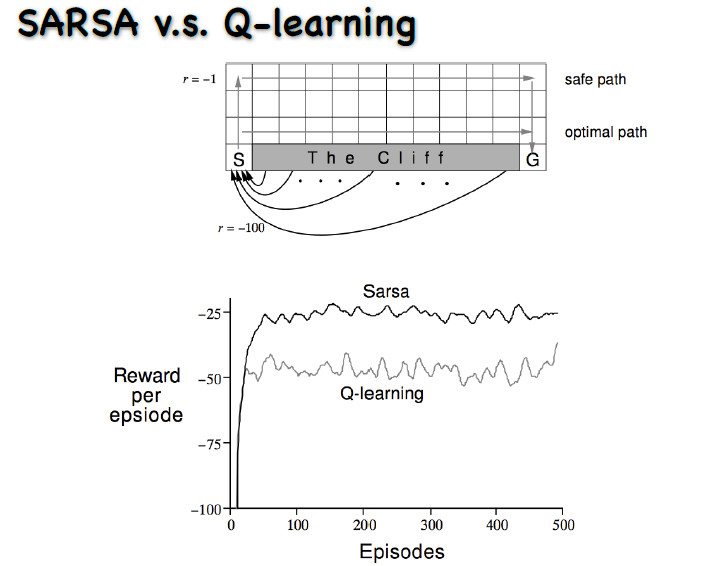
动作是上下左右的走,每走一步就会有一个-1的奖赏。从初始状态走到最终的状态,要走最短的路才能使奖赏最大。图中有一个悬崖,一旦走到悬崖奖赏会极小,而且还要再退回这个初始状态。
个人编写代码如下:
#encoding:UTF-8 #!/usr/bin/env python3 import math import random import matplotlib.pyplot as plt #动作的选择为上,下,左, 右 actions=["up", "down", "left", "right"] #坐标x的范围 x_scope=4 #坐标y的范围 y_scope=12 #greedy策略的探索因子(初始值) epsilon_start=0.4 epsilon_final=0.01 #累积奖赏的折扣因子 discount_factor=0.99 #TD error的学习率 learning_rate=0.1 #动作值的字典 q_value=dict() #回合数 episodes=500 def calc_epsilon(t, epsilon_start=epsilon_start, epsilon_final=epsilon_final, epsilon_decay=episodes): if t<500: epsilon = epsilon_final + (epsilon_start - epsilon_final) * math.exp(-1. * t / epsilon_decay) else: epsilon=0.0 return epsilon #动作值字典初始化 def q_value_init(): q_value.clear() for i in range(x_scope): for j in range(y_scope): #状态坐标 state=(i, j) for action in actions: q_value[(state, action)]=0 #当前状态选择动作后的下一状态及其奖励 def state_reward_transition(state, action): next_x, next_y=state if action=="up": next_x=state[0]-1 elif action=="down": next_x=state[0]+1 elif action=="left": next_y=state[1]-1 else: next_y=state[1]+1 if next_x<0 or next_x>(x_scope-1) or next_y<0 or next_y>(y_scope-1): next_state=state reward=-1 return next_state, reward if next_x==0 and 0<next_y<(y_scope-1): next_state=(0, 0) reward=-100 return next_state, reward next_state=(next_x, next_y) reward=-1 return next_state, reward #最大动作值选择法 def max_action(state): q_value_list=[] for action in actions: q_value_list.append((q_value[(state, action)], action)) random.shuffle(q_value_list) action=max(q_value_list)[-1] return action #greedy策略动作选择法 def greedy_action(state): q_value_list=[] for action in actions: q_value_list.append((q_value[(state, action)], action)) random.shuffle(q_value_list) if random.random()>epsilon: action=max(q_value_list)[-1] else: action=random.choice(q_value_list)[-1] return action #sarsa策略 def sarsa(state): #选择当前状态的动作 action=greedy_action(state) next_state, reward=state_reward_transition(state, action) #选择下一状态的动作 next_action=greedy_action(next_state) #对当前动作值的估计 estimate=reward+discount_factor*q_value[(next_state, next_action)] #TD error error=estimate-q_value[(state, action)] #学习到的新当前动作值 q_value[(state, action)]+=learning_rate*error return next_state, reward def q_learning(state): #选择当前状态的动作 action=greedy_action(state) next_state, reward=state_reward_transition(state, action) #选择下一状态的动作 next_action=max_action(next_state) #对当前动作值的估计 estimate=reward+discount_factor*q_value[(next_state, next_action)] #TD error error=estimate-q_value[(state, action)] #学习到的新当前动作值 q_value[(state, action)]+=learning_rate*error return next_state, reward if __name__=="__main__": reward_list_1=[] q_value_init() for episode in range(episodes+100): reward_sum=0 state=(0, 0) epsilon=calc_epsilon(episode) while state!=(x_scope-1, y_scope-1): state, reward=sarsa(state) reward_sum+=reward reward_list_1.append(reward_sum) for i in range(x_scope): for j in range(y_scope): print("-"*20) for action in actions: print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(211) plt.plot(reward_list_1, label="sarsa") plt.legend(loc = 0) plt.xlabel('episode') plt.ylabel('reward sum per episode') plt.xlim(0,600) plt.ylim(-2000, 0) plt.title("sarsa") reward_list_2=[] q_value_init() for episode in range(episodes+100): reward_sum=0 state=(0, 0) epsilon=calc_epsilon(episode) while state!=(x_scope-1, y_scope-1): state, reward=q_learning(state) reward_sum+=reward reward_list_2.append(reward_sum) for i in range(x_scope): for j in range(y_scope): print("-"*20) for action in actions: print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(212) plt.plot(reward_list_2, label="q-learning") plt.legend(loc = 0) plt.xlabel('episode') plt.ylabel('reward sum per episode') plt.xlim(0,600) plt.ylim(-2000, 0) plt.title("q-learning") plt.show() plt.plot(reward_list_1, label="sarsa") plt.plot(reward_list_2, label="q-learning") plt.legend(loc = 0) plt.xlabel('episode') plt.ylabel('reward sum per episode') plt.xlim(0,600) plt.ylim(-2000, 0) plt.title("SARSA & Q-LEARNING") plt.show()

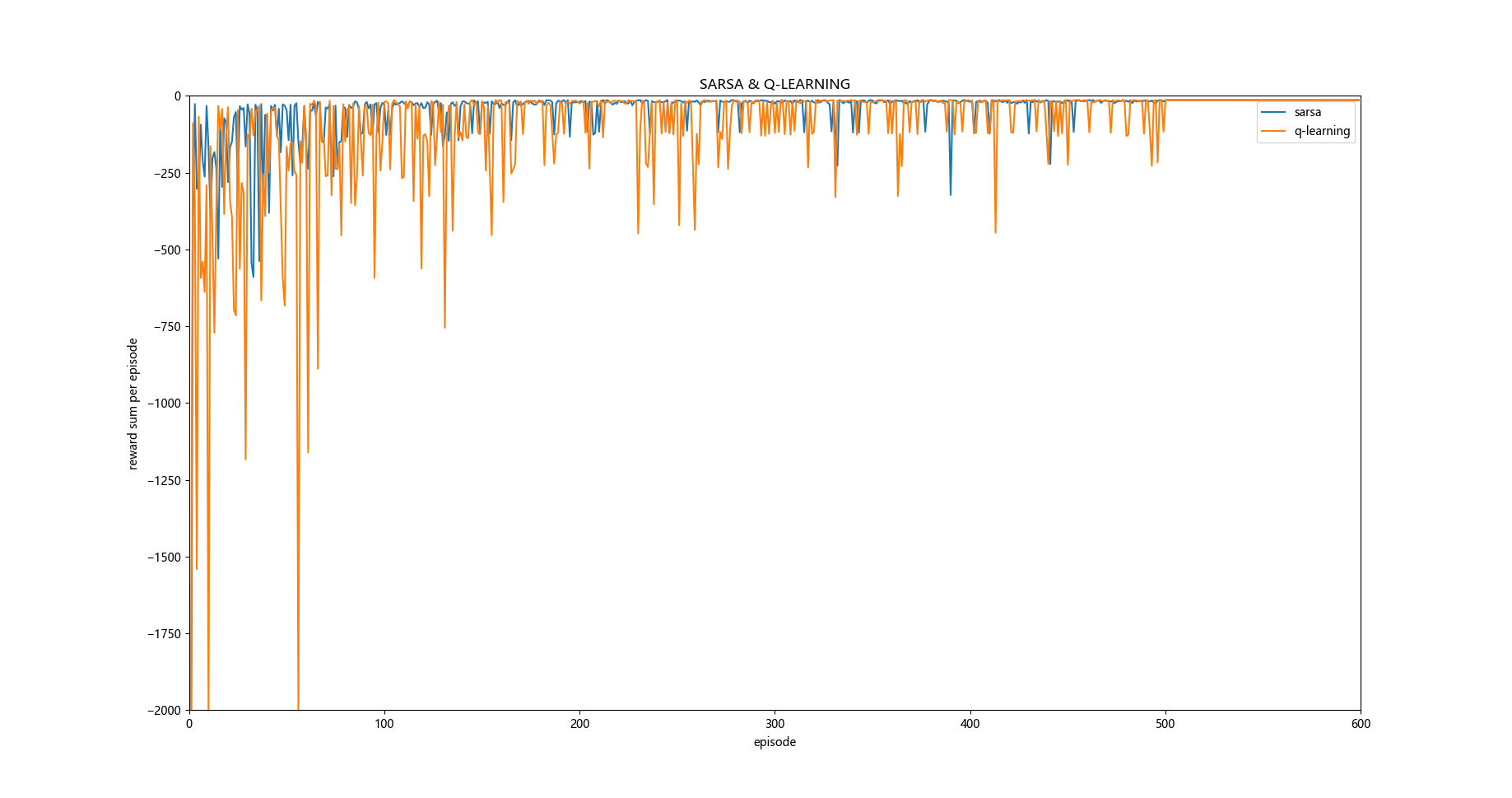
从自我编写的代码运行的程序效果和原题目给出的效果图来看还是有些差距的,个人感觉这个应该是超参数设置的问题。
如:学习率, greedy策略的epsilon设置等。
不过有一点是相似的,那就是q-learning学习的过程中奖励值一般要小于sarsa学习方法。
对于为什么在这个问题中 q-learning的学习过程中奖励值的累积和要普遍小于sarsa方法,个人观点是按照原题目给出的效果图分析是因为sarsa对策略的探索更加高效, 更有可能走optimal path, 而q-learning 对下一状态q值的探索是直接用最大值来估计的,所以更有可能走safe path路线。
=================================================================
如果这个问题中没有悬崖的话,那么运行结果如何呢?
代码如下:
#encoding:UTF-8 #!/usr/bin/env python3 import math import random import matplotlib.pyplot as plt #动作的选择为上,下,左, 右 actions=["up", "down", "left", "right"] #坐标x的范围 x_scope=4 #坐标y的范围 y_scope=12 #greedy策略的探索因子(初始值) epsilon_start=0.4 epsilon_final=0.01 #累积奖赏的折扣因子 discount_factor=0.99 #TD error的学习率 learning_rate=0.1 #动作值的字典 q_value=dict() #回合数 episodes=500 def calc_epsilon(t, epsilon_start=epsilon_start, epsilon_final=epsilon_final, epsilon_decay=episodes): if t<500: epsilon = epsilon_final + (epsilon_start - epsilon_final) * math.exp(-1. * t / epsilon_decay) else: epsilon=0.0 return epsilon #动作值字典初始化 def q_value_init(): q_value.clear() for i in range(x_scope): for j in range(y_scope): #状态坐标 state=(i, j) for action in actions: q_value[(state, action)]=0 #当前状态选择动作后的下一状态及其奖励 def state_reward_transition(state, action): next_x, next_y=state if action=="up": next_x=state[0]-1 elif action=="down": next_x=state[0]+1 elif action=="left": next_y=state[1]-1 else: next_y=state[1]+1 if next_x<0 or next_x>(x_scope-1) or next_y<0 or next_y>(y_scope-1): next_state=state reward=-1 return next_state, reward """ if next_x==0 and 0<next_y<(y_scope-1): next_state=(0, 0) reward=-100 return next_state, reward """ next_state=(next_x, next_y) reward=-1 return next_state, reward #最大动作值选择法 def max_action(state): q_value_list=[] for action in actions: q_value_list.append((q_value[(state, action)], action)) random.shuffle(q_value_list) action=max(q_value_list)[-1] return action #greedy策略动作选择法 def greedy_action(state): q_value_list=[] for action in actions: q_value_list.append((q_value[(state, action)], action)) random.shuffle(q_value_list) if random.random()>epsilon: action=max(q_value_list)[-1] else: action=random.choice(q_value_list)[-1] return action #sarsa策略 def sarsa(state): #选择当前状态的动作 action=greedy_action(state) next_state, reward=state_reward_transition(state, action) #选择下一状态的动作 next_action=greedy_action(next_state) #对当前动作值的估计 estimate=reward+discount_factor*q_value[(next_state, next_action)] #TD error error=estimate-q_value[(state, action)] #学习到的新当前动作值 q_value[(state, action)]+=learning_rate*error return next_state, reward def q_learning(state): #选择当前状态的动作 action=greedy_action(state) next_state, reward=state_reward_transition(state, action) #选择下一状态的动作 next_action=max_action(next_state) #对当前动作值的估计 estimate=reward+discount_factor*q_value[(next_state, next_action)] #TD error error=estimate-q_value[(state, action)] #学习到的新当前动作值 q_value[(state, action)]+=learning_rate*error return next_state, reward if __name__=="__main__": reward_list_1=[] q_value_init() for episode in range(episodes+100): reward_sum=0 state=(0, 0) epsilon=calc_epsilon(episode) while state!=(x_scope-1, y_scope-1): state, reward=sarsa(state) reward_sum+=reward reward_list_1.append(reward_sum) for i in range(x_scope): for j in range(y_scope): print("-"*20) for action in actions: print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(211) plt.plot(reward_list_1, label="sarsa") plt.legend(loc = 0) plt.xlabel('episode') plt.ylabel('reward sum per episode') plt.xlim(0,600) plt.ylim(-2000, 0) plt.title("sarsa") reward_list_2=[] q_value_init() for episode in range(episodes+100): reward_sum=0 state=(0, 0) epsilon=calc_epsilon(episode) while state!=(x_scope-1, y_scope-1): state, reward=q_learning(state) reward_sum+=reward reward_list_2.append(reward_sum) for i in range(x_scope): for j in range(y_scope): print("-"*20) for action in actions: print( "("+str(i)+", "+str(j)+") : "+action+" "+str(q_value[((i, j), action)])) plt.subplot(212) plt.plot(reward_list_2, label="q-learning") plt.legend(loc = 0) plt.xlabel('episode') plt.ylabel('reward sum per episode') plt.xlim(0,600) plt.ylim(-2000, 0) plt.title("q-learning") plt.show() plt.plot(reward_list_1, label="sarsa") plt.plot(reward_list_2, label="q-learning") plt.legend(loc = 0) plt.xlabel('episode') plt.ylabel('reward sum per episode') plt.xlim(0,600) plt.ylim(-2000, 0) plt.title("SARSA & Q-LEARNING") plt.show()
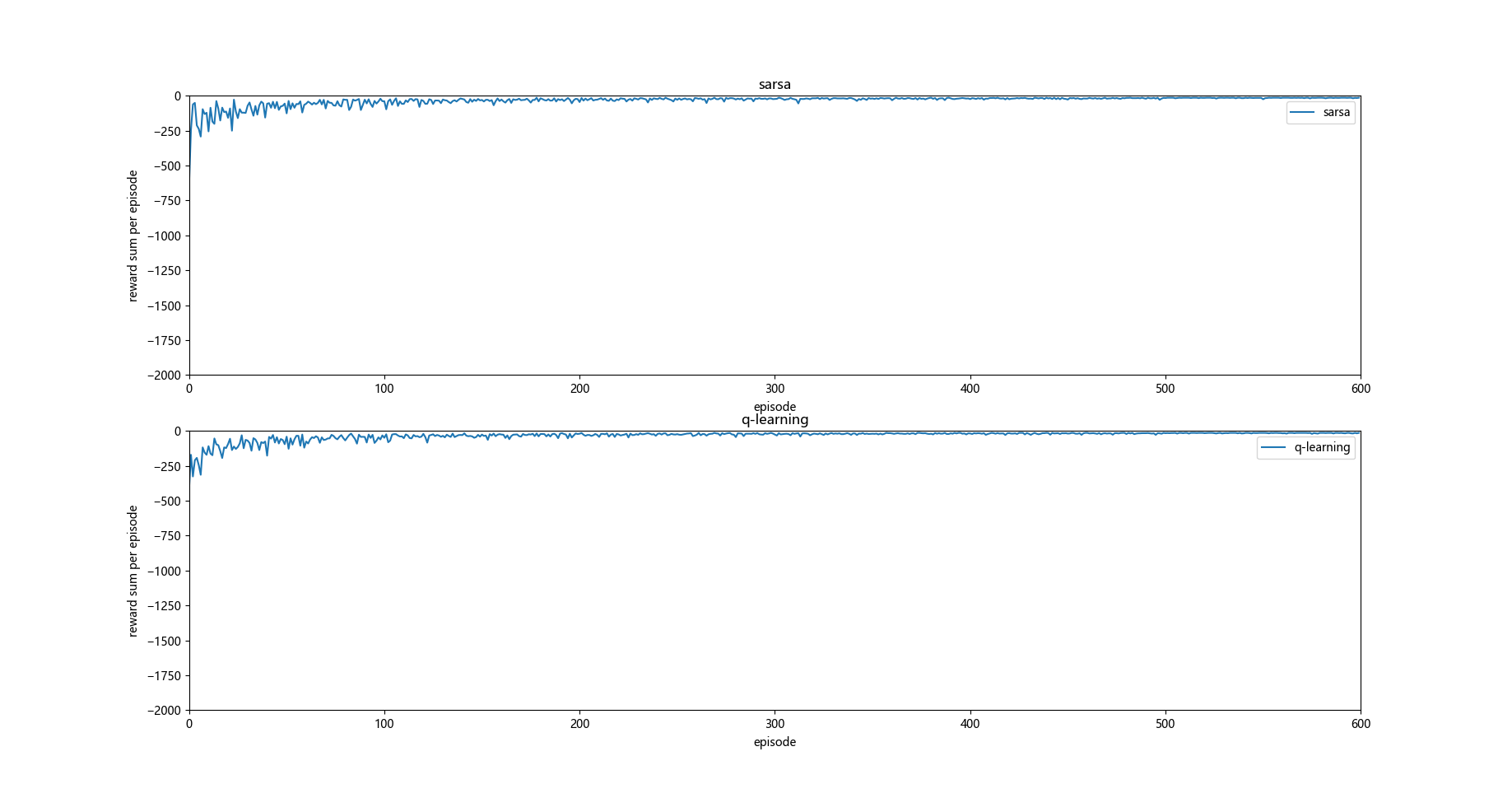

这时候发现如果没有悬崖的话 q-learning 和 sarsa 运行的效果大致相同。
个人观点:
如果按照原题目给出的效果图分析 q_learning 学习对惩罚项敏感,探索效率低于sarsa, 因为q_learning中对下一状态的q值采用max方法来估计,所以在算法运行过程中会尽量远离初步判断不好的选择,即选择safe path, 某种角度上来说也是其探索效率小于sarsa的一个结果。

按照原题目效果图分析并结合上图所示, S0状态是初始状态,在q_learning 算法初始时容易得出S1状态时right动作的q值较低的结论,原因是S2状态时up操作的q值较低,S3状态时q值较高,所以q_learning更倾向于在S1状态选择down操作。
但是依照个人所做实验的效果图分析,则和上面的分析不太一样:
那就是 q_learning更偏向于探索optimal path, 而sarsa更倾向于探索safe path, 因为正是因为q_learning 探索optimal path才会有多次掉入悬崖的情况,而sarsa掉入悬崖次数较少则说明其更倾向于探索safe path 。