二叉搜索树:一棵二叉搜索树是以一棵二叉树来组织的,这样一棵树可以使用链表的数据结构来表示(也可以采用数组来实现)。除了key和可能带有的其他数据外,每个节点还包含Left,Right,Parent,它们分别指节点的左孩子,右孩子,和父节点。
一个二叉搜索树总是满足 :node.left.key<node.key<=node.right.key。
以下是一个用java实现的二叉搜索树,包含了查找最大值,最小值,查找某一节点,插入和删除操作。
接下来通过代码来分析二叉搜索树中的思想:在代码实现二叉搜索树中,大量采用了递归的思想,同样可以采用循环去递归来实现。
插入:自根节点起递归调用“寻找合适位置方法”,使二叉搜索树始终满足条件 node.left.key<node.key<=node.right.key。
查询:自根节点起递归调用“查找孩子的方法”。查找孩子的方法采用的思想是,判断node.key==key 返回,node.key>key 递归查找左子树,node.key<=key 递归查 找右子树。
查询最小值:递归查找左孩子,直到最后一个左孩子。
查询最大值:递归查找右孩子,直到最后一个右孩子。
遍历:
前序遍历:根的关键字输出在左右子树的关键字之前。根 左 右。
中序遍历:根的关键字输出在左右子树的关键字之间。左 根 右。
后序遍历:根的关键字输出在左右子树的关键字之后。左 右 根。
删除:删除一棵搜索树是比较麻烦的。共有以下4种情况
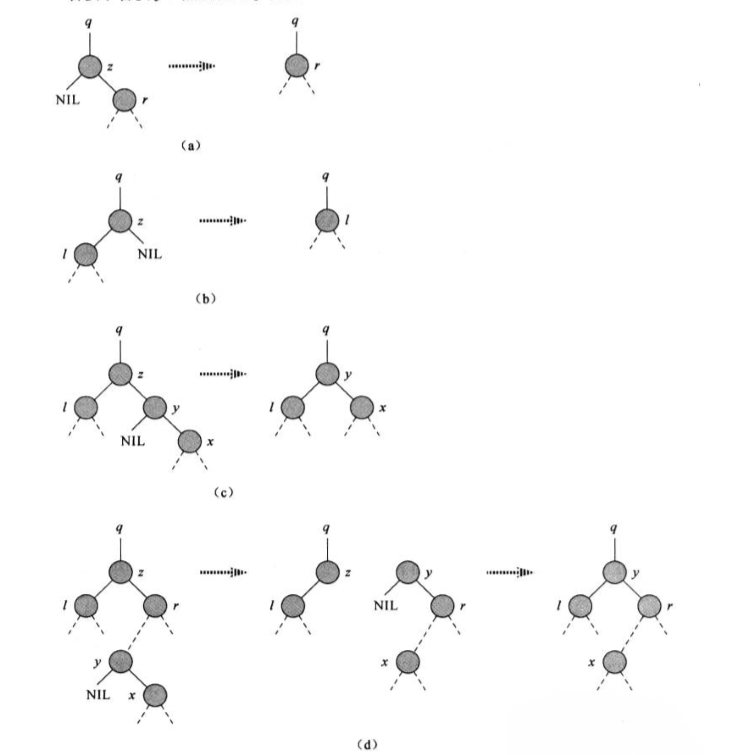
1.删除节点没有孩子,直接断开连接即可
2.a图:删除节点没有左孩子,将右孩子移至删除节点处
3.b图:删除节点没有右孩子,将左孩子移至删除节点处
4.c图:有左右孩子,右孩子 没有 左孩子,将右孩子移动至删除节点处,将左孩子的父节点连接值右孩子。
5.d图:有左右孩子,且右孩子也有左右孩子,则查找右孩子的最小节点,将最小节点移至删除节点处。
public class SearchTree {
//树的根节点
private Node Root = null;
//内部类,结点
private class Node{
Node parent;//父节点
Node Left;//左孩子
Node Right;//右孩子
int keyValue;//关键字
public Node(Node parent,
Node Left,
Node Right,
int keyValue) {
this.parent = parent;
this.Left = Left;
this.Right = Right;
this.keyValue = keyValue;
}
}
public void delete(int value) {
Node deleteNode = this.search(value);//查找删除节点
if(deleteNode.Left==null) {//没有左孩子
transplant(deleteNode, deleteNode.Right);
}else if(deleteNode.Right==null) {//没有右孩子
transplant(deleteNode, deleteNode.Left);
}else {//有左右孩子时
Node min = this.min(deleteNode.Right);//查找右孩子的最小节点
if(min.parent!=deleteNode) {
transplant(min, min.Right);
min.Right = deleteNode.Right;
min.Right.parent = min;
}
transplant(deleteNode, min);
min.Left = deleteNode.Left;
min.Left.parent = min;
}
}
//交换子树,将node2 移动至node1的位置。
private void transplant(Node node1,Node node2) {
if(node1.parent==null) {
this.Root = node2;
}else if(node1==node1.parent.Left) {
node1.parent.Left = node2;
}else {
node1.parent.Right= node2;
}
if(node2!=null) {
node2.parent = node1.parent;
}
}
//查找方法
public Node search(int value) {
return searchNode(this.Root,value);
}
private Node searchNode(Node node,int key) {
if(node==null || node.keyValue==key) {
return node;
}
if(node.keyValue>key) {
return this.searchNode(node.Left,key);
}else {
return this.searchNode(node.Right, key);
}
}
//插入方法
public void insert(int value) {
Node child = new Node(null, null, null, value);
findRightPlace(this.Root,child);
}
private void findRightPlace(Node currentRoot,Node insertNode) {
if(currentRoot!=null) {
if(currentRoot.keyValue>insertNode.keyValue) {
if(currentRoot.Left==null) {
currentRoot.Left = insertNode;
insertNode.parent = currentRoot;
}else {
findRightPlace(currentRoot.Left,insertNode);
}
}else {
if(currentRoot.Right==null) {
currentRoot.Right = insertNode;
insertNode.parent = currentRoot;
}else {
findRightPlace(currentRoot.Right,insertNode);
}
}
}else {
this.Root = insertNode;
}
}
//查找最大
public int findMax() {
return max(this.Root)==null?-1:max(this.Root).keyValue;
}
private Node max(Node node) {
if(node!=null) {
if(node.Right!=null) {
return max(node.Right);
}else {
return node;
}
}else {
return null;
}
}
//查找最小
public int findMin() {
return min(this.Root)==null?-1:min(this.Root).keyValue;
}
private Node min(Node node) {
if(node!=null) {
if(node.Left!=null) {
return min(node.Left);
}else {
return node;
}
}else {
return null;
}
}
//后序遍历
public void after() {
afterShow(this.Root);
}
private void afterShow(Node node) {
if(node!=null) {
afterShow(node.Left);
afterShow(node.Right);
System.out.println(node.keyValue);
}
}
//中序遍历
public void mid() {
midShow(this.Root);
}
private void midShow(Node node) {
if(node!=null) {
midShow(node.Left);
System.out.println(node.keyValue);
midShow(node.Right);
}
}
//前序遍历
public void ahead() {
aheadShow(this.Root);
}
private void aheadShow(Node node) {
if(node!=null) {
System.out.println(node.keyValue);
aheadShow(node.Left);
aheadShow(node.Right);
}
}
参考资料 《算法导论》第三版