参考书籍:《机器学习》(周志华)
说 明:本篇内容为读书笔记,主要参考教材为《机器学习》(周志华)。详细内容请参阅书籍——第4章 决策树。部分内容参考网络资源,在此感谢所有原创者的工作。
=================================================================
第一部分 理论基础
1. 纯度(purity)
对于一个分支结点,如果该结点所包含的样本都属于同一类,那么它的纯度为1,而我们总是希望纯度越高越好,也就是尽可能多的样本属于同一类别。那么如何衡量“纯度”呢?由此引入“信息熵”的概念。
2. 信息熵(information entropy)
假定当前样本集合D中第k类样本所占的比例为pk(k=1,,2,...,|y|),则D的信息熵定义为:
Ent(D) = -∑k=1 pk·log2 pk (约定若p=0,则log2 p=0)
显然,Ent(D)值越小,D的纯度越高。因为0<=pk<= 1,故log2 pk<=0,Ent(D)>=0. 极限情况下,考虑D中样本同属于同一类,则此时的Ent(D)值为0(取到最小值)。当D中样本都分别属于不同类别时,Ent(D)取到最大值log2 |y|.
3. 信息增益(information gain)
假定离散属性a有V个可能的取值{a1,a2,...,aV}. 若使用a对样本集D进行分类,则会产生V个分支结点,记Dv为第v个分支结点包含的D中所有在属性a上取值为av的样本。不同分支结点样本数不同,我们给予分支结点不同的权重:|Dv|/|D|, 该权重赋予样本数较多的分支结点更大的影响、由此,用属性a对样本集D进行划分所获得的信息增益定义为:
Gain(D,a) = Ent(D)-∑v=1 |Dv|/|D|·Ent(Dv)
其中,Ent(D)是数据集D划分前的信息熵,∑v=1 |Dv|/|D|·Ent(Dv)可以表示为划分后的信息熵。“前-后”的结果表明了本次划分所获得的信息熵减少量,也就是纯度的提升度。显然,Gain(D,a) 越大,获得的纯度提升越大,此次划分的效果越好。
4. 增益率(gain ratio)
基于信息增益的最优属性划分原则——信息增益准则,对可取值数据较多的属性有所偏好。C4.5算法使用增益率替代信息增益来选择最优划分属性,增益率定义为:
Gain_ratio(D,a) = Gain(D,a)/IV(a)
其中
IV(a) = -∑v=1 |Dv|/|D|·log2 |Dv|/|D|
称为属性a的固有值。属性a的可能取值数目越多(即V越大),则IV(a)的值通常会越大。这在一定程度上消除了对可取值数据较多的属性的偏好。
事实上,增益率准则对可取值数目较少的属性有所偏好,C4.5算法并不是直接使用增益率准则,而是先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
5. 基尼指数(Gini index)
CART决策树算法使用基尼指数来选择划分属性,基尼指数定义为:
Gini(D) = ∑k=1 ∑k'≠1 pk·pk' = 1- ∑k=1 pk·pk
可以这样理解基尼指数:从数据集D中随机抽取两个样本,其类别标记不一致的概率。Gini(D)越小,纯度越高。
属性a的基尼指数定义:
Gain_index(D,a) = ∑v=1 |Dv|/|D|·Gini(Dv)
使用基尼指数选择最优划分属性,即选择使得划分后基尼指数最小的属性作为最优划分属性。
第二部分 编码实现——基于信息增益准则的决策树
采用Python作为实现工具,以书籍中的西瓜数据为例,构造一棵“watermelon tree”。这里,我们构建的是一棵基于信息增益准则的决策树,比较简单,适合初学。
1. 算法
此处先略。^_^
2. Python代码实现
代码框架参考了部分网络资源,然后就是闷头去写了。本质上都是大同小异,重要的还是抱着学习的心态,去自主实现一下,才能对决策树有更多的思考。
2.1 数据样本说明
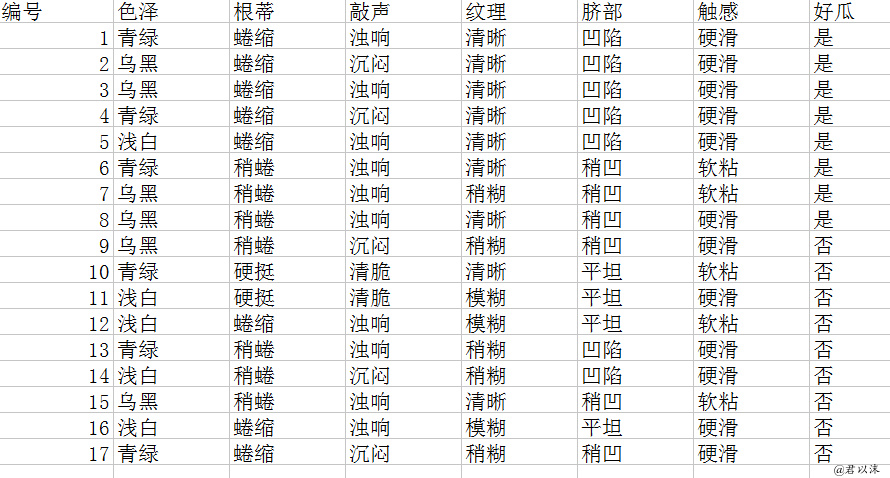
本案例基于教材《机器学习》P76表4.1 西瓜数据集2.0,尝试用Python实现决策树构建。一共17条样本数据。理论上,建立的树应该和P78图4.4一致。
样本数据截图如下:
2.2 实现代码
(一)导入模块部分
#导入模块 import pandas as pd import numpy as np from collections import Counter from math import log2
用pandas模块的read_excel()函数读取数据文本;用numpy模块将dataframe转换为list(列表);用Counter来完成计数;用math模块的log2函数计算对数。后边代码中会有对应体现。
(二)数据获取与处理函数
#数据获取与处理 def getData(filePath): data = pd.read_excel(filePath) return data def dataDeal(data): dataList = np.array(data).tolist() dataSet = [element[1:] for element in dataList] return dataSet
getData()通过pandas模块中的read_excel()函数读取样本数据。尝试过将数据文件保存为csv格式,但是对于中文的处理不是很好,所以选择了使用xls格式文件。
dataDeal()函数将dataframe转换为list,并且去掉了编号列。编号列并不是西瓜的属性,事实上,如果把它当做属性,会获得最大的信息增益。
这两个函数是完全可以合并为同一个函数的,但是因为我想分别使用data(dataframe结构,带属性标签)和dataSet(list)数据样本,所以分开写了两个函数。
(三)获取属性名称
#获取属性名称 def getLabels(data): labels = list(data.columns)[1:-1] return labels
很简单,获取属性名称:纹理,色泽,根蒂,敲声,脐部,触感。
(四)获取类别标记
#获取类别标记 def targetClass(dataSet): classification = set([element[-1] for element in dataSet]) return classification
获取一个样本是否好瓜的标记(是与否)。
(五)叶结点标记
#将分支结点标记为叶结点,选择样本数最多的类作为类标记 def majorityRule(dataSet): mostKind = Counter([element[-1] for element in dataSet]).most_common(1) majorityKind = mostKind[0][0] return majorityKind
(六)计算信息熵
#计算信息熵 def infoEntropy(dataSet): classColumnCnt = Counter([element[-1] for element in dataSet]) Ent = 0 for symbol in classColumnCnt: p_k = classColumnCnt[symbol]/len(dataSet) Ent = Ent-p_k*log2(p_k) return Ent
(七)子数据集构建
#子数据集构建 def makeAttributeData(dataSet,value,iColumn): attributeData = [] for element in dataSet: if element[iColumn]==value: row = element[:iColumn] row.extend(element[iColumn+1:]) attributeData.append(row) return attributeData
在某一个属性值下的数据,比如纹理为清晰的数据集。
(八)计算信息增益
#计算信息增益 def infoGain(dataSet,iColumn): Ent = infoEntropy(dataSet) tempGain = 0.0 attribute = set([element[iColumn] for element in dataSet]) for value in attribute: attributeData = makeAttributeData(dataSet,value,iColumn) tempGain = tempGain+len(attributeData)/len(dataSet)*infoEntropy(attributeData) Gain = Ent-tempGain return Gain
(九)选择最优属性
#选择最优属性 def selectOptimalAttribute(dataSet,labels): bestGain = 0 sequence = 0 for iColumn in range(0,len(labels)):#不计最后的类别列 Gain = infoGain(dataSet,iColumn) if Gain>bestGain: bestGain = Gain sequence = iColumn print(labels[iColumn],Gain) return sequence
(十)建立决策树
#建立决策树 def createTree(dataSet,labels): classification = targetClass(dataSet) #获取类别种类(集合去重) if len(classification) == 1: return list(classification)[0] if len(labels) == 1: return majorityRule(dataSet)#返回样本种类较多的类别 sequence = selectOptimalAttribute(dataSet,labels) print(labels) optimalAttribute = labels[sequence] del(labels[sequence]) myTree = {optimalAttribute:{}} attribute = set([element[sequence] for element in dataSet]) for value in attribute: print(myTree) print(value) subLabels = labels[:] myTree[optimalAttribute][value] = createTree(makeAttributeData(dataSet,value,sequence),subLabels) return myTree
树本身并不复杂,采用递归的方式实现。
(十一)定义主函数
def main(): filePath = 'watermelonData.xls' data = getData(filePath) dataSet = dataDeal(data) labels = getLabels(data) myTree = createTree(dataSet,labels) return myTree
主函数随便写写了,主要是实现功能。
(十二)生成树
if __name__ == '__main__': myTree = main()
3.几点说明
Python实现并没有很复杂的东西,只要能很好的理解递归在这里是如何体现的就足够了。
在构造树的时候,这里的树定义为一个嵌套的字典(dict)结构,树根对应的属性是字典最外层的关键字,其值是仍一个字典。递归就是这样用下一层返回的树作为上一层树某个分支(字典的关键字)的值,一层层往下(一棵倒树)填充,直至遇到叶结点。在定义的构造树函数中,终止条件(两个if)是很重要的,决定了递归在什么时候停止,也就是树在什么时候停止生长。
生成的树(字典结构)如下:

一个字典结构的树是极其不友好的,暂时没有将其可视化,后续会学习一下。
从结果看,根节点的属性是纹理。纹理为稍糊的,下一个结点的属性是触感,触感为软粘的瓜,判断为好瓜(纹理为稍糊且触感为软粘的瓜),触感为硬滑的瓜,判定为坏瓜(纹理为稍糊且触感为硬滑的瓜)。纹理为模糊的,直接判定为坏瓜(买瓜的要注意了);纹理为清晰的情形较为复杂。纹理为清晰的,下一个结点属性为根蒂,对于根蒂为硬挺的,判断为坏瓜(纹理为清晰且根蒂为硬挺的瓜),根蒂为蜷缩的,判断为好瓜(纹理为清晰且根蒂为蜷缩的瓜)。根蒂为稍蜷的,下一个结点的属性是色泽,对于色泽为青绿的,判断为好瓜(纹理为清晰,根蒂为稍蜷且色泽为青绿的瓜),对于色泽为乌黑的,下一个结点属性是触感,对于触感为软粘的,判定为坏瓜(纹理为清晰,根蒂为稍蜷,色泽为乌黑且触感为软粘的瓜),对于触感为硬滑的,判定为好瓜(纹理为清晰,根蒂为稍蜷,色泽为乌黑且触感为硬滑的瓜)。这里有一个小的问题,一会儿再说。
先看《机器学习》教材上给出的树:
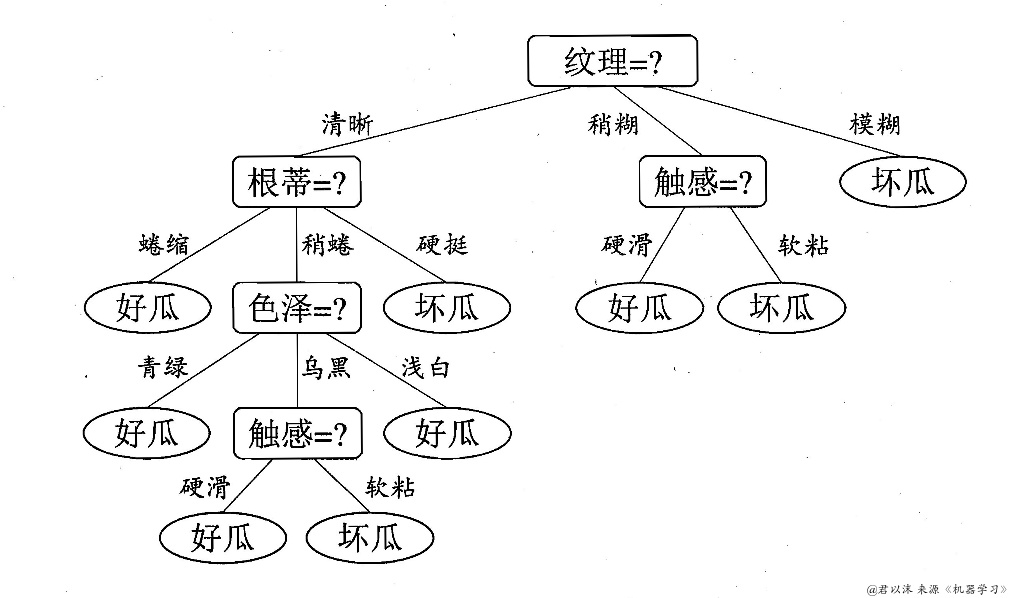
我们获得的结果和书本中的结果基本是一致的,唯一的一个区别是我们缺少一个叶——色泽为浅白的叶。这是因为,样本数据中不存在纹理为清晰、根蒂为稍蜷且色泽为浅白的瓜,导致在生成树的时候少了一个叶。这种情况需要特殊处理,比如处理成父类的类别。这里没有多做处理,该机制添加进去并不难。
4.写在最后
热烈庆祝在帝都正式工作的第100天!(✿✿ヽ(°▽°)ノ✿)

(晚上加个班的好处就是可以看看书,做点自己喜欢的事——回家吃饭(#^.^#))