浅谈平衡树splay

• 首先splay和treap不一样，treap通过随机数来调整树的形态。但splay不一样，再每插入或操作一次后，你都会把他旋转到根，再旋转过程中树的形态会不断改变，这样来达到均摊效果 常数据大。

• 来看看具体实现吧
  首先定义数组，(size) 子树大小（包括自己），(fa) 节点的父亲，(key) 该节点的权值，(cnt) 该节点权值出现次数，$ch $表示儿子 0表左二子，1表右儿子

首先看几个简单函数

inline void update(int x)
{
	size[x]=cnt[x]+size[ch[x][0]]+size[ch[x][1]];
}

更新子树大小

inline int get(int x){return x==ch[fa[x]][1];}

返回该节点是left儿子还是right儿子

inline void clear(int x){ch[x][0]=ch[x][1]=fa[x]=size[x]=cnt[x]=key[x]=0;}

删除该节点，清空所有信息

接下来是splay的精髓所在

inline void rotate(int x,int &k)
{
    static int old,oldfa,o;
    old=fa[x];oldfa=fa[old];o=get(x);
    if(old==k)k=x;
    else ch[oldfa][get(old)]=x;
    fa[x]=oldfa;
    ch[old][o]=ch[x][o^1];fa[ch[x][o^1]]=old;
    ch[x][o^1]=old;fa[old]=x;
    update(x),update(old);
}
inline void splay(int x,int &k)
{
    while(x!=k)
    {
        if(fa[x]!=k)rotate(get(x)^get(fa[x])?x:fa[x],k);
        rotate(x,k);
    }
}

rotate，splay，是splay核心操作，显然splay是依赖于rotate的，让我们看一下rotate是如何实现的吧

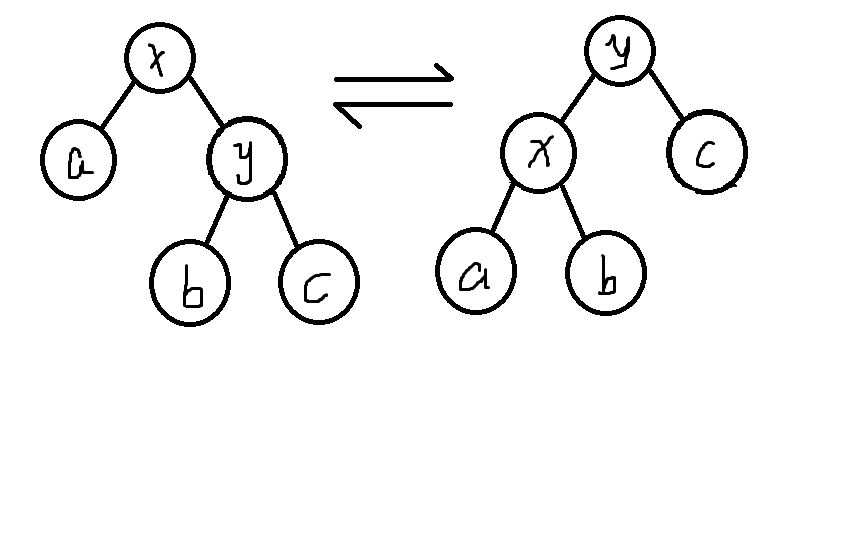
（手绘图）
我们考虑从图上左往右的过程，我们要将y旋上去，因为y本是x的右儿子，所以x放到y的左儿子，将y的原本左儿子设为x的右儿子，这是左旋，还有对称操作右旋，但我们不必要打两个函数，用 ^可以实现左右儿子的转换，用get操作实现，具体实现参考代码，打代码时最好画个图参照一下。

splay，这个操作完全依靠rotate，目的就是把你要的节点旋转到k（一般是root），k要传地址，要修改。在while循环里加了个小小的优化，但x和他的fa在同一侧时可以旋fa，以此来改变树的形态，(不怕被卡可以不写)

inline void insert(int x)
{
    if(!root){root=++sz;size[sz]=cnt[sz]=1;key[sz]=x;return;}
    int now=root,o;
    while(1)
    {
        if(x==key[now])
        {
            ++cnt[now];
            splay(now,root);
            update(now);
			return;
        }
        o=x>key[now]?1:0;
        if(!ch[now][o])
        {
            ch[now][o]=++sz;
            size[sz]=cnt[sz]=1;
            key[sz]=x;fa[sz]=now;
            splay(sz,root);
            return;
        }
        else now=ch[now][o];
    }
}

insert，插入一个数，当没有数时就直接把这个数设为根，else 因为树满足二叉排序树的性质，所以比当前节点的key小就往左走，否则往右走，直到找到一个空节点，更新信息，由于这个点以上所有的点(size)都要加一，不好update，所以把这给点旋转到根，将这个点update就行了

inline int find_pos(int x)
{
    int now=root;
    while(1)
    {
        if(x==key[now]){return now;}
        if(x<key[now])now=ch[now][0];
        else now=ch[now][1];
    }
}

找到该值在树中的节点编号

inline int pre()
{
        int now=ch[root][0];
	while(ch[now][1])now=ch[now][1];
	return now;
}
inline int nex()
{
        int now=ch[root][1];
	while(ch[now][0])now=ch[now][0];
	return now;
}

求前驱，后继，前驱从根的左儿子开始一直往右跑，后继从根的右儿子开始一直往左跑即可

void del(int x)
{
    splay(find_pos(x),root);
    if(cnt[root]>1){--cnt[root];return;}
    if(!ch[root][0]&&!ch[root][1]){clear(root);root=0;return;}
    if(ch[root][0]&&ch[root][1])
    {
        int oldroot=root;
        splay(pre(),root);
        fa[ch[oldroot][1]]=root;
        ch[root][1]=ch[oldroot][1];
        clear(oldroot);
        update(root);
    }
    else
    {
        int o=ch[root][1]>0;
        root=ch[root][o];
        clear(fa[root]);
        fa[root]=0;
    }
}

删除操作，有点麻烦，先找到x的位置

• 如果x有多个就(cnt)减一
• 如果一个儿子都没有就直接删掉，root设为0
• 如果 只有一个儿子就把儿子设为根，删去这个点
• 剩下两个儿子情况，找到根的前驱，把前驱旋到根，这是root只有左儿子，再把原来根的右儿子到root上，这样原来的root就脱离了树，再删掉即可。

inline int find_order_of_key(int x)
{
    int res=0,now=root;
    while(1)
    {
        if(x<key[now])now=ch[now][0];
        else
        {
            res+=size[ch[now][0]];
            if(x==key[now]){splay(now,root);return res+1;}
            res+=cnt[now];
            now=ch[now][1];
        }
    }
}
inline int find_by_order(int x)
{
    int now=root;
    while(1)
    {
        if(x<=size[ch[now][0]])now=ch[now][0];
        else
        {
            int temp=size[ch[now][0]]+cnt[now];
            if(x<=temp)return key[now];
            else{x-=temp;now=ch[now][1];}
        }
    }
}

找x的排名，与找排名为x的数，其实大同小异，用二叉搜索树的性质即可，只是记得答案不一样罢了

inline void rever(int x)
{
    swap(ch[x][0],ch[x][1]);
    rev[ch[x][0]]^=1;rev[ch[x][1]]^=1;
    rev[x]=0;
}
inline void rever(int l,int r)
{
	l=find(l-1);r=find(r+1);
        splay(l,root);splay(r,ch[l][1]);
        rev[ch[r][0]]^=1;
}

找到区间左边一个和区间的右边一个点在树中位置，把左边的点旋转到根，再把右边的点旋到root的右儿子，这时这段区间一定是ch[r][0]的子树（想一想，为什么）（根据二叉搜索树的性质），把这个点打上标记即可；当遇到有翻转标记的点时，交换其左右子树，并下传标记即可，注意，翻转操作只有可能在维护无序数列时使用，在有序数列中不需要也不能翻转，不然就无法满足排序二叉树的性质。
翻转操作在找节点的编号时才执行，详见下面代码

ok，splay的基本操作就是这些了

下面是完整代码
洛谷P3369 treap模板
题目描述
您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

插入x数

删除x数(若有多个相同的数，因只删除一个)

查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，因输出最小的排名)

查询排名为x的数

求x的前驱(前驱定义为小于x，且最大的数)
求x的后继(后继定义为大于x，且最小的数)

#include<bits/stdc++.h>
using namespace std;
typedef int sign;
typedef long long ll;
#define For(i,a,b) for(register sign i=(sign)a;i<=(sign)b;++i)
#define Fordown(i,a,b) for(register sign i=(sign)a;i>=(sign)b;--i)
const int N=1e5+5;
void cmax(sign &a,sign b){if(a<b)a=b;}
void cmin(sign &a,sign b){if(a>b)a=b;}
template<typename T>T read()
{
    T ans=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)&&ch!='-')ch=getchar();
    if(ch=='-')f=-1,ch=getchar();
    while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch-'0'),ch=getchar();
    return ans*f;
}
void file()
{
    #ifndef ONLINE_JUDGE
        freopen("splay.in","r",stdin);
        freopen("splay.out","w",stdout);
    #endif
}
int fa[N],size[N],key[N],cnt[N],ch[N][2],sz,root;
inline void update(int x){size[x]=cnt[x]+size[ch[x][0]]+size[ch[x][1]];}
inline int get(int x){return x==ch[fa[x]][1];}
inline void clear(int x){ch[x][0]=ch[x][1]=fa[x]=size[x]=cnt[x]=key[x]=0;}
inline void rotate(int x,int &k)
{
    static int old,oldfa,o;
    old=fa[x];oldfa=fa[old];o=get(x);
    if(old==k)k=x;
    else ch[oldfa][get(old)]=x;
    fa[x]=oldfa;
    ch[old][o]=ch[x][o^1];fa[ch[x][o^1]]=old;
    ch[x][o^1]=old;fa[old]=x;
    update(x),update(old);
}
inline void splay(int x,int &k)
{
    while(x!=k)
    {
        if(fa[x]!=k)rotate(get(x)^get(fa[x])?x:fa[x],k);
        rotate(x,k);
    }
}
inline void insert(int x)
{
    //puts("");
    if(!root){root=++sz;size[sz]=cnt[sz]=1;key[sz]=x;return;}
    int now=root,o;
    while(1)
    {
        if(x==key[now])
        {
            ++cnt[now];
            splay(now,root);
            update(now);
            return;
        }
        o=x>key[now]?1:0;
        if(!ch[now][o])
        {
            ch[now][o]=++sz;
            size[sz]=cnt[sz]=1;
            key[sz]=x;fa[sz]=now;
            splay(sz,root);
            return;
        }
        else now=ch[now][o];
        //printf("%d %d %d %d
",now,fa[now],ch[now][0],ch[now][1]);
    }
}
inline int find_pos(int x)
{
    int now=root;
    while(1)
    {
        if(x==key[now]){return now;}
        if(x<key[now])now=ch[now][0];
        else now=ch[now][1];
    }
}
inline int pre()
{
    int now=ch[root][0];
    while(ch[now][1])now=ch[now][1];
    return now;
}
inline int nex()
{
    int now=ch[root][1];
    while(ch[now][0])now=ch[now][0];
    return now;
}
void del(int x)
{
    splay(find_pos(x),root);
    if(cnt[root]>1){--cnt[root];return;}
    if(!ch[root][0]&&!ch[root][1]){clear(root);root=0;return;}
    if(ch[root][0]&&ch[root][1])
    {
        int oldroot=root;
        splay(pre(),root);
        fa[ch[oldroot][1]]=root;
        ch[root][1]=ch[oldroot][1];
        clear(oldroot);
        update(root);
    }
    else
    {
        int o=ch[root][1]>0;
        root=ch[root][o];
        clear(fa[root]);
        fa[root]=0;
    }
}
inline int find_order_of_key(int x)
{
    int res=0,now=root;
    while(1)
    {
        if(x<key[now])now=ch[now][0];
        else
        {
            res+=size[ch[now][0]];
            if(x==key[now]){splay(now,root);return res+1;}
            res+=cnt[now];
            now=ch[now][1];
        }
    }
}
inline int find_by_order(int x)
{
    int now=root;
    while(1)
    {
        if(x<=size[ch[now][0]])now=ch[now][0];
        else
        {
            int temp=size[ch[now][0]]+cnt[now];
            if(x<=temp)return key[now];
            else{x-=temp;now=ch[now][1];}
        }
    }
}
void input()
{
    int T=read<int>();
    int opt,x;
    while(T--)
    {
        opt=read<int>();x=read<int>();
        if(opt==1)insert(x);
        else if(opt==2)del(x);
        else if(opt==3)printf("%d
",find_order_of_key(x));
        else if(opt==4)printf("%d
",find_by_order(x));
        else if(opt==5)
        {
            insert(x);
            printf("%d
",key[pre()]);
            del(x);
        }
        else if(opt==6)
        {
            insert(x);
            printf("%d
",key[nex()]);
            del(x);
        }
    }
}
int main()
{
    file();
    input();
    return 0;
}

洛谷P3391 splay模板
题目描述
您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：翻转一个区间，输出一行n个数字，表示原始序列经过m次变换后的结果

#include<bits/stdc++.h>
using namespace std;
typedef int sign;
typedef long long ll;
#define For(i,a,b) for(register sign i=(sign)a;i<=(sign)b;++i)
#define Fordown(i,a,b) for(register sign i=(sign)a;i>=(sign)b;--i)
const int N=1e5+5;
bool cmax(sign &a,sign b){return (a<b)?a=b,1:0;}
bool cmin(sign &a,sign b){return (a>b)?a=b,1:0;}
template<typename T>T read()
{
    T ans=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)&&ch!='-')ch=getchar();
    if(ch=='-')f=-1,ch=getchar();
    while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch-'0'),ch=getchar();
    return ans*f;
}
void file()
{
    #ifndef ONLINE_JUDGE
        freopen("splay.in","r",stdin);
        freopen("splay.out","w",stdout);
    #endif
}
int ch[N][2],fa[N],size[N],rev[N],root,sz;
inline int get(int x){return x==ch[fa[x]][1];}
inline void update(int x){size[x]=1+size[ch[x][0]]+size[ch[x][1]];}
inline void rotate(int x,int &k)
{
    int old=fa[x],oldfa=fa[old],o=get(x);
    if(k==old)k=x;
    else ch[oldfa][ch[oldfa][1]==old]=x;
    fa[x]=oldfa;fa[old]=x;fa[ch[x][o^1]]=old;
    ch[old][o]=ch[x][o^1];ch[x][o^1]=old;
    update(x),update(old);
}
inline void splay(int x,int &k)
{
    while(x!=k)
    {
        if(fa[x]!=k)rotate(get(x)^get(fa[x])?x:fa[x],k);
        //printf("%d %d
",x,k);
        rotate(x,k);
    }
}
#define mid ((l+r)>>1)
inline void build(int l,int r,int pre)
{
    if(l>r)return;
    ch[pre][mid>=pre]=mid;	
    fa[mid]=pre;size[mid]=1;
    if(l==r)return;
    build(l,mid-1,mid);build(mid+1,r,mid);
    update(mid);
}
#undef mid  
int n,m;
void input(){n=read<int>();m=read<int>();}
inline void rever(int x)
{
    swap(ch[x][0],ch[x][1]);
    rev[ch[x][0]]^=1;rev[ch[x][1]]^=1;
    rev[x]=0;
}
int find(int x)
{
    int now=root;
    while(1)
    {
        if(rev[now])rever(now);
        if(size[ch[now][0]]>=x)now=ch[now][0];
        else 
        {
            if(size[ch[now][0]]==x-1)return now;
            x=x-size[ch[now][0]]-1;
            now=ch[now][1];
        }
    }
}
void work()
{
    int l,r;
    root=(n+3)>>1;
    build(1,n+2,root);
    fa[root]=0;
    while(m--)
    {
        l=read<int>();r=read<int>();
        l=find(l);r=find(r+2);
        splay(l,root);splay(r,ch[l][1]);
        rev[ch[r][0]]^=1;
    }
}
void out(int x)
{
    if(rev[x])rever(x);
    if(ch[x][0])out(ch[x][0]);
    if(x>1&&x<n+2)printf("%d ",x-1);
    if(ch[x][1])out(ch[x][1]);
}
int main()
{
    file();
    input();
    work();
    out(root);
    return 0;
}

另外推荐一篇写得好的博客