Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
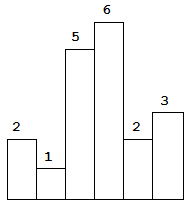
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
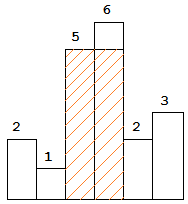
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given height = [2,1,5,6,2,3],
return 10.

1 class Solution { 2 public: 3 int largestRectangleArea(vector<int> &height) { 4 int max_area = 0; 5 stack<int> s; 6 height.push_back(0); 7 int i = 0; 8 while (i < height.size()) { 9 if (s.empty() || height[s.top()] < height[i]) { 10 s.push(i++); 11 } else { 12 int t = s.top(); 13 s.pop(); 14 max_area = max(max_area, 15 height[t] * (s.empty() ? i : i - s.top() - 1)); 16 } 17 } 18 return max_area; 19 } 20 };
O(n2)的算法还是很好想的,但是如果借用数据结构--栈,可以使复杂度降低。
从左向右扫描数组,如果bar递增,则入栈,遇到第一个下降的bar时,开始出栈,计算从该bar(不含)到栈顶元素(含)之间形成的矩形面积,直到遇到栈里第一个低于它的bar,此时可以继续向前扫描下一个元素。
栈里维护的是递增序列。
