题目来源:http://poj.org/problem?id=1054
题目大意:
有一种青蛙在晚上经过一片稻田,在庄稼上跳跃,会把庄稼压弯。这让农民很苦恼。我们希望通过分析青蛙跳跃的路径,找出对稻田造成最大损害的青蛙。青蛙跳跃时总是沿着直线并且步长均匀,但不同青蛙可能步长或方向不一样。如下图所示:
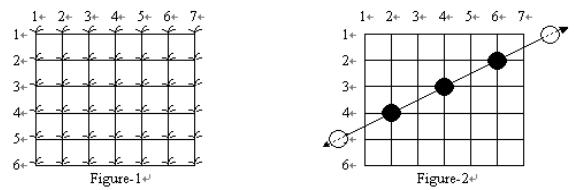
稻田庄稼是均匀地种在矩形网格交点处的,如下左图所示。青蛙总是会完全穿过这片稻田,也就是说从稻田外跳入并最终跳出稻田。如下右图所示。
有许多青蛙会穿过这片稻田,从庄稼上跳跃。我们可以知道那些庄稼被青蛙“踩”过,有的庄稼可能被多只青蛙踩过。但是我们并不知道青蛙的路径是怎样的。也就是说对于下左图的青蛙路径,我们只能知道下右图中的青蛙脚印点坐标。
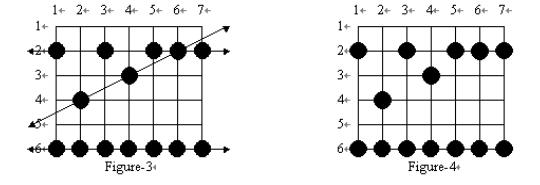
从Figure4,我们分析所有可能的青蛙路径,我们只关心脚印数大于3的路径,目标是找出所有可能的青蛙路径中脚印数最多的路径。Figure4对应的答案应该是7.
输入:第一行含两个整数R和C,表示稻田的行和列。1 <= R,C <= 5000.第二行为一个整数N,表示被压扁的庄稼数(即青蛙的脚印数),3 <= N <= 5000。接下来N行每行为一对整数,表示脚印坐标:行号r(1 <= r <= R)和列号c(1 <= c <= C),每个坐标只出现一次。
输出:一个整数表示穿过稻田留下脚印最多的青蛙的脚印数,如果找不到符合要求的青蛙路径输出0。
Sample Input
6 7 14 2 1 6 6 4 2 2 5 2 6 2 7 3 4 6 1 6 2 2 3 6 3 6 4 6 5 6 7
Sample Output
7
首先,暴力解决本题的思路是,遍历所有的脚印对,检查这两个脚印确定的直线可否穿过这对脚印形成青蛙路径,若可组成青蛙路径,记下路径的脚印数,然后找出路径上脚印数的最大值。这样做的问题是:一条路径上可能有很多点,那么每条路径都可能被计算多次,导致时间上的浪费。
可以用下面的方法来避免这个问题:我们假定青蛙在大方向上都是从稻田的一侧跳向另一侧,分别称为起点侧和终点侧。对于任意一条脚印路径,我们只在选取的脚印对(脚印对视为有序对,(i,j)和(j,i)为不同的脚印对)是路径上最靠近起点侧的两个脚印且i比j更靠近起点侧(或距离相等)时才检查一次这条路径(可以理解为 i 是青蛙跳进稻田第一步的脚印,j 是第二步的脚印),从而保证每条路径恰好被计算一次。
具体做法为:
首先,将所有脚印点进行排序。点的坐标(x, y), 排序策略为,首先按x由小到大排序,对于x相等的点再按列好从小到大排。
然后,对于排好序之后的脚印点,按顺序遍历脚印对时,假定第i个脚印点和第j个脚印点的坐标为(xi, yi), (xj, yj). 那么当 j > i 时,一定有xj >= xi。由前述的避免重复计算路径的策略,我们只计算所有的j>i的脚印对,即j一定是在经过i之后才到达的。
接下来,如何保证 i 和 j 恰好是最靠近起点侧的脚印(即青蛙跳进稻田后的第一步和第二步留下的脚印)?方法是:让青蛙“往回跳一步”,假定往回跳一步还在稻田内,那么有两种可能,一,回退一步的坐标是脚印点,那么这条直线可能形成路径,但不应该在遍历脚印点 i 和 j 时被计算,二,回退一步的坐标不是脚印点,那么这条直线不能穿过 i 和 j 形成青蛙路径,因为青蛙的步长是定值,无法直接从田外直接跳到 i。所以,只要青蛙回退一步的坐标仍然在田内,则这对脚印不可能符合要求,可以不用计算对应的路径。
再然后,并不是所有符合上面条件的 i 和 j 都会确定出一条可行的青蛙路径。(比如上面Figure4中的(2,2)和(3,4),所在的直线就不能组成可行路径)。判断方法就是假设路径可行,由已知的两个点已经知道青蛙的步长和方向,模拟青蛙向前跳,如果青蛙恰好沿脚印点跳出稻田,说明路径可行,否则不可行。
至此似乎已经可以比较好的解决这个这个问题了,不过还有一些优化的策略:
1.由于青蛙沿直线跳跃且一定会穿越整片稻田,那么脚印数一定有一个上界--稻田的长和宽中的较大值。若已经有某条路径达到了上界,则不需要再搜索和计算。
2.当确定一对要检查的脚印对 i 和 j 后,我们是假定这条路径可行,那么我们已经知道了假定的路径中青蛙的步长、方向和起点,所以我们可以预测出该条路径的脚印点数,如果脚印数小于已找到的最大值,则没有必要再检查这对点对应的路径了。
3.我们在排序时不一定要固定按行排或按列排。按长度方向较小的方向为主序来排序可以使排序发挥更大的作用。
按照上述的各种策略课将题目由TLE加快到100ms内完成。
最后要注意需要输出0的情况。

1 /////////////////////////////////////////////////////////// 2 // POJ1054 The Troublesome Frog 3 // Memory: 172K Time: 63MS 4 // Language: C++ Result: Accepted 5 ////////////////////////////////////////////////////////// 6 7 #include <cstdio> 8 #include <cstdlib> 9 10 using namespace std; 11 12 struct Plant { 13 int x, y; 14 }; 15 16 Plant foot_print[5001]; 17 int r, c, n; 18 int max_steps = 2; 19 20 int cmp_x(const void * a, const void * b) { 21 Plant * pa = (Plant *) a; 22 Plant * pb = (Plant *) b; 23 if (pa->x == pb->x) { 24 return pa->y - pb->y; 25 } else { 26 return pa->x - pb->x; 27 } 28 } 29 30 int cmp_y(const void * a, const void * b) { 31 Plant * pa = (Plant *) a; 32 Plant * pb = (Plant *) b; 33 if (pa->y == pb->y) { 34 return pa->x - pb->x; 35 } else { 36 return pa->y - pb->y; 37 } 38 } 39 40 int check_x(int j, int dx, int dy) { 41 int ans = 2; 42 Plant plant; 43 plant.x = foot_print[j].x + dx; 44 plant.y = foot_print[j].y + dy; 45 while (plant.x <= r && plant.y <= c && plant.y >= 1) { 46 if (bsearch(&plant, foot_print, n, sizeof(Plant), cmp_x)) { 47 plant.x += dx; 48 plant.y += dy; 49 ++ans; 50 } else { 51 return 0; 52 } 53 } 54 return ans; 55 } 56 57 int check_y(int j, int dx, int dy) { 58 int ans = 2; 59 Plant plant; 60 plant.x = foot_print[j].x + dx; 61 plant.y = foot_print[j].y + dy; 62 while (plant.x >= 1 && plant.x <= r && plant.y <= c) { 63 if (bsearch(&plant, foot_print, n, sizeof(Plant), cmp_y)) { 64 plant.x += dx; 65 plant.y += dy; 66 ++ans; 67 } else { 68 return 0; 69 } 70 } 71 return ans; 72 } 73 74 75 int main(void) { 76 scanf("%d%d%d", &r, &c, &n); 77 for (int i = 0; i < n; ++i) { 78 scanf("%d%d", &foot_print[i].x, &foot_print[i].y); 79 } 80 if (r > c) { 81 if (r > 2) { 82 qsort(foot_print, n, sizeof(Plant), cmp_x); 83 for (int i = 0; i < n - 2; ++i) { 84 for (int j = i + 1; j < n - 1; ++j) { 85 int dx = foot_print[j].x - foot_print[i].x; 86 int dy = foot_print[j].y - foot_print[i].y; 87 int px = foot_print[i].x - dx; 88 int py = foot_print[i].y - dy; 89 if (px >= 1 && py >= 1 && py <= c) { 90 continue; 91 } 92 px = foot_print[i].x + max_steps * dx; 93 if (px > r) { 94 break; 95 } 96 py = foot_print[i].y + max_steps * dy; 97 if (py < 1 || py > c) { 98 continue; 99 } 100 int ans = check_x(j, dx, dy); 101 if (ans > max_steps) { 102 max_steps = ans; 103 } 104 if (max_steps == r) { 105 printf("%d ", max_steps); 106 return 0; 107 } 108 } 109 } 110 } 111 } else if (c > 2) { 112 qsort(foot_print, n, sizeof(Plant), cmp_y); 113 for (int i = 0; i < n - 2; ++i) { 114 for (int j = i + 1; j < n - 1; ++j) { 115 int dx = foot_print[j].x - foot_print[i].x; 116 int dy = foot_print[j].y - foot_print[i].y; 117 int px = foot_print[i].x - dx; 118 int py = foot_print[i].y - dy; 119 if (px >= 1 && px <= r && py >= 1) { 120 continue; 121 } 122 py = foot_print[i].y + max_steps * dy; 123 if (py > c) { 124 break; 125 } 126 px = foot_print[i].x + max_steps * dx; 127 if (px < 1 || px > r) { 128 continue; 129 } 130 int ans = check_y(j, dx, dy); 131 if (ans > max_steps) { 132 max_steps = ans; 133 } 134 if (max_steps == c) { 135 printf("%d ", max_steps); 136 return 0; 137 } 138 } 139 } 140 } 141 if (max_steps <= 2) { 142 max_steps = 0; 143 } 144 printf("%d ", max_steps); 145 return 0; 146 }
