自底向上的归并排序算法

1、什么是自底向上的归并排序？

说到底，不管是前面说的自顶向下的归并排序还是现在讲的自底向上的归并排序，其实质都是归并。

来看看一个演示过程:

  这个就是待排序的数组序列

  先将数组序列以2个元素为一组分成4组，每个组内部分成2个子序列进行向上合并

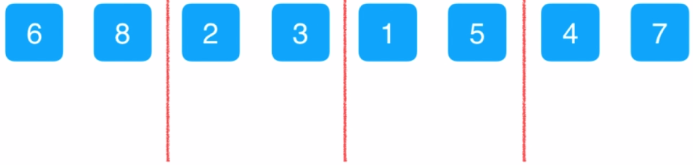  这是合并之后的效果

  然后以4个元素为一组分成2组，每个组内部分成2个子序列进行向上合并

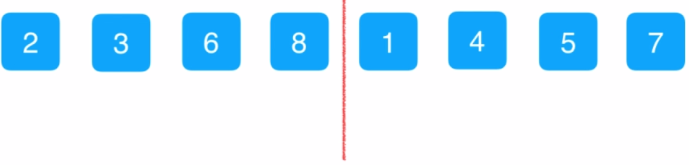  这是合并之后的效果

  然后以8个元素为一组分成1个组，每个组内部分成2个子序列进行向上合并

  最终整个序列编程有序的了

其实从这里看就可以知道，这个就好像是前面说的自顶向下排序过程中的后面一个过程。

2、时间复杂度

同自顶向下的归并排序相同，时间复杂度也是O(nlogn)级别。

3、算法的实现（基于C++）

#define   MIN(a, b)  ((a) < (b) ? (a) : (b))

/***************************** 自底向上的归并排序算法实现 ***********************************/
template<typename T>
void mergeSortBU (T arr[], int count)
{
    for (int size = 1; size <= count; size += size) {    // 外层循环把整个序列分成多个子序列，size表示一个子序列的元素个数，每一次循环以翻倍的形式增加    
        for (int i = 0; i + size < count; i += size + size) {  // 内层循环遍历所有子序列，以两个子序列为一组向上归并
            __merge<T>(arr, i, i + size - 1, MIN(i + size + size - 1, count - 1));  // 对两部分数据进行归并操作
        }
    }
}
/*******************************************************************************************/

4、性能测试（与经过优化过的自顶向下归并排序算法相比较）

测试数据量50000:

测试数据量100000:

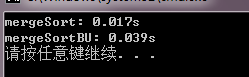
5、算法优化

其实跟自顶向下归并排序的优化算法是一样的

/***************************** 自底向上的归并排序算法实现 ***********************************/
template<typename T>
void mergeSortBU (T arr[], int count)
{
    for (int size = 1; size <= count; size += size) {    // 外层循环把整个序列分成多个子序列，size表示一个子序列的元素个数，每一次循环以翻倍的形式增加    
        for (int i = 0; i + size < count; i += size + size) {  // 内层循环遍历所有子序列，以两个子序列为一组向上归并
            if (MIN(i + size + size - 1, count - 1) - i < 40) { // 优化措施2
                __insertSortMG<T>(arr, i, MIN(i + size + size - 1, count - 1));   
                continue;
            }

            if (arr[i + size - 1] > arr[i + size]) {   // 优化措施1
                __merge<T>(arr, i, i + size - 1, MIN(i + size + size - 1, count - 1));  // 对两部分数据进行归并操作
            }   
        }
    }
}
/*******************************************************************************************/

优化过后的性能测试:

测试数据量50000:

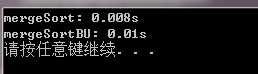
测试数据量100000:

总结: 从上面的数据可以看出来，经过优化之后，自底向上归并排序的性能得到了一个很大的提升，

但是还是比自顶向下归并排序慢，这个其实是有原因的，在这里不做分析。

还有一个值得一提的就是未经过优化的算法的代码可知，代码中没有使用数组的特性（使用索引找

到对应的元素），所以我们可以用自底向上归并排序对一个链表进行排序。