softmax 函数在机器学习中无处不在:当远离分类边界时,它假设似然函数有一个修正的指数尾。
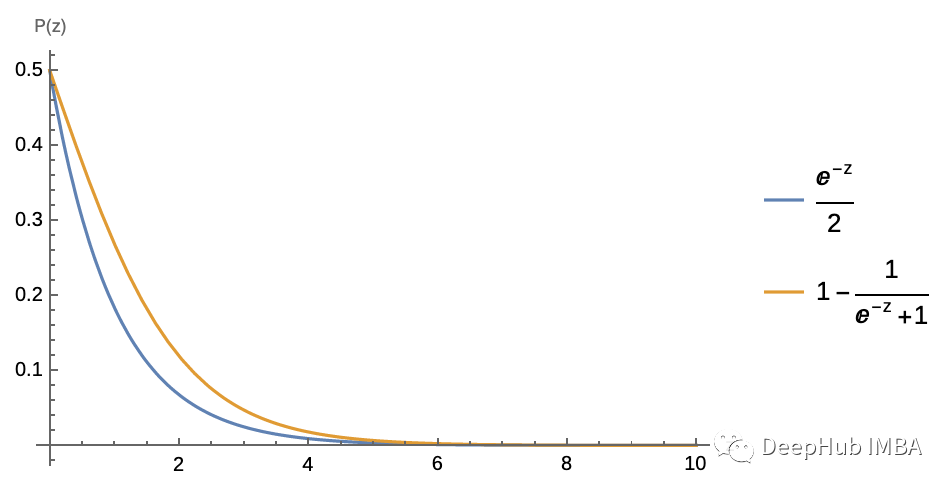
但是新数据可能不适合训练数据中使用的 z 值范围。如果出现新的数据点softmax将根据指数拟合确定其错误分类的概率;错误分类的机会并不能保证遵循其训练范围之外的指数(不仅如此——如果模型不够好,它只能将指数拟合到一个根本不是指数的函数中)。为避免这种情况将 softmax 函数包装在一个范围限制的线性函数中(将其概率限制在 1/n 和 1-1/n 之内)可能会有所帮助,其中 n 是训练数据中的样本数:
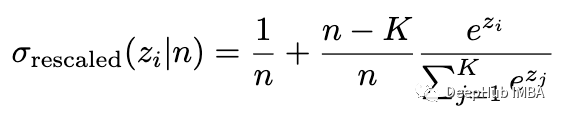
但是我们将通常的 softmax 函数视为最佳拟合曲线而不是似然函数,并根据(离散)高斯统计(首先用于两类)计算其误差:
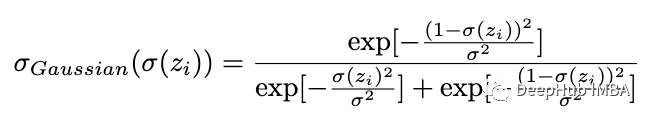
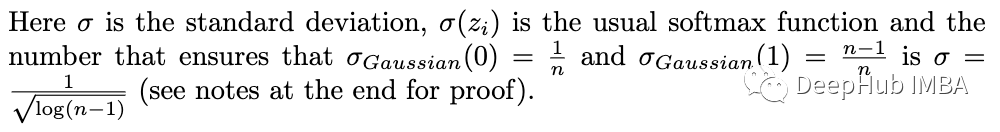
简化这个表达式后,我们得到:
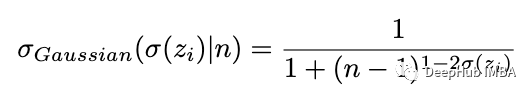
我们绘制原始函数以及 n=50,500,10000,1000000 的新高斯 softmax 函数:
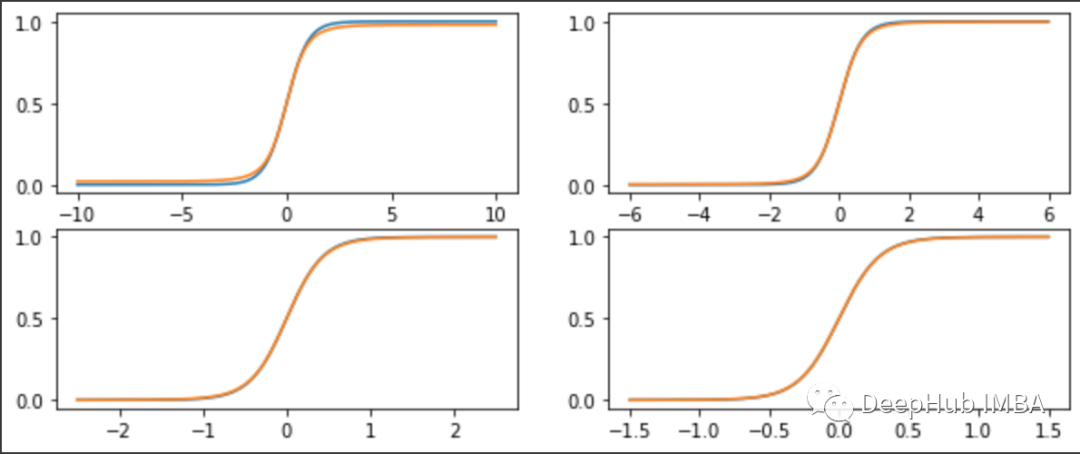
我们看到,该函数仅在 n<500 左右时出现不同(它是 log(n-1)/2)。其实并不是这样,我们绘制 n = 100 万的函数的对数:
完整文章:
https://avoid.overfit.cn/post/11690658dbc240c4bfb49a6c2e1b715f