Github
地址:https://github.com/deepYY/sudoku
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | 60 |
| Estimate | 估计这个任务需要多少时间 | 30 | 60 |
| Development | 开发 | 720 | 720 |
| Analysis | 需求分析 (包括学习新技术) | 120 | 480 |
| Design Spec | 生成设计文档 | 120 | 240 |
| Design Review | 设计复审 (和同事审核设计文档) | 60 | 120 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 60 | 60 |
| Design | 具体设计 | 60 | 60 |
| Coding | 具体编码 | 60 | 60 |
| Code Review | 代码复审 | 60 | 60 |
| Test | 测试(自我测试,修改代码,提交修改) | 120 | 360 |
| Reporting | 报告 | 10 | 10 |
| Test Report | 测试报告 | 10 | 10 |
| Size Measurement | 计算工作量 | 60 | 60 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 60 | 60 |
| 合计 | 1610 | 2300 |
解题思路
刚看到这题,因为要随机数独,所以我先去网上找了如何生成随机数的资料.然后我是想用二维数组存数独,然后从用随机数往里面依次从左到右,从上到下填数,在判断填入的数是否符合数独规则,符合就继续下一个,不符合就重新生成随机数.但发现刚开始填入没问题,但越到后面数独的规则就越来越束缚,所能填的数也越来越少,而且也会导致那个格只能填一个数,但填入那个数却不符合数独的情况存在.后来查阅数独这类算法的资料,发现数独回溯法,跟深度优先搜索一样,依次填下去,实在不行在回头重新填.在找资料的过程中也找到两篇很好的博客,一个是关于分治的思想来填入数独,将一个大的数独9*9的格,编号分成9个3*3的宫,先重数字1开始填到9个宫,边填边检查是否符合数独条件,这不仅省去了数独在一个宫的检查方式,而且在数字1和9的填入中也不需要回溯.我先是用这个方法实现随机数独,但后来因为有个固定一个数条件,我就用了我之前找资料时看到的另一篇博客的思想,是个用一个大小为9的一维数组来存1到9各不相同的随机数为一个随机序列,我就想将两者的方法结合,通过这组随机数来改变之前生成的随机数组从而满足题目要求.
参考博客:
- 1.http://blog.sina.com.cn/s/blog_a28e3dd90101e1i2.html
- 2.http://blog.csdn.net/peng_wu01/article/details/6026103
设计实现
- 用两个函数来当前判断填入的数是否符合数独的规则.
- 用一个函数来将没填入的格全填入9.
- 用一个函数通过回溯的方式来生成一个随机数独,用二维数组来存这个随机数独,这个函数有调用两个检查的函数.
- 用一个函数来生个一组大小为9的随机序列
- 用一个函数来改变生成的随机数独为满足题目要求的随机数独
- 用一个函数来数独查重(添加)
代码说明
void creat_Sudoku(int num, int number) { //建立数独、这里的num和number分别是要填的数和所填的块的编号
int x, y, l_flag, r_flag; //x和y存随机的位置,l_flag和r_flag是判断当前的位置是否符合数独规则
int t = 0; //记录重新随机的次数
int last1 = -1, last2 = -1; //上次的x和y的值用last1和last2来保存
if (num == 9) { //只剩9没填时,将格为0的全变为9
Sdk();
}
else {
while (true) {
x = rand() % 3 + 3 * (number / 3); //跟据块的编号,随机生成位置(x,y)
y = rand() % 3 + 3 * (number % 3);
if (Sudoku[x][y] != 0) { //当生成的位置有数时,重新随机,重新随机次数过多时,回溯
t++;
if (t == 8) {
flag = 2;
t = 0;
return;
}
continue;
}
if (Sudoku[x][y] == 0) {
if (last1 == x&&last2 == y) { //当生成的位置没数,但一直是这个位置,回溯
t++;
if (t == 8) {
flag = 2;
t = 0;
return;
}
continue;
}
last1 = x;
last2 = y;
Sudoku[x][y] = num;
r_flag = check_row(x, y);
l_flag = check_line(x, y);
if (r_flag == 1 || l_flag == 1) {
Sudoku[x][y] = 0;
t++;
if (t < 8) continue;
else {
t = 0;
flag = 2;
return;
}
}
if (r_flag == 0 && l_flag == 0) {
if (number != 8) {
creat_Sudoku(num, number + 1); //填入的这个数满足数独条件,到下一个数
if (flag == 2) { //当发生回溯,重新生成随机数
Sudoku[x][y] = 0;
flag = 0;
continue;
}
else break;
}
else {
creat_Sudoku(num + 1, 0); //填入的这个数满足数独条件,到下一个数
if (flag == 2) {
Sudoku[x][y] = 0;
flag = 0;
continue;
}
else break;
}
}
}
}
}
}
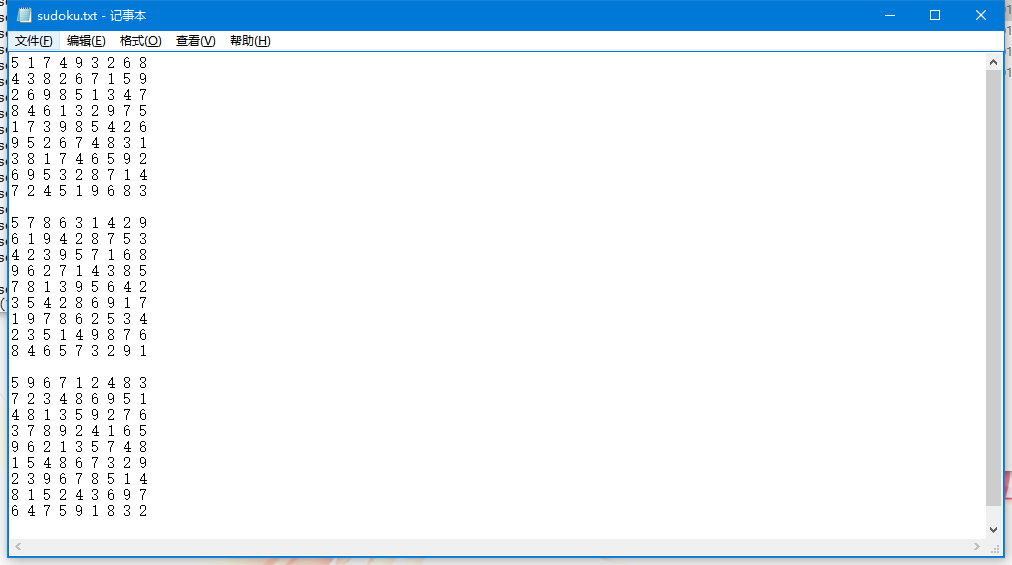
测试运行
测试:

结果:
性能分析

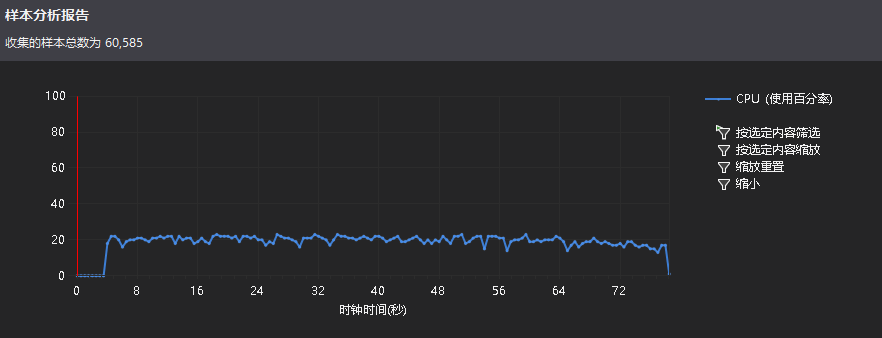
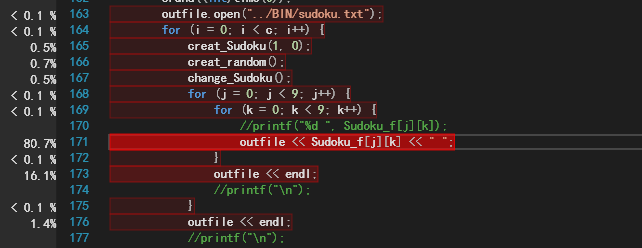
从上图中可以看出,在创建数独的函数creat_Sudoku()和以及去改变数独的函数chang_Sudoku()所占用的比较小,占用较大的主要在于将数独输出到sudoku.txt的函数上,我本想在输出到txt文件上优化,但现在遇到一个问题,当把ofstream 定义到全局时sudoku.exe文件就会停止工作,还在寻找解决方案。
多谢助教的提醒,将数独一次性输出,果然在输出函数上有了很大的优化。

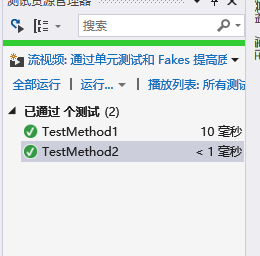
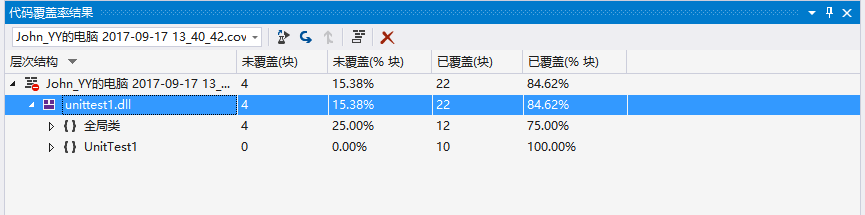
单元测试