题面

思路
这是一类套路题,相似的套路是这道题
具体而言,为了体现选择1到9中某一个数只能选一个,并且每个有自己的不同贡献,我们把每个格子拆成10个点,其中九个点分别代表1-9,一个点作为“缓冲点”
然后把S-T中间连上这n*m条链
然后,本题中的另外一个限制是相邻的两个格子和不超过给定值,这里需要在相邻格子对应的链之间连边
具体而言,我们需要这样分配不同的链:
我们把原图的矩阵黑白染色
对于黑色格子对应的链(简称黑色链),连法是:
$S-9-8-7-6-5-4-3-2-1-0-T$
对于白色链则是:
$S-0-1-2-3-4-5-6-7-8-9-T$
其中编号为$i$的点的入边边权为$10-i$,0号点的入边边权为inf
之所以这里是$10-i$,是因为本题如果用割的角度思考的话,应该要求的是最大割,这里把边权反过来就可以求最小割了
对于两个相邻的黑白格子$(u,v)$,设限制为$k$,那么如此连边:
对于所有的$(i+j)=k$,连边$(v,j)->(u,i)$,边权为inf
此处$(v,j)$表示$v$的链上编号为$j$的点
画个图大概就是这样:
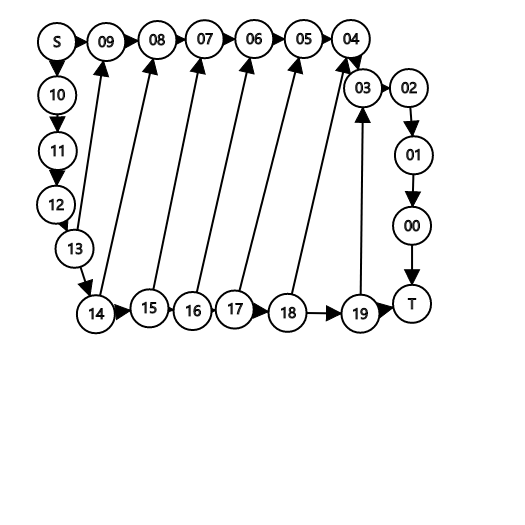
这里展示的是$k=12$时的情况
注意所有的边都是白色链往黑色链连的
这样连的意义何在呢?
我们考虑一种情况:在上面的那个图里我们选择割掉0809之间的边,它的边权是10-8=2
那么,此时如果我们在白色链上割掉的是14以后的边,那么仍然存在一条从S到14到08到T的路径,这并不是一个合法的割
所以,我们的算法为了最小化割值,会选择14以前的边
这样我们就达成了我们需要的和值限制
于是我们这样连边以后,跑一个S-T最小割,再用nm10减去这个最小割,就得到了可能的最大和值
Code
#include<iostream>
#include<cassert>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define id(i,j,k) num[i][j][k]
using namespace std;
inline int read(){
int re=0,flag=1;char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') re=(re<<1)+(re<<3)+ch-'0',ch=getchar();
return re*flag;
}
int n,m,d[110][110],r[110][110],num[110][110][10],first[50010],cnte=-1;
struct edge{
int to,next,w;
}a[200010];
inline void add(int u,int v,int w){
if(w<=10) w=10-w;
a[++cnte]=(edge){v,first[u],w};first[u]=cnte;
a[++cnte]=(edge){u,first[v],0};first[v]=cnte;
}
int dep[50010],cur[50010],q[50010],head,tail;
bool bfs(int s,int t){
int i,u,v;head=0,tail=1;
for(i=s;i<=t;i++) dep[i]=-1,cur[i]=first[i];
dep[s]=0;q[0]=s;
while(head<tail){
u=q[head++];
for(i=first[u];~i;i=a[i].next){
v=a[i].to;if(~dep[v]||!a[i].w) continue;
dep[v]=dep[u]+1;q[tail++]=v;
}
}
return ~dep[t];
}
int dfs(int u,int t,int lim){
if(u==t||!lim) return lim;
int i,v,f,flow=0;
for(i=first[u];~i;i=a[i].next){
v=a[i].to;
if(dep[v]==dep[u]+1&&(f=dfs(v,t,min(lim,a[i].w)))){
a[i].w-=f;a[i^1].w+=f;
flow+=f;lim-=f;
if(!lim) return flow;
}
}
return flow;
}
int dinic(int s,int t){
int re=0;
while(bfs(s,t)) re+=dfs(s,t,1e9);
return re;
}
int main(){
memset(first,-1,sizeof(first));
n=read();m=read();int i,j,k,s=0,t=n*m*10+1;
for(i=1;i<=n;i++) for(j=1;j<=m;j++) for(k=0;k<=9;k++) num[i][j][k]=k*n*m+((i-1)*m+j);
for(i=1;i<n;i++)
for(j=1;j<=m;j++)
d[i][j]=read();
for(i=1;i<=n;i++)
for(j=1;j<m;j++)
r[i][j]=read();
for(i=1;i<=n;i++){
for(j=1;j<=m;j++){
if((i+j)%2){
//9->0
add(s,id(i,j,0),1e9);add(id(i,j,0),id(i,j,9),9);
for(k=8;k>=1;k--) add(id(i,j,k+1),id(i,j,k),k);
add(id(i,j,1),t,1e9);
for(k=9;k>=1;k--){
//limit from former nodes
if((i>1)&&(d[i-1][j]-k<=9)) add(id(i-1,j,max(0,d[i-1][j]-k)),id(i,j,k),1e9);
if((j>1)&&(r[i][j-1]-k<=9)) add(id(i,j-1,max(0,r[i][j-1]-k)),id(i,j,k),1e9);
//limit to latter nodes
if((i<n)&&(d[i][j]-k<=9)) add(id(i+1,j,max(0,d[i][j]-k)),id(i,j,k),1e9);
if((j<m)&&(r[i][j]-k<=9)) add(id(i,j+1,max(0,r[i][j]-k)),id(i,j,k),1e9);
}
}
else{
add(s,id(i,j,0),1e9);
for(k=1;k<=9;k++) add(id(i,j,k-1),id(i,j,k),k);
add(id(i,j,9),t,1e9);
}
}
}
printf("%d
",n*m*10-dinic(s,t));
}