莫队,顾名思义,就是由莫队长发明的算法【雾】
实际上它的发明者莫涛菊苣的确进队了【雾】进的还是国家队【大雾】
不带修改的序列上莫队:
考虑这样一个问题:有一个长度为n的序列,可能会有重复的数,有m个询问,每次问一段区间有多少不同的数
n和m都在30000左右
显然暴力处理不了,线段树又会炸空间
等等,暴力处理不了?
那我们来把暴力写的优美一点吧【雾】
考虑最原始的暴力,就是扫一遍询问区间然后输出,效率O(n)
但是这么做很浪费,因为可能有些询问的重复区间很大,相当于重复统计了,降低了时间效率
我们就从这方面下手优化
首先,一个非常显然的想法就是,每次我们在两个询问区间之间“转移”,加上没算的,减掉不用算的
但是这样还有个问题:万一他出在序列两头的询问很多,那不就卡掉你了?
没关系,我们有排序大法,理论上我们只要把这些询问序列按照某个顺序排好就行了
但是怎么排这m个二元组(i,j)呢?
我们看,每两个二元组之间转移需要花费的时间就是这两个二元组在平面直角坐标系上表示的点之间的曼哈顿距离
所以其实我们可以跑一个曼哈顿距离MST【反正我是不会做的】,但是这样显然太麻烦了
能不能代码效率高一点?
莫涛队长给出了答案
他说:我们把n的序列分成sqrt(n)块,每块sqrt(n)个元素,然后按照左端点所在的块的顺序为第一关键字、右端点为第二关键字排序
这样排出来的询问序列可以在O(nsqrt(n))的时间解决
证明是这样的:
首先,左端点的总移动距离,显然不会超过O(nsqrt(n)),因为都是按照块分好了的啊
而右端点,在左端点在同一个块中是有序的,最多转移O(n),有sqrt(n)个块,所以右端点转移也是O(nsqrt(n))的
总时间效率O(nsqrt(n))
需要注意的是,莫队因为有一个排序的过程,所以一定是离线的,包括后面要讲的修改和树上莫队都是离线算法
一道例题:SDOI2009 HH的项链
问的其实就是上面那个问题
题解链接在这:题解
带单点修改的序列上莫队
修改来了,原始莫队瑟瑟发抖.....因为上文中提到的“重复计算”不复存在了!
那怎么处理呢?显然我们还是要用某种方法最小化修改对这个优美的暴力带来的影响
那我们继续排序【hhhh】
这回增加第三关键字ch表示当前询问在第几个修改之后,同时把第二关键字改成右端点所在的块
这样我们会发现总效率是O(n*sqrt(n)*sqrt(n))的(╯‵□′)╯︵┻━┻这不没区别吗!!!
别急,我们更改一下分块方式,令一个块的大小变成n^(2/3),一共有n^(1/3)个块
这样的话,左端点的转移一共是O(n*n^(2/3)) == O(n^(5/3)),右端点转移相同
而=修改带来的影响分散了,一共最多O(n*n^(2/3)),也是O(n^(5/3))
所以这样分块的总时间效率是O(n^(5/3))的,足以过10000的问题了
真是个优美的暴力呢
一道例题:[国家集训队]数颜色
据说是莫队亲自出的题(ΩДΩ)
树上带与不带修改莫队
树上?????
别扯了,树又不是序列.....
这是我看到树上莫队的第一想法
但是,我们考虑在树上询问不同颜色的个数的问题,发现这么多询问下来,重复的依然很多,莫队的“消除重复”思想依然可以实现
而且谁说树上不能序列化了?dfs序听了这话想打人......
先考虑对子树的询问:一棵树, 每个节点都有颜色, 每次问你一个子树中有多少不同的颜色
我们发现一棵子树在dfs序上一定是连续的
那我们把dfs序求出来,再做标准莫队的过程就没问题了 ,甚至可以带上修改
但是,树上提问可不止子树询问,我们遇到的更多是树上两点之间的路径的询问
但是这种时候一条路径在dfs序上可就不是连续的了
难道我们树剖?常数卡死人......
不急,我们来推导一下怎么转移吧
我们考虑这样一个树,图示是树的一部分(也就是这两个询问涉及的部分)
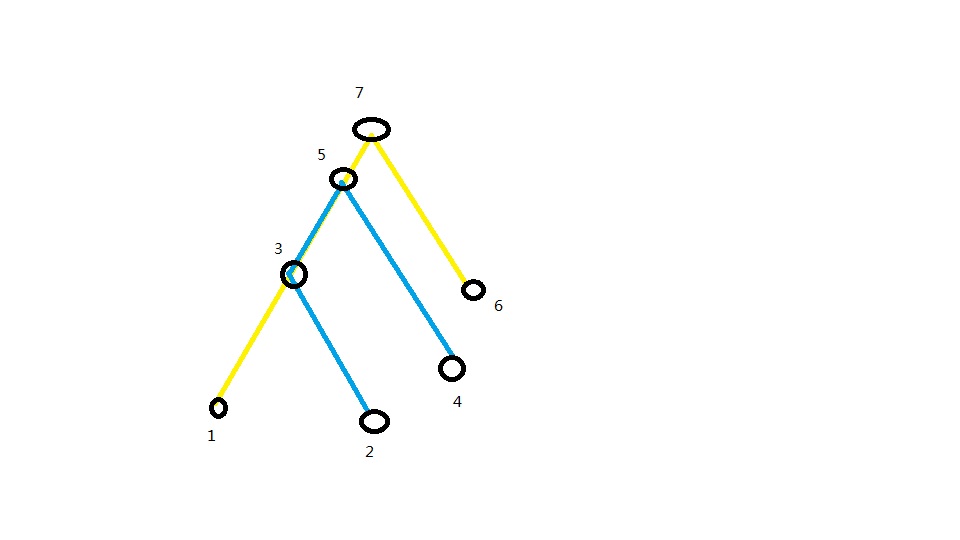
我们当前处理出来的是询问(1,6)的答案,也就是这条黄色路径
我们下一个要求的是蓝色路径(2,4)的答案
这种情况下我们发现,其实每次增加的就是lca(1,2)到2,以及lca(4,6)到4的那些节点
同时lca(1,2)到1,以及lca(4,6)到6的路径上的节点要去掉
诶?
那岂不是可以求出两个lca,然后把这两对点路径上除了lca的点的状态都反过来就可以了?
别急这只是一种情况,但是这个结论,实际上是对的
我们说的多种情况,无非就是两个lca在树上的位置关系
而这一位置关系,实际上取决于两个询问的两端节点的lca的位置关系(有点绕,一定要看清楚)
而这个关系要么就是父亲-儿子,要么就是毫不相干
上面那种情况就是父亲-儿子,此时lca(1,2) and lca(4,6)中间的那些节点不会受到影响
而两个原lca如果相离的话,我们可以发现中间的那段节点被处理了两次,也就是反转再反转,实际上没有动
因此这个转移方式是合法的
还有一个问题:两条路径上的lca是否收到影响呢?
关于这一点,我们发现,lca(1,2)与lca(4.6),在任何情况下都不应该被碰到,因此我们不能改变它们的状态
但是有一个点是需要注意的:就是新的询问两端的lca
这个点在前面的转移中会被反转掉,因此我们需要把它反转,统计答案,再转回去以免影响下一个询问
同样,这样做的时间效率,在每一块分sqrt(n)时,是在O(nsqrt(n))左右,带了修改也是O(n^(5/3))
一道例题:[WC2013]糖果公园,是一个带修改的树上莫队
本来想放bzoj3757数苹果的,那是一道不带修改的题目,但是那道题被权限了......
总结:
莫队,正如前面所讲的一样,是一个“优美的暴力”,这说明它的本质其实就是暴力扫一遍修改。
但是,莫涛队长看到了原来的暴力方法中可供修改的部分:重复操作
这一思想其实在很多地方都可以用到
比如网络流算法dinic的当前弧优化,甚至dinic算法本身都是在减免重复操作
很多时候,竞赛题里面需要自己yy算法的那些内容,也就是让你减少一些重复的操作
因此学了莫队,要从莫队本身的思维出发,拓展到每一道题目中、每一个算法中去