1.归类:
- 聚类(clustering) 属于非监督学习 (unsupervised learning)
- 无类别标记(class label)
2.举例:
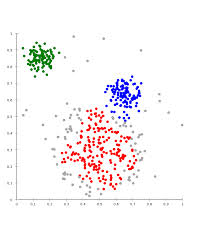
3. K-means 算法:
3.1 Clustering 中的经典算法,数据挖掘十大经典算法之一
3.2 算法接受参数 k ;然后将事先输入的n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一
聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
3.3 算法思想:
以空间中k个点(可随机选取)为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心
的值,直至得到最好的聚类结果
3.4 算法描述:
(1)适当选择c个类的初始中心;
(2)在第k次迭代中,对任意一个样本,求其到c各中心的距离,将该样本归到距离最短的中心所在
的类;
(3)利用均值等方法更新该类的中心值;
(4)对于所有的c个聚类中心,如果利用(2)(3)的迭代法更新后,值保持不变,则迭代结束,
否则继续迭代。
3.5 算法流程:

输入:k, data[n];
(1) 选择k个初始中心点,例如c[0]=data[0],…c[k-1]=data[k-1];
(2) 对于data[0]….data[n], 分别与c[0]…c[k-1]比较,假定与c[i]差值最少,就标记为i;
(3) 对于所有标记为i点,重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数;
(4) 重复(2)(3),直到所有c[i]值的变化小于给定阈值。
4.举例:
4.1 流程图:
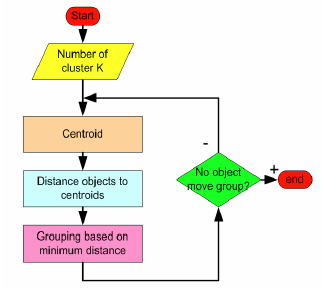
4.2 一个药物分类的例子:

四中药物给予了 weight index 和 pH 两个特征。
在二维坐标系中的分布如下:
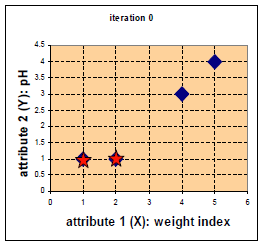
D0为第一次迭代,第一行为4个点到c1的距离,第二行为4个点到c2的距离。
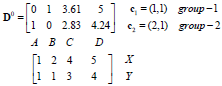
G0为第一次迭代后的归类情况,将各点到c1、c2的距离进行比较,哪个的距离小就为哪一类。
归类如下:c1为第一类,c2、c3、c4为第二类。
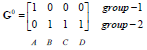
第二类的中心点更新如下:

重新计算中心点如下(星为中心点):(若该类中的点变化,则更新该类的中心点;否则不更新)
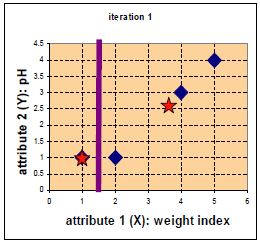
第二次迭代。
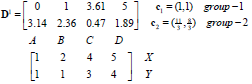
G1为第二次迭代后的归类情况。
归类如下:c1、c2为第一类,c3、c4为第二类。
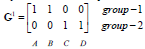
更新第一类、第二类的中心点如下:
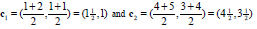
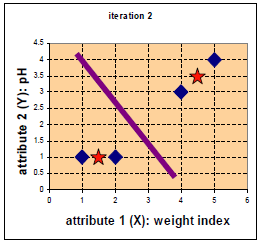

归类没有发生变化(达到终止条件)
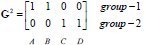
停止。

优点:速度快,简单
缺点:最终结果跟初始点选择相关,容易陷入局部最优,需直到k值