POJ 3549 GSM phone（圆+扫描线+最短路）

题目意思是求起点s到终点s的最短路，但是只能在圆的内部和边上走。一种可以想到的方法就是求出所有的交点，然后两两连边并验证合法性，但是这样的交点数规模有n²。

我们可以观察发现，我们在圆求并构成的图形中，在其内部的点是不可能成为最短路上的点，只可能是沿着边上的点擦着经过，所以我们需要把在圆内部的所有点都给扣掉，同样可以证明这样的点的规模只有n个，接下来只需要暴力连边，但是连边的时候需要验证这样的点对是否沿着直线可达。我是直接将这条线段暴力和所有圆求交点，左侧端点计为1，右侧端点计为-1，然后用类似于扫描线的做法sort一遍，最后判断线段的两端是否被这个区间包含即可。

最后跑一边dijk就求出答案。

这个方法感觉不是很好.... 还有比我快20倍的orz... 

如果扣的是灰色点那么规模有n²

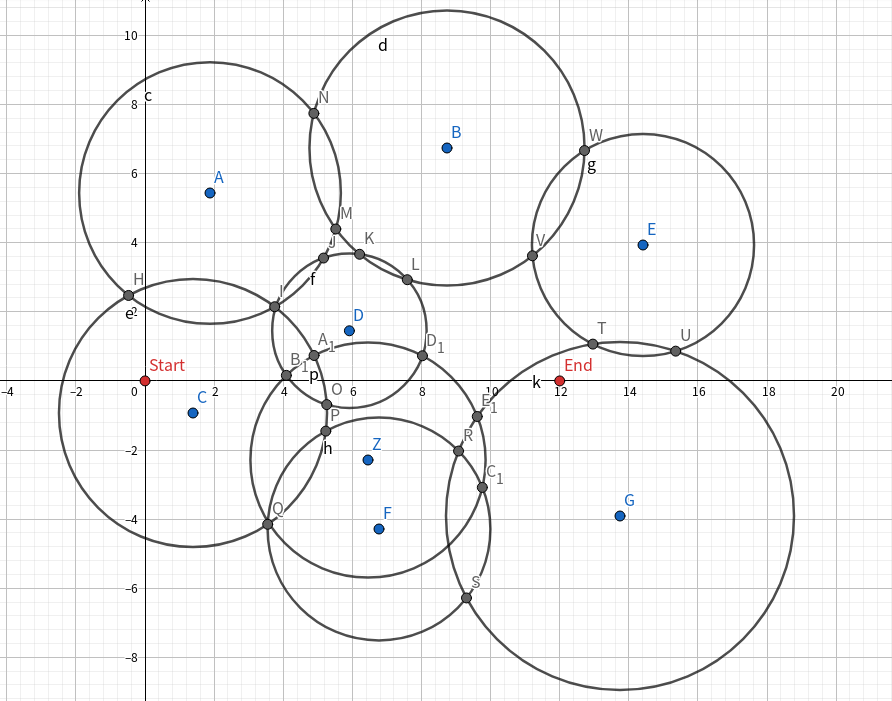
如果是外侧点只有n个，绿色点即为可用点，红色和橙色为两条路，则最短路必然擦过外侧点或者起点终点直接相连

 

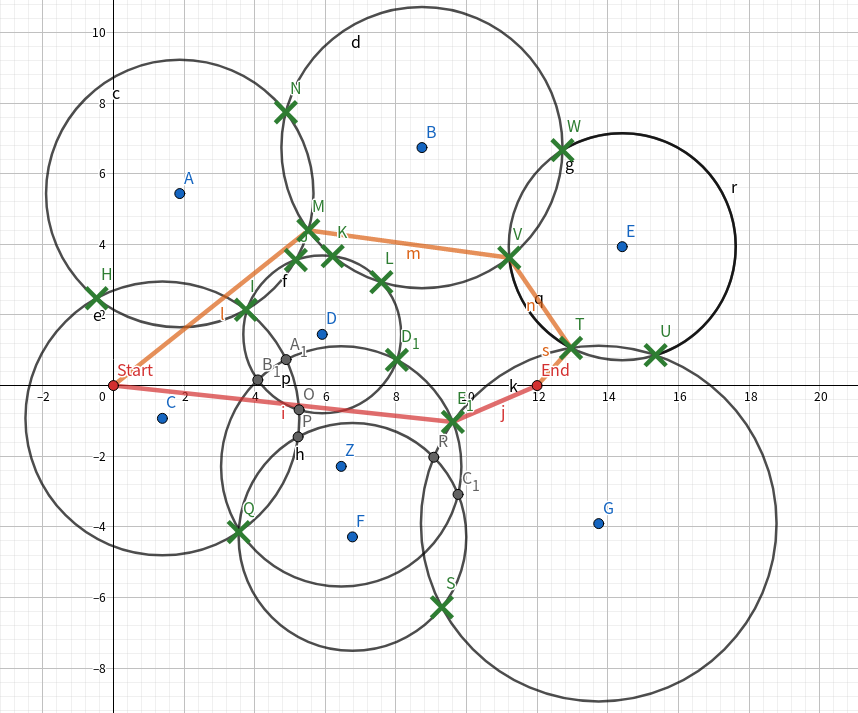
//      ——By DD_BOND

//#include<bits/stdc++.h>
//#include<unordered_map>
//#include<unordered_set>
#include<functional>
#include<algorithm>
#include<iostream>
//#include<ext/rope>
#include<iomanip>
#include<climits>
#include<cstring>
#include<cstdlib>
#include<cstddef>
#include<cstdio>
#include<memory>
#include<vector>
#include<cctype>
#include<string>
#include<cmath>
#include<queue>
#include<deque>
#include<ctime>
#include<stack>
#include<map>
#include<set>
#include<cassert>

#define fi first
#define se second
#define pb push_back
#define MP make_pair

#pragma GCC optimize(3)
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")

using namespace std;

typedef long double db;
typedef long long ll;
typedef pair<db,db> Pd;
typedef pair<int,int> P;
typedef pair<ll,ll> Pll;

const db eps=1e-8;
const int MAXN=1e5+10;
const db pi=acos(-1.0);
const ll INF=0x3f3f3f3f3f3f3f3f;

inline int dcmp(db x){
    if(fabs(x)<eps) return 0;
    return (x>0? 1: -1);
}

inline db Sqrt(db x){
    return x>0? sqrt(x): 0;
}

inline db sqr(db x){ return x*x; }

struct Point{
    db x,y;
    Point(){ x=0,y=0; }
    Point(db _x,db _y):x(_x),y(_y){}
    void input(){
        double _x,_y;
        scanf("%lf%lf",&_x,&_y);
        x=_x,y=_y;
    }
    void output(){ printf("%.2f %.2f
",(double)x,(double)y); }
    friend istream &operator >>(istream &os,Point &b){
        os>>b.x>>b.y;
        return os;
    }
    friend ostream &operator <<(ostream &os,Point &b){
        os<<b.x<<' '<<b.y;
        return os;
    }
    bool operator ==(const Point &b)const{
        return (dcmp(x-b.x)==0&&dcmp(y-b.y)==0);
    }
    bool operator !=(const Point &b)const{
        return !((dcmp(x-b.x)==0&&dcmp(y-b.y)==0));
    }
    bool operator <(const Point &b)const{
        return (dcmp(x-b.x)==0? dcmp(y-b.y)<0 : x<b.x);
    }
    db operator ^(const Point &b)const{     //叉积
        return x*b.y-y*b.x;
    }
    db operator *(const Point &b)const{     //点积
        return x*b.x+y*b.y;
    }
    Point operator +(const Point &b)const{
        return Point(x+b.x,y+b.y);
    }
    Point operator -(const Point &b)const{
        return Point(x-b.x,y-b.y);
    }
    Point operator *(db a){
        return Point(x*a,y*a);
    }
    Point operator /(db a){
        return Point(x/a,y/a);
    }
    db len2(){  //长度平方
        return sqr(x)+sqr(y);
    }
    db len(){   //长度
        return Sqrt(len2());
    }
    Point change_len(db r){ //转化为长度为r的向量
        db l=len();
        if(dcmp(l)==0)  return *this;  //零向量
        return Point(x*r/l,y*r/l);
    }
    Point rotate_left(){    //逆时针旋转90度
        return Point(-y,x);
    }
    Point rotate_right(){   //顺时针旋转90度
        return Point(y,-x);
    }
};

inline db cross(Point a,Point b){   //叉积
    return a.x*b.y-a.y*b.x;
}

inline db dot(Point a,Point b){ //点积
    return a.x*b.x+a.y*b.y;
}

inline db dis(Point a,Point b){ //两点的距离
    Point p=b-a;    return p.len();
}

struct Line{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e):s(_s),e(_e){} //两点确定直线
    void input(){
        s.input();
        e.input();
    }
    db length(){    //线段长度
        return dis(s,e);
    }
};

inline db point_to_line(Point p,Line a){   //点到直线距离
    return fabs(cross(p-a.s,a.e-a.s)/a.length());
}

inline Point projection(Point p,Line a){       //点在直线上的投影
    return a.s+(((a.e-a.s)*dot(a.e-a.s,p-a.s))/(a.e-a.s).len2());
}

struct Circle{
    Point p;
    db r;
    Circle(){}
    void input(){
        p.input();
        double _r;
        scanf("%lf",&_r);
        r=_r;
    }
};

inline int relation(Point p,Circle a){ //点和圆的位置关系  0:圆外    1:圆上   2:圆内
    db d=dis(p,a.p);
    if(dcmp(d-a.r)==0)  return 1;
    return (dcmp(d-a.r)<0? 2: 0);
}

inline int relation(Line a,Circle b){  //直线和圆的位置关系  0:相离   1:相切   2:相交
    db p=point_to_line(b.p,a);
    if(dcmp(p-b.r)==0)  return 1;
    return (dcmp(p-b.r)<0? 2: 0);
}

inline int relation(Circle a,Circle v){    //圆和圆的位置关系  1:内含  2:内切  3:相交   4:外切   5:相离
    db d=dis(a.p,v.p);
    if(dcmp(d-a.r-v.r)>0)   return 5;
    if(dcmp(d-a.r-v.r)==0)  return 4;
    db l=fabs(a.r-v.r);
    if(dcmp(d-l)>0)     return 3;
    if(dcmp(d-l)==0)    return 2;
    return 1;
}

inline int circle_intersection(Circle a,Circle v,Point &p1,Point &p2){ //两个圆的交点
    int rel=relation(a,v);                                      //返回交点个数，保存在引用中
    if(rel==1||rel==5)  return 0;
    db d=dis(a.p,v.p);
    db l=(d*d+a.r*a.r-v.r*v.r)/(2*d);
    db h=Sqrt(a.r*a.r-l*l);
    Point tmp=a.p+(v.p-a.p).change_len(l);
    p1=tmp+((v.p-a.p).rotate_left().change_len(h));
    p2=tmp+((v.p-a.p).rotate_right().change_len(h));
    if(rel==2||rel==4)  return 1;
    return 2;
}

inline int line_circle_intersection(Line v,Circle u,Point &p1,Point &p2){  //直线和圆的交点
    if(!relation(v,u))  return 0;                                   //返回交点个数，保存在引用中
    Point a=projection(u.p,v);
    db d=point_to_line(u.p,v);
    d=Sqrt(u.r*u.r-d*d);
    if(dcmp(d)==0){
        p1=a,p2=a;
        return 1;
    }
    p1=a+(v.e-v.s).change_len(d);
    p2=a-(v.e-v.s).change_len(d);
    return 2;
}

typedef pair<db,int>pdi;
typedef pair<Point,int> pd;

vector<pdi>edge[MAXN];

db d[MAXN];
pd st[MAXN];
bool mark[MAXN];
Circle circle[MAXN];
Point s,t,it1,it2,inter[MAXN],point[MAXN];

priority_queue<pdi,vector<pdi>,greater<pdi> >q;

bool cmp(pd a,pd b){
    if(a==b)    return a.se>b.se;
    return a<b;
}

int main(void){
    s.input();  t.input();
    int n,m=1,cnt=1;  scanf("%d",&n);
    for(int i=1;i<=n;i++)   circle[i].input();
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++){
            int p=relation(circle[i],circle[j]);
            if(p==2||p==3||p==4){
                circle_intersection(circle[i],circle[j],it1,it2);
                point[m++]=it1,point[m++]=it2;
            }
        }
    sort(point+1,point+m);
    m=unique(point+1,point+m)-point;
    for(int i=1;i<m;i++)
        for(int j=1;j<=n;j++)
            if(relation(point[i],circle[j])==2){
                mark[i]=1;
                break;
            }
    for(int i=1;i<m;i++)
        if(mark[i]==0)
            point[cnt++]=point[i];
    m=cnt;  point[0]=s,point[m]=t;
    for(int i=0;i<=m;i++)
        for(int j=i+1;j<=m;j++){
            int p=0;
            Line l(point[i],point[j]);
            Point p1=point[i],p2=point[j];
            if(p2<p1)   swap(p1,p2);
            for(int k=1;k<=n;k++){
                Circle c=circle[k];
                if(relation(l,c)){
                    line_circle_intersection(l,c,it1,it2);
                    if(it2<it1) swap(it1,it2);
                    st[p++]=pd(it1,1);
                    st[p++]=pd(it2,-1);
                }
            }
            int found=0;
            sort(st,st+p,cmp);
            for(int k=0,sum=0,start=0;k<p;k++){
                sum+=st[k].se;
                if(sum==0){
                    if(!(p1<st[start].fi)&&!(st[k].fi<p2)) found=1;
                    start=k+1;
                }
            }
            if(found){
                edge[i].pb(pdi(l.length(),j));
                edge[j].pb(pdi(l.length(),i));
            }
        }
    for(int i=1;i<=m;i++)   d[i]=1e20;
    q.push(pdi(0,0));
    while(!q.empty()){
        pdi p=q.top();  q.pop();
        if(dcmp(d[p.se]-p.fi)<0)   continue;
        for(int i=0;i<edge[p.se].size();i++){
            int v=edge[p.se][i].se;
            db val=edge[p.se][i].fi;
            if(dcmp(d[p.se]+val-d[v])<0){
                d[v]=d[p.se]+val;
                q.push(pdi(d[v],v));
            }
        }
    }
    printf("%.5f
",(double)d[m]);
    return 0;
}