首先能想到的是至少有一对相邻点或者中间间隔一个点的点对满足轴对称,那么接下来只需要枚举剩下的点对是否满足至多移动一个点可以满足要求。
第一种情况,对于所有点对都满足要求,那么Yes。
第二种情况,有一个点不满足要求,那么显然这种情况只可能是奇数点的时候才出现,那么只需要将这个点移到对称轴上则满足要求,那么Yes。
第三种情况,有两个点不满足要求,然后我们需要枚举这两个点对应的对称点是否满足要求,对于其中一个点的对称点判断他是否和之前所有点重合,以及判断这个点是否在对称轴上。
这样还不够,还需要考虑对于对称轴两边的可能的对应的对称点,他们是不是在对应一侧,如果两个点都不在对应的一侧,说明这两个点自交,则不能满足要求,直接跳过。
多注意细节吧,现场wa到自闭。
数据:
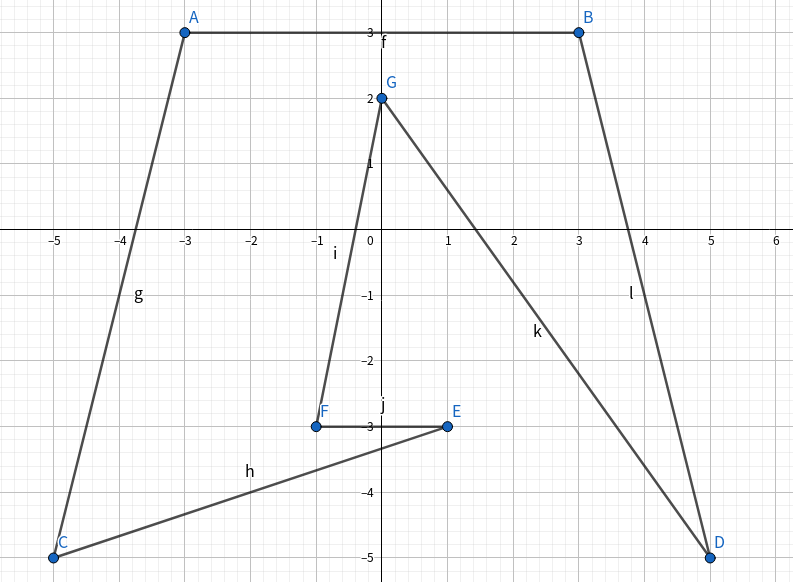
5 -100 -100 0 0 -100 100 2 -1 100 1 N 7 -3 3 -5 -5 1 -3 -1 -3 0 2 5 -5 3 3 N
附图说明:
1 // ——By DD_BOND 2 3 //#include<bits/stdc++.h> 4 //#include<unordered_map> 5 //#include<unordered_set> 6 #include<functional> 7 #include<algorithm> 8 #include<iostream> 9 //#include<ext/rope> 10 #include<iomanip> 11 #include<climits> 12 #include<cstring> 13 #include<cstdlib> 14 #include<cstddef> 15 #include<cstdio> 16 #include<memory> 17 #include<vector> 18 #include<cctype> 19 #include<string> 20 #include<cmath> 21 #include<queue> 22 #include<deque> 23 #include<ctime> 24 #include<stack> 25 #include<map> 26 #include<set> 27 28 #define fi first 29 #define se second 30 #define MP make_pair 31 #define pb push_back 32 33 typedef long long ll; 34 35 using namespace std; 36 37 const int MAXN=1e3+10; 38 const double eps=1e-12; 39 const double pi=acos(-1.0); 40 const ll INF=0x3f3f3f3f3f3f3f3f; 41 42 inline int dcmp(double x){ 43 if(fabs(x)<eps) return 0; 44 return (x>0? 1: -1); 45 } 46 47 inline double sqr(double x){ return x*x; } 48 49 struct Point{ 50 double x,y; 51 Point(){ x=0,y=0; } 52 Point(double _x,double _y):x(_x),y(_y){} 53 void input(){ scanf("%lf%lf",&x,&y); } 54 bool operator ==(const Point &b)const{ 55 return (dcmp(x-b.x)==0&&dcmp(y-b.y)==0); 56 } 57 Point operator +(const Point &b)const{ 58 return Point(x+b.x,y+b.y); 59 } 60 Point operator -(const Point &b)const{ 61 return Point(x-b.x,y-b.y); 62 } 63 Point operator *(double a){ 64 return Point(x*a,y*a); 65 } 66 Point operator /(double a){ 67 return Point(x/a,y/a); 68 } 69 double len2(){ //长度平方 70 return sqr(x)+sqr(y); 71 } 72 Point rotate_left(){ //逆时针旋转90度 73 return Point(-y,x); 74 } 75 }; 76 77 inline double cross(Point a,Point b){ //叉积 78 return a.x*b.y-a.y*b.x; 79 } 80 81 inline double dot(Point a,Point b){ //点积 82 return a.x*b.x+a.y*b.y; 83 } 84 85 struct Line{ 86 Point s,e; 87 Line(){} 88 Line(Point _s,Point _e):s(_s),e(_e){} //两点确定直线 89 }; 90 91 int relation(Point p,Line l){ //点和向量关系 1:左侧 2:右侧 3:在线上 92 int c=dcmp(cross(p-l.s,l.e-l.s)); 93 if(c<0) return 1; 94 else if(c>0) return 2; 95 else return 3; 96 } 97 98 Point projection(Point p,Line a){ //点在直线上的投影 99 return a.s+(((a.e-a.s)*dot(a.e-a.s,p-a.s))/(a.e-a.s).len2()); 100 } 101 102 Point symmetry(Point p,Line a){ //点关于直线的对称点 103 Point q=projection(p,a); 104 return Point(2*q.x-p.x,2*q.y-p.y); 105 } 106 107 int vis[MAXN]; 108 vector<Line>st; 109 Point point[MAXN]; 110 111 int main(void){ 112 int T; scanf("%d",&T); 113 while(T--){ 114 int n,ans=0; scanf("%d",&n); 115 for(int i=0;i<n;i++) point[i].input(); 116 for(int i=0;i<n&&!ans;i++){ 117 int s=i,t=(i+1)%n; 118 Point mid=(point[s]+point[t])/2,vec=(point[s]-point[t]).rotate_left(); 119 Line line(mid,mid+vec); 120 int num=0,error=0; 121 memset(vis,0,sizeof(vis)); 122 while(!vis[s]&&!vis[t]){ 123 vis[s]=1,vis[t]=1; 124 Point p1=(point[s]+point[t])/2,dir=(point[s]-point[t]).rotate_left(); 125 Point p2=p1+dir; 126 if(dcmp(cross(point[i]-mid,vec))*dcmp(cross(point[s]-mid,vec))<0&&dcmp(cross(point[(i+1)%n]-mid,vec))*dcmp(cross(point[t]-mid,vec))<0) error=1; 127 if(relation(p1,line)==3&&relation(p2,line)==3){ 128 if(s!=t) num+=2; 129 else num++; 130 } 131 s=(s-1+n)%n,t=(t+1)%n; 132 } 133 if(error) continue; 134 if(num+1>=n) ans=1; 135 else if(num+2==n){ 136 s=i,t=(i+1)%n; 137 memset(vis,0,sizeof(vis)); 138 while(!vis[s]&&!vis[t]){ 139 vis[s]=1,vis[t]=1; 140 Point p1=(point[s]+point[t])/2,vec=(point[s]-point[t]).rotate_left(); 141 Point p2=p1+vec; 142 if(relation(p1,line)!=3||relation(p2,line)!=3){ 143 if(relation(point[s],line)!=3&&relation(point[t],line)!=3){ 144 int f1=0,f2=0; 145 Point s1=symmetry(point[s],line),s2=symmetry(point[t],line); 146 for(int j=0;j<n;j++) 147 if(point[j]==s1) 148 f1=1; 149 for(int j=0;j<n;j++) 150 if(point[j]==s2) 151 f2=1; 152 if(!f2||!f1) ans=1; 153 } 154 break; 155 } 156 s=(s-1+n)%n,t=(t+1)%n; 157 } 158 } 159 } 160 for(int i=0;i<n&&!ans;i++){ 161 int s=(i-1+n)%n,t=(i+1)%n; 162 Point mid=(point[s]+point[t])/2,vec=(point[s]-point[t]).rotate_left(); 163 Line line(mid,mid+vec); 164 int num=0,error=0; s=t=i; 165 memset(vis,0,sizeof(vis)); 166 while(!vis[s]&&!vis[t]){ 167 vis[s]=1,vis[t]=1; 168 Point p1=(point[s]+point[t])/2,dir=(point[s]-point[t]).rotate_left(); 169 Point p2=p1+dir; 170 if(dcmp(cross(point[(i-1+n)%n]-mid,vec))*dcmp(cross(point[s]-mid,vec))<0&&dcmp(cross(point[(i+1)%n]-mid,vec))*dcmp(cross(point[t]-mid,vec))<0) error=1; 171 if(relation(p1,line)==3&&relation(p2,line)==3){ 172 if(s!=t) num+=2; 173 else num++; 174 } 175 s=(s-1+n)%n,t=(t+1)%n; 176 } 177 if(error) continue; 178 if(num+1>=n) ans=1; 179 else if(num+2==n){ 180 s=t=i; 181 memset(vis,0,sizeof(vis)); 182 while(!vis[s]&&!vis[t]){ 183 vis[s]=1,vis[t]=1; 184 Point p1=(point[s]+point[t])/2,vec=(point[s]-point[t]).rotate_left(); 185 Point p2=p1+vec; 186 if(relation(p1,line)!=3||relation(p2,line)!=3){ 187 if(relation(point[s],line)!=3&&relation(point[t],line)!=3){ 188 int f1=0,f2=0; 189 Point s1=symmetry(point[s],line),s2=symmetry(point[t],line); 190 for(int j=0;j<n;j++) 191 if(point[j]==s1) 192 f1=1; 193 for(int j=0;j<n;j++) 194 if(point[j]==s2) 195 f2=1; 196 if(!f2||!f1) ans=1; 197 } 198 break; 199 } 200 s=(s-1+n)%n,t=(t+1)%n; 201 } 202 } 203 } 204 if(ans) puts("Y"); 205 else puts("N"); 206 } 207 return 0; 208 }