最大流
基本概念
最大流问题(Maximum Flow Problem)是一种组合最优化问题,是网络流的基础。把问题抽象成一个有向图,从源点到汇点的每一条边都有一个最大容量,指这条边可以流过的流量最大值。问题要求的就是从源点到汇点的最大流量。注意和最长路的区别在于,它的流量可以通过多个路径流到汇点。
在求解问题之前,我们先来认识一些概念;
容量网络:我们刚才说的有向图G,即每条边都有一个最大容量的网络;
弧:就是网络中的边;
弧分四类:(设有一条弧流量为h(u,v),最大容量为c)
1,饱和弧,即h(u,v)= c;
2,非饱和弧,即h(u,v)< c;
3,非零弧,即h(u,v)< 0;
4,零弧,即h(u,v)= 0;
流量:一条弧实际所流过的流量;
可行流:满足条件1和2的一个网络流f:
1,流量限制,即每条弧的流量不能超过最大容量;
2,平衡条件限制,即每条弧流入的流量一定等于它流出的流量;
(特别地,如果一个网络上所有流量均为0,则称之为零流)
链:即从点u到u1,u1到u2,……,un到v的一条序列,其中每两个相邻的点都要连有一条弧,设L是网络G中一条从源点S到汇点T的链,则约定S到T的方向为正方向,但链中的弧方向不一定要和正方向相同。我们称链中和正方向相同的弧为正向弧,反之为反向弧;
增广路:设f是G中的一个可行流,设L是从S至T的一条链,若:
L中所有正向弧均为非饱和弧,且所有反向弧均为非零弧,
那么这条链就称为f的一条增广路,沿着增广路改进的操作叫做增广;
残留容量:即在当前的可行流中弧h(u,v)的最大容量c减去已流流量f(u,v)的残余流量,记为su(u,v);
残余网络:即残余容量组成的网络,设残余网络G’,则对于G中的每一条弧h(u,v),若它是一条非饱和弧,则在G’中有一条弧h’(u,v),其最大容量c’(u,v)=c(u,v)-h(u,v),若它是一条非零弧,则在G’中有一条弧h”(v,u),其容量为c(u,v)。
问题求解
解决最大流有很多种解法,如EK、Isap、FF等,不过最有名的(主要是我们神圣的陈老师讲了的)就是dinic算法,我们今天也只介绍这一种,其他的有兴趣的童鞋可以自行百度。
dinic
学习dinic之前,我们先引入一个概念:层次图;
层次图就是分层图,一个点到源点的最短距离就叫做它的“层次”,分层图中“层次”相同的点为一层。建立分层图有一个好,就是同一层的点不可能在同一条链中,这样在找增广路时可以省去很多重复计算。
所以dinic的基本思路就是不断地根据残余网络建立层次图,然后在层次图中dfs找增广路,直到无法增广为止,这样运行速度就会快很多。下面就来看一下具体的解决精髓:反向边
反向边
我们为什么要反向边呢?看下面的一个例子(源点是1,汇点是4): 
我们可以很快的找到一个增广路1-2-3-4,增加流量为1,得到流如下: 
可这时我们发现,弧(1,2)和(3,4)都已经是饱和弧,再也找不到增广路了,而最大流却明显不是1,是2,即同时走1-2-4和1-3-4。那么问题出在哪里了呢?
问题就是我们没有给算法“后悔”的机会,它找完一个增广路后就没有改变原来2-3-4而走2-4的操作。那么怎么解决呢?暴力回溯?等着TLE吧。。。
所以dinic(其实所有最大流的算法都是)用了一个非常神奇的东东来解决这个问题:反向边。
反向边,就是对于网络G中的每条弧h(u,v)都加入一条反向弧h(v,u),初始最大容量为c(u,v)。
而在每次增广的时候,就将增广路上每一段容量减少n,同时将反向弧容量增加n。
继续看刚才的例子,加入反向边后,网络流修改成如下: 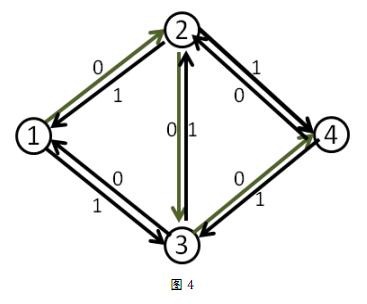
那么此时再找,就可以找到1-3-2-4这条增广路,最终最大流量为2。 
可是这样做为什么是对的呢?因为当我们第二次增广走过反向边3-2时就相当于把2-3这条正向边所用的流量给“退流”了,即不走2-3-4而改走从2出发的其它路,即2-4,最终流量也是一样的。(注意2-4是必定存在的,因为如果没有2-4的话就不会有1-3-2-4这条增广路)同时3-4的流量就变到了1-3-4这条路上,2-3这条边正向反向流量均为1,就相互抵消了,相当于没有流量。
这就是反向边的基本思想,它通过“退流”的方式,给了算法后悔的机会。下面直接上代码:
代码(POJ1273——模板题)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 struct edge{ 7 int y,r,next,op; 8 }a[401]; 9 int head[201],q[5001],level[201],ans=0,x,y,z,n,m,vs,vt,tot=0; 10 void add(int x,int y,int z){ 11 a[++tot].y=y; 12 a[tot].r=z; 13 a[tot].next=head[x]; 14 head[x]=tot; 15 a[tot].op=tot+1; 16 a[++tot].y=x; 17 a[tot].r=0; 18 a[tot].next=head[y]; 19 head[y]=tot; 20 a[tot].op=tot-1; 21 } 22 bool bfs(){ 23 int u,tmp,v,f=1,r=1; 24 memset(level,0,sizeof(level)); 25 q[f]=vs; 26 level[vs]=1; 27 while(f<=r){ 28 v=q[f]; 29 tmp=head[v]; 30 while(tmp!=-1){ 31 u=a[tmp].y; 32 if(a[tmp].r&&!level[u]){ 33 level[u]=level[v]+1; 34 q[++r]=u; 35 if(u==vt)return true; 36 } 37 tmp=a[tmp].next; 38 } 39 f++; 40 } 41 return false; 42 } 43 int dfs(int v,int num){ 44 int value,flow,tmp,u,ans=0; 45 if(v==vt||!num)return num; 46 tmp=head[v]; 47 while(tmp!=-1){ 48 u=a[tmp].y; 49 value=a[tmp].r; 50 if(level[u]==level[v]+1){ 51 flow=dfs(u,min(value,num)); 52 if(flow){ 53 a[tmp].r-=flow; 54 a[a[tmp].op].r+=flow; 55 ans+=flow; 56 num-=flow; 57 if(!num)break; 58 } 59 } 60 tmp=a[tmp].next; 61 } 62 return ans; 63 } 64 int main(){ 65 scanf("%d%d",&n,&m); 66 vs=1; 67 vt=m; 68 memset(head,255,sizeof(head)); 69 for(int i=1;i<=n;i++){ 70 scanf("%d%d%d",&x,&y,&z); 71 add(x,y,z); 72 } 73 while(bfs()){ 74 ans+=dfs(1,2147483647); 75 } 76 printf("%d",ans); 77 return 0; 78 }
时间复杂度
dinic算法算是所有解决最大流问题的算法中效率最高的一种,证明比较复杂,这里直接给出复杂度:
最坏情况时间复杂度:$O(V^{2}E)$;
期望时间复杂度:$O(min(V^{frac{3}{2}},E^{frac{1}{2}})*E)$;
最好时间复杂度(二分图):$O(sqrt{V}E)$;