参考:
对一个无序数组,根据某个关键字排序。
划分方法
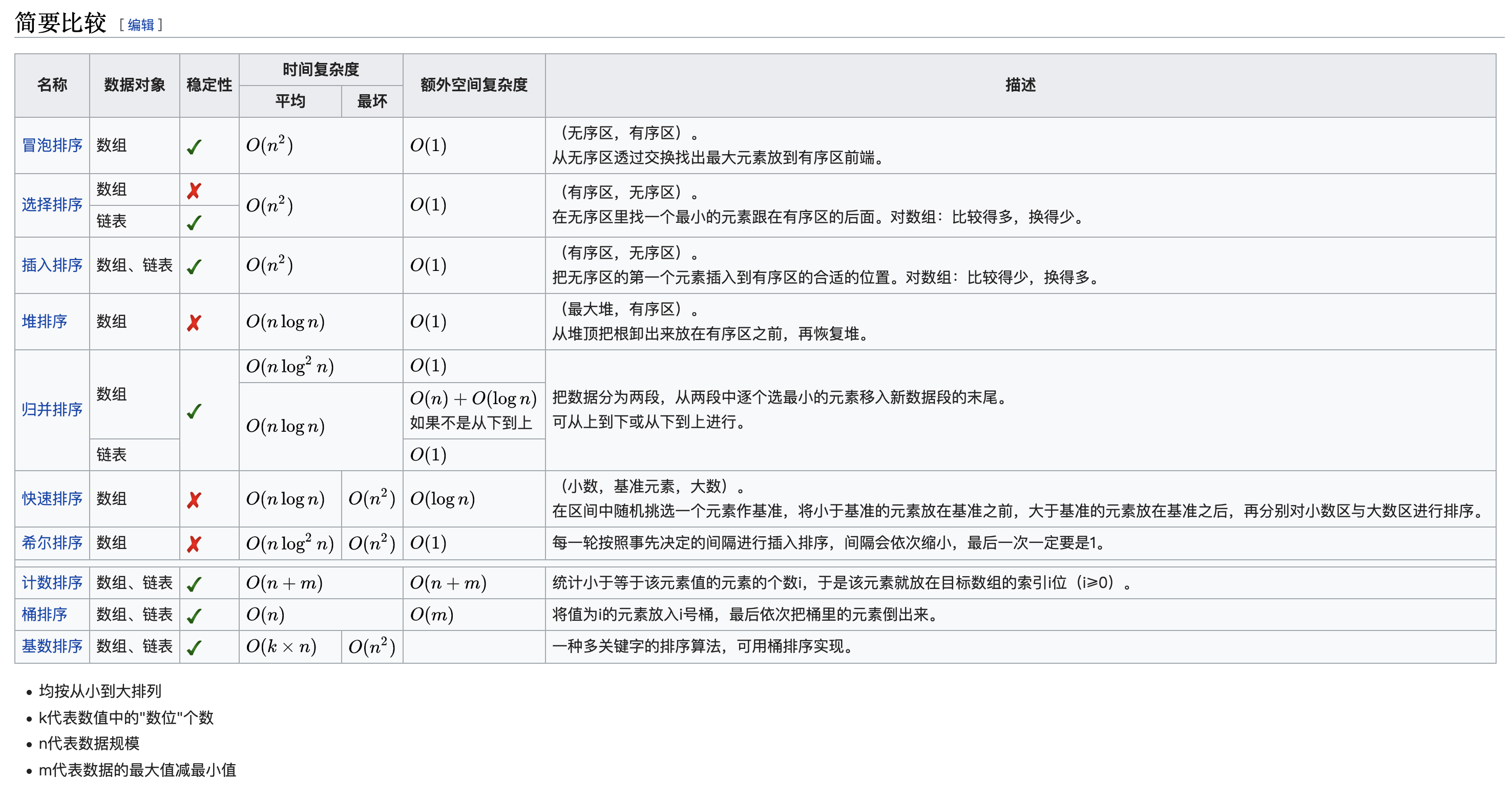
排序算法划分方法有:稳定性,内外排序,时空复杂度
按照稳定性划分,稳定排序,如果a原本在b前面,而a=b,排序之后a仍然在b的前面;而不稳定可能出现在b之后。
按照内外排序划分,内排序,所有排序操作都在内存中完成;外排序 :由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
按照时空复杂度划分,时间复杂度是指运行时间,空间复杂度运行完一个程序所需内存的大小。
1.冒泡
思路:每一轮排序,每次循环从头开始比较,但尾部根据i变化,length-i-1或者length-i,相当于每次当前尾部位置固定,每次循环选出当前轮最大的放后面,大的往数组尾部移动,小的往前挪
时空分析: 时间/空间 O(n^2)
稳定性:稳定
内排排序: 内排序
python
# 1.冒泡排序-稳定-内排序-时间复杂度O(n^2), 空间复杂度O(n^2)
def bubbleSort(nums: [int]) -> [int]:
for i in range(len(nums)):
for j in range(1, len(nums)-i):
if nums[j-1] > nums[j]:
nums[j-1], nums[j] = nums[j], nums[j-1]
return nums
golang
// 1.bubble
func bubbleSort(nums []int) []int {
for i := range nums {
for j:=1;j<len(nums)-i;j++ {
if nums[j-1] > nums[j] {
nums[j-1], nums[j] = nums[j], nums[j-1]
}
}
}
return nums
}
2.选择
思路:每一轮排序,每次循环从头开始比较,不断把小的往前面推,大的被选择交换到后面,每一轮选出当轮最小的,相当于i固定位置,但交换后的值肯定是当轮最小的
时空分析: 时间/空间 O(n^2)
稳定性:数组实现不稳定,链表稳定
内排排序: 内排序
python
# 2.选择排序-不稳定-内排序-时空O(n^2)
def selectSort(nums: [int]) -> [int]:
length = len(nums)
for i in range(length):
for j in range(i, length):
if nums[i] > nums[j]:
nums[i], nums[j] = nums[j], nums[i]
return nums
golang
// 2.select
func selectSort(nums []int) []int {
length := len(nums)
for i := range nums {
for j:=i;j<length;j++ {
if nums[i] > nums[j] {
nums[i], nums[j] = nums[j], nums[i]
}
}
}
return nums
}
3.插入
思路:每一轮排序,会把当前遍历的元素之前的那些元素排序,使得每一轮循环结束,当前元素及其前面元素都排好序,后面再循环,相当于把某元素插入到合适位置
e.g. nums = [1,2,3,2,6,4,7], 当前遍历的元素为下标3的元素2,后面的6/4/7不动,该元素2不断与其前面排好序的元素比较,直到找到下标2合适的插入位置,
即下标1/2的元素2/3之间,所以此轮循环比较后,nums=[1,2,2,3,6,4,7],后面遍历重复此过程。
时空分析: 时间/空间 O(n^2)
稳定性:数组稳定
内排排序: 内排序
python
# 3.插入排序-稳定-内排序-时空O(n^2)
def insertSort(nums: [int]) -> [int]:
length = len(nums)
for i in range(1, length):
while i > 0 and nums[i-1] > nums[i]:
nums[i-1], nums[i] = nums[i], nums[i-1]
i -= 1
return nums
golang
// 3.insert
func insertSort(nums []int) []int {
length := len(nums)
for i:=0;i<length;i++ {
for j:=i;j>0;j-- {
if nums[j-1] > nums[j] {
nums[j-1], nums[j] = nums[j], nums[j-1]
}
}
}
return nums
}
4.希尔-插入排序升级版
思路:定义增量序列gap,通常取[1,2,4,...2^(k-1)], 循环增量序列,从大的增量开始递减,每个增量序列使用时,遍历从gap到length的元素,每次比较交换i-gap与i位置的元素, 比较后i = i-gap,直到gap=0为止
时空分析: 时间/空间 O(n^2), 与增量序列有关,[1,2,4,8...]最坏O(n^2), [1,3,5,7,9...]最坏O(n^1.5), [1,5,19,41,109,...] -> O(n^1.3),详情查阅《数据结构与算法分析》
稳定性:不稳定
内排排序: 内排序
python
# 4.希尔排序-不稳定-内排序-时空O(n^2)
def shellSort(nums: [int]) -> [int]:
length = len(nums)
gap = length >> 1
while gap:
for i in range(gap, length):
while i-gap >= 0 and nums[i-gap] > nums[i]:
nums[i-gap], nums[i] = nums[i], nums[i-gap]
i -= gap
gap >>= 1
return nums
golang
// 4.shell
func shellSort(nums []int) []int {
length := len(nums)
gap := length >> 1
for gap > 0 {
for i:=gap;i<length;i++ {
j := i
for j-gap >= 0 && nums[j-gap] > nums[j] {
nums[j-gap], nums[j] = nums[j], nums[j-gap]
j -= gap
}
}
gap >>= 1
}
return nums
}
5.归并
思路:递归实现,如length=10 的数组, 先拆分为前5后5的子数组,前5的子数组拆分为更小的子数组前2后3,前2的子数组拆分为更小的前1后1的子数组,合并left,right的元素各1的数组,返回,接下来处理下标为2-4的子数组,其实也是被拆分的排序后合并,一次递归出栈,最后合并前5元素的left和后5元素的right子数组,排序后合并,拆分的过程不断压栈,合并的过程不断出栈:
- 将数组对半拆分为 n/2 的子数组
- 对子数组进行排序
- 合并两个子数组
时空分析: 时间/空间 O(nlogn)
稳定性:稳定
内排排序: 内排序/外排序(解决数据量大的问题)
python
# 5.归并排序
def mergeSort(nums: [int]) -> [int]:
def merge(left: [int], right: [int]) -> [int]:
res = []
i, j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
res.append(left[i])
i += 1
else:
res.append(right[j])
j += 1
res += left[i:]
res += right[j:]
return res
# 递归终止条件
if len(nums) <= 1:
return nums
mid = len(nums) >> 1
# 分左右子数组
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
# 合并
return merge(left, right)
golang
// 5.merge
func mergeSort(nums []int) []int {
// 递归终止
if len(nums) <= 1 {
return nums
}
// 拆分与合并
mid := len(nums) >> 1
left := mergeSort(nums[:mid])
right := mergeSort(nums[mid:])
return merge(left, right)
}
func merge(left, right []int) []int {
res := make([]int, len(left)+len(right))
l, r, i := 0, 0, 0
for l < len(left) && r < len(right) {
if left[l] <= right[r] {
res[i] = left[l]
l++
} else {
res[i] = right[r]
r++
}
i++
}
copy(res[i:], left[l:])
copy(res[i+len(left)-l:], right[r:])
return res
}
6.快速排序
快速排序是选取一个“哨兵”(pivot),将小于pivot放在左边,把大于pivot放在右边,分割成两部分,并且可以固定pivot在数组的位置,在对左右两部分继续进行排序。
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。
思路:
- 步骤1:从数列中挑出一个元素,称为 “基准”(pivot );
- 步骤2:重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 步骤3:递归地(recursive)把小于基准值元素的子数组和大于基准值元素的子数组排序
时空分析: 时间 O(nlogn)
稳定性:不稳定
内排排序: 内排序
python
# 6.快速排序-不稳定-内排序-时空O(nlogn)
def quickSort(nums: [int]) -> [int]:
length = len(nums)
def quick(left: int, right: int) -> [int]:
if left > right:
return nums
pivot = left
i, j = left, right
while i < j: # while循环的操作在于寻找pivot位置并交换元素,最终使得pivot为基准,分割左右半区元素,继续递归
while i < j and nums[j] >= nums[pivot]: # 大于pivot对应元素时, j--,实现右指针左移,直到 j <= i(往往相遇时相等) 或者 nums[j] < nums[pivot]
j -= 1
while i < j and nums[i] <= nums[pivot]: # 小于等于pivot对应元素时,i++,实现左指针右移,直到 i >= j(往往相遇时相等) 或者 num[i] > nums[pivot]
i += 1
nums[i], nums[j] = nums[j], nums[i] # 当 i=j 时,已经跳出上面两个while循环,即左右指针相遇,或者(j的元素小于等于pivot && i的元素大于pivot),肯定需要交换不同位置元素,实现pivot分割数组,最终使得左右指针相遇
nums[pivot], nums[j] = nums[j], nums[pivot] # 交换基准与左右指针相遇位置的元素,此次分区结束,新排序的数组一定是pivot元素大于左区,小于右区
quick(left, j-1) # 递归左半区
quick(j+1, right) # 递归右半区
return nums
return quick(0, length-1)
golang
// 6.quick
func quickSort(nums []int) []int {
length := len(nums)
var quick func(nums []int, left, right int) []int
quick = func(nums []int, left, right int) []int {
if left > right {return nil}
i, j, pivot := left, right, nums[left]
for i < j {
for i < j && nums[j] >= pivot {
j--
}
for i < j && nums[i] <= pivot {
i++
}
nums[i], nums[j] = nums[j], nums[i]
}
nums[i], nums[left] = nums[left], nums[i]
quick(nums, left, i-1)
quick(nums, i+1, right)
return nums
}
return quick(nums, 0, length-1)
}
7.计数排序
计数排序是典型的空间换时间算法,开辟额外数据空间存储用索引号记录数组的值和数组值个数
思路:
- 找出待排序的数组的最大值和最小值
- 创建数组存放各元素出现次数,限于[min, max]之间的数
- 统计数组值的个数
- 反向填充目标数组,填充的时候注意,nums[i] = j + min,j表示前面需要略过的数的个数,两个维度,一个是依次递增的数(j++),一个是重复的数的计数(j不变)
时空分析: 时间 O(n+k),数据量大时,花费时间与空间量大
稳定性:稳定
内排排序: 外排序
python
# 7.计数排序
def countSort(nums: [int]) -> [int]:
if not nums: return []
length = len(nums)
Min = min(nums)
Max = max(nums)
# 创建基于最值的有限数组并初始化
tempArr = [0] * (Max-Min+1)
# 实现计数, >0代表下标数出现次数, 如果0比较多,表示[min, max]之间的nums数组元素,某些是没有的,即空间换时间
for num in nums:
tempArr[num-Min] += 1
j = 0 # 初始化
for i in range(length):
while tempArr[j] == 0: # 等于0表示次数减完或者需要跳过,自然就需要j++
j += 1
nums[i] = j + Min # 替换排序的值
tempArr[j] -= 1 # 出现次数--
return nums
golang
// 7.count
func countSort(nums []int) []int {
if len(nums) == 0 {return []int{}}
length := len(nums)
min_ := func(arr []int) int {
minNum := math.MaxInt32
for _, val := range arr {
if val <= minNum {
minNum = val
}
}
return minNum
} (nums)
max_ := func(arr []int) int {
maxNum := math.MinInt32
for _, val := range arr {
if val >= maxNum {
maxNum = val
}
}
return maxNum
} (nums)
tempArr := make([]int, max_-min_+1)
for _, val := range nums {
tempArr[val-min_]++
}
j := 0
for i:=0;i<length;i++ {
for tempArr[j] == 0 {
j++
}
nums[i] = j + min_
tempArr[j]--
}
return nums
}
8.桶排序
桶排序是计数排序的升级版,原理是:输入数据服从均匀分布的,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的算法或是以递归方式继续使用桶排序,此文编码采用递归方式)
算法描述:
- 人为设置一个桶的BucketSize,作为每个桶放置多少个不同数值(意思就是BucketSize = 5,可以放5个不同数字比如[1, 2, 3,4,5]也可以放 100000个3,只是表示该桶能存几个不同的数值)
- 遍历待排序数据,并且把数据一个一个放到对应的桶里去
- 对每个不是桶进行排序,可以使用其他排序方法,也递归排序
- 不是空的桶里数据拼接起来
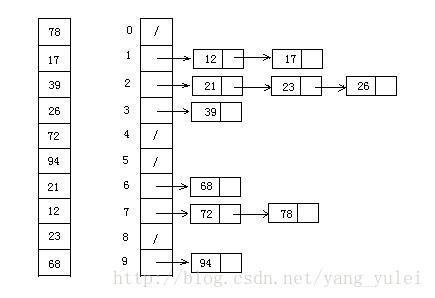
思路:
时空分析: 时间 O(n+k)
稳定性:稳定
内排排序: 外排序
python
# 8.桶排序
def bucketSort(nums: [int]) -> [int]:
def bucket_sort(nums: [int], bucketSize: int) -> [int]:
if len(nums) < 2:
return nums
min_ = min(nums)
max_ = max(nums)
# 需要桶的数量
bucketNum = (max_-min_) // bucketSize + 1
buckets = [[] for _ in range(bucketNum)]
for num in nums:
# 放入对应桶中
buckets[(num-min_) // bucketSize].append(num)
res = []
for bucket in buckets:
if not bucket: continue
if bucketSize == 1:
res.extend(bucket)
else:
# 全部放一个桶,说明容量大了
if bucketNum == 1:
bucketSize -= 1
res.extend(bucket_sort(bucket, bucketSize))
return res
bucketSize = 5
return bucket_sort(nums, bucketSize)
golang
// 8.bucket
func bucketSort(nums []int) []int {
var bucket_sort func(nums []int, bucketSize int) []int
bucket_sort = func(nums []int, bucketSize int) []int {
if len(nums) < 2 {
return nums
}
min_ := func(arr []int) int {
minNum := math.MaxInt32
for _, val := range arr {
if val <= minNum {
minNum = val
}
}
return minNum
} (nums)
max_ := func(arr []int) int {
maxNum := math.MinInt32
for _, val := range arr {
if val >= maxNum {
maxNum = val
}
}
return maxNum
} (nums)
buckets := make([][]int, bucketSize)
for j:=0;j<len(nums);j++ {
n := (nums[j]-min_) / ((max_-min_+1)/bucketSize)
buckets[n] = append(buckets[n], nums[j])
k := len(buckets[n]) - 2
for k>=0 && nums[j] < buckets[n][k] {
buckets[n][k+1] = buckets[n][k]
k--
}
buckets[n][k+1] = nums[j]
}
j := 0
for p, q := range buckets {
for t:=0;t<len(q);t++ {
nums[j] = buckets[p][t]
j++
}
}
return nums
}
var bucketSize int = 5
return bucket_sort(nums, bucketSize)
}
9.基数排序
思路:
基数排序是对数字每一位进行排序,从最低位开始排序
算法描述:
- 找到数组最大值,得最大位数;
- 从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(计数排序适用于小范围的特点)。
时空分析: 时间 O(n*k)
稳定性:稳定
内排排序: 外排序
python
# 9.基数排序
def radixSort(nums: [int]) -> [int]:
if not nums: return []
max_ = max(nums)
# 最大位数
maxDigit = len(str(max_))
bucketList = [[] for _ in range(10)]
# 从低位开始
div, mod = 1, 10
for i in range(maxDigit):
for num in nums:
bucketList[num % mod // div].append(num)
div *= 10
mod *= 10
index = 0
for j in range(10):
for item in bucketList[j]:
nums[index] = item
index += 1
bucketList[j] = []
return nums
golang
待完善
10.堆排序
思路:
堆排序是利用堆这个数据结构设计的排序算法。
算法描述:
- 建堆,从底向上调整堆,使得父亲节点比孩子节点值大,构成大顶堆;
- 交换堆顶和最后一个元素,重新调整堆。
时空分析: 时间 O(nlogn)
稳定性:不稳定
内排排序: 内排序
python
# 10.堆排序-不稳定-内排序-时间复杂度O(nlogn)
def heapSort(nums: [int]) -> [int]:
# 调整堆
# 迭代法
def adjustHeap(nums, startPos, endPos):
newItem = nums[startPos]
pos = startPos
childPos = pos*2 + 1
while childPos < endPos:
rightPos = childPos + 1
if rightPos < endPos and nums[rightPos] >= nums[childPos]:
childPos = rightPos
if newItem < nums[childPos]:
nums[pos] = nums[childPos]
pos = childPos
childPos = pos*2 + 1
else:
break
nums[pos] = newItem
# 递归法
def adjustHeap_(nums, startPos, endPos):
pos = startPos
childPos = pos*2 + 1
if childPos < endPos:
rightPos = childPos + 1
if rightPos < endPos and nums[rightPos] > nums[childPos]:
childPos = rightPos
if nums[childPos] > nums[pos]:
nums[pos], nums[childPos] = nums[childPos], nums[pos]
adjustHeap_(nums, pos, endPos)
length = len(nums)
# 1.建堆
for i in reversed(range(length//2)):
adjustHeap(nums, i, length)
# 2.调整堆
for i in range(length-1, -1, -1):
nums[0], nums[i] = nums[i], nums[0]
adjustHeap(nums, 0, i)
return nums
golang
// 10.heap
func heapSort(nums []int) []int {
end := len(nums) - 1
for i:=end/2;i>=0;i-- {
sink(nums, i, end)
}
for i:=end;i>=0;i-- {
nums[0], nums[i] = nums[i], nums[0]
end--
sink(nums, 0, end)
}
return nums
}
// 堆排-建堆
func sink(nums []int, root, end int) {
for {
child := root * 2 + 1
if child > end {
return
}
if child < end && nums[child] <= nums[child+1] {
child++
}
if nums[root] > nums[child] {
return
}
nums[root], nums[child] = nums[child], nums[root]
root = child
}
}