n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
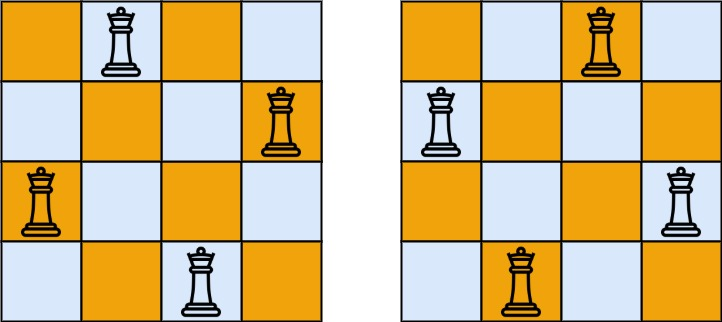
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
1 <= n <= 9
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/n-queens
参考:
python
# 0051.N皇后
class Solution:
def solveNQueens(self, n: int) -> [[str]]:
if not n:
return
board = [['.']*n for _ in range(n)]
res = []
def isVaild(board, row, col):
# 判断同列是否冲突
for i in range(len(board)):
if board[i][col] == 'Q':
return False
# 判断左上角是否冲突
i = row - 1
j = col - 1
while i >= 0 and j >= 0:
if board[i][j] == 'Q':
return False
i -= 1
j -= 1
# 判断右上角是否冲突
i = row - 1
j = col + 1
while i >= 0 and j < len(board):
if board[i][j] == 'Q':
return False
i -= 1
j += 1
return True
def backTrack(board, row, n):
# 如果走到最后一步,说明已经找到一个解
if row == n:
tmp_res = []
for tmp in board:
tmp_str = ''.join(tmp)
tmp_res.append(tmp_str)
res.append(tmp_res)
for col in range(n):
if not isVaild(board, row, col):
continue
board[row][col] = 'Q'
backTrack(board, row+1, n) # 同行不重复
board[row][col] = '.'
backTrack(board, 0, n)
return res
golang
package backTrack
import "strings"
var res [][]string
func isVaild(board [][]string, row, col int) (res bool) {
n := len(board)
// 检查行
for i:=0;i<row;i++ {
if board[i][col] == "Q" {
return false
}
}
// 检查列
for i:=0;i<n;i++ {
if board[row][i] == "Q" {
return false
}
}
// 检查左对角线
for i,j:=row,col;i>=0 && j >=0; i,j = i-1, j-1 {
if board[i][j] == "Q" {
return false
}
}
// 检查右对角线
for i,j:=row,col;i>=0 && j<n;i,j = i-1,j+1 {
if board[i][j] == "Q" {
return false
}
}
return true
}
func backTrackNQueens(board [][]string, row int) {
size := len(board)
if row == size {
temp := make([]string, size)
for i:=0;i<size;i++ {
temp[i] = strings.Join(board[i], "")
}
res = append(res, temp)
return
}
// 处理-递归-回溯
for col:=0;col < size; col++ {
if !isVaild(board, row, col) {
continue
}
board[row][col] = "Q"
backTrackNQueens(board, row+1)
board[row][col] = "."
}
}
func solveNQueens(n int) [][]string {
res = [][]string{}
board := make([][]string, n)
for i:=0;i<n;i++ {
board[i] = make([]string, n)
}
for i:=0;i<n;i++ {
for j:=0;j<n;j++ {
board[i][j] = "."
}
}
backTrackNQueens(board, 0)
return res
}