• 机器学习基础 | 相似度或距离的度量

    目录

    在机器学习的聚类或者分类任务中，需要度量样本间的距离或者相似度。

    本文总结常见距离(相似度)的计算方法。

    本文主要关注“数值数据”的相似度(距离)的度量，对于布尔数据、文本数据、图像数据的相似性度量，可以参考如下资料：

    Minkowski Distance

    给定样本集合(X)，(X)是m维实数向量空间(R^{m})中点的集合，其中:

    • (x_i,x_j in X)
    • (x_i = (x_{1i},x_{2i},...,x_{mi})^{T})
    • (x_j = (x_{1j},x_{2j},...,x_{mj})^{T})

    那么，(x_i)和(x_j)之间的闵可夫斯基距离(Minkowski Distance，简称闵氏距离) 定义为

    [d_{ij} = iggl(sum^{m}_{k=1}|x_{ki}- x_{kj}|^piggr)^{frac{1}{p}} ]

    这里(p ge 1).

    需要注意的是，Minkowski Distance对数据的量纲很敏感，比如样本中的某个维度单位表示为公里或米的时候，计算得到的距离差异是很大的，所以一般会对距离进行“标准化”以减小量纲带来的差异(当然，也可以在数据预处理的时候对各维度数据进行标准化或者归一化).

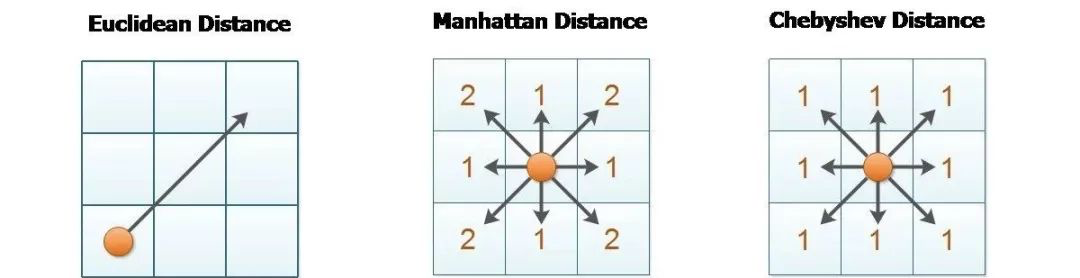
    当闵氏距离中p=1时，得到的距离为曼哈顿距离(Mahattan Distance)，也被称为City-Block Distance或者Texicab Distance。

    [d_{ij} = sum^{m}_{k=1}|x_{ki}- x_{kj}| ]

    对于曼哈顿距离的直观理解可参考下图，出租车要从城市的一个点到达另一个点，不能走直线(欧氏距离)，只能选择横来纵去地穿越一段段街道(如图中的小格子)。

    source

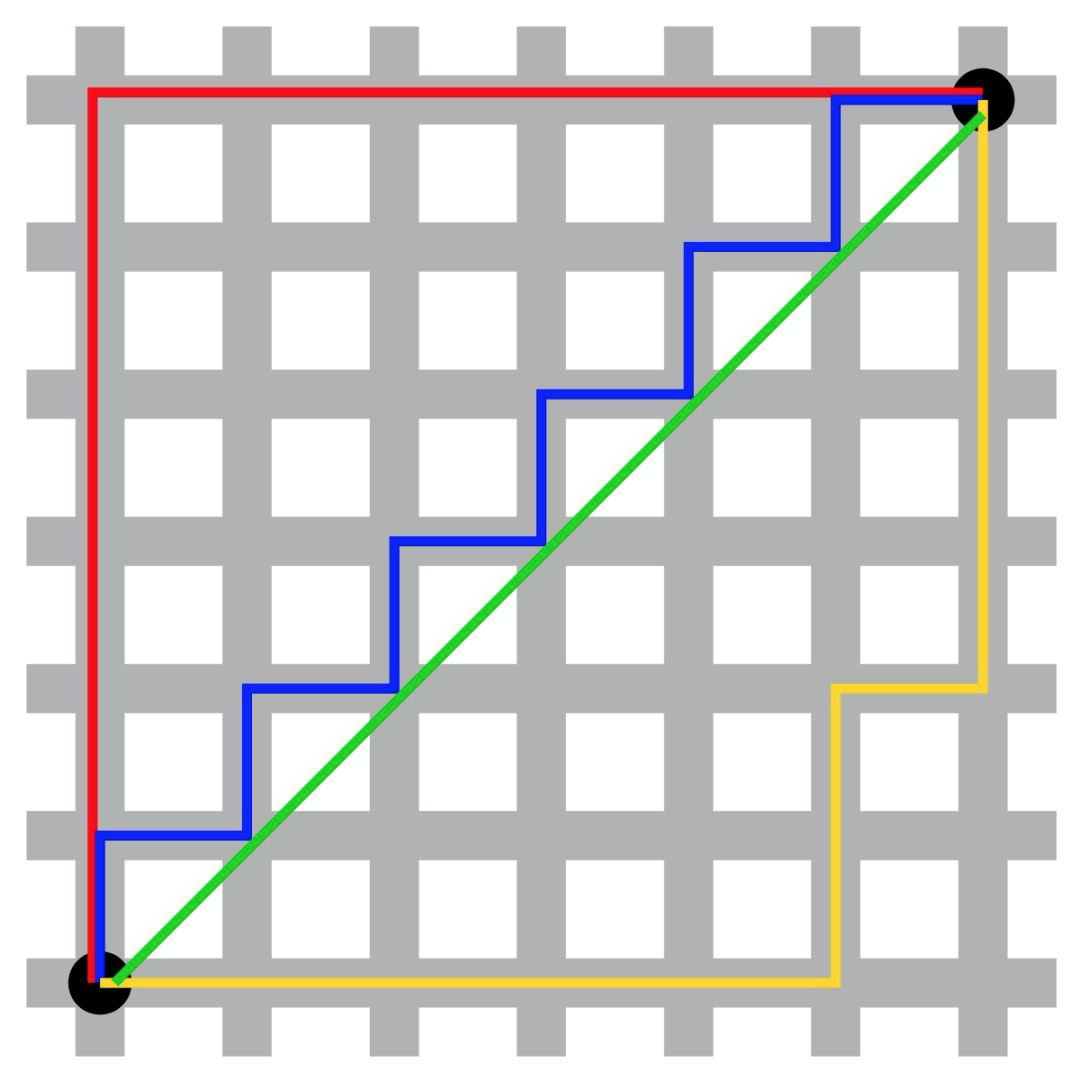
    由曼哈顿距离可以衍生出带权重的Canberra Distiance(Lance & Williams 1966)。

    [d_{ij} = sum^{m}_{k=1}frac{|x_{ki}- x_{kj}|}{|x_{ki}|+|x_{kj}|} ]

    当闵氏距离中p=2时，得到的距离是欧氏距离(Euclidian Distance) ，也就是通常意义上我们理解的空间中两点之间的直线距离(如上图中绿色的直线)。

    [d_{ij} = iggl(sum^{m}_{k=1}|x_{ki}- x_{kj}|^2iggr)^{frac{1}{2}} ]

    从欧氏距离又可以衍生出：

    • 平方欧氏距离(SquaredEuclideanDistance)

    [d_{ij} = sum^{m}_{k=1}|x_{ki}- x_{kj}|^2 ]

    • 归一化平方欧氏距离(Normalized Squared Euclidean Distance)

    [d_{ij} = frac{sum^m_{k=1}[(x_{ki}-overline{x_i})-(x_{kj}-overline{x_j})]^2}{2sum^m_{k=1}[(x_{ki}-overline{x_i})^2+(x_{kj}-overline{x_j})^2]} ]

    • 标准化欧氏距离(Standardized Euclidean distance)，相当于在各维度上进行标准化后在计算欧氏距离，即设标准化后得到的样本为(x'_i,x'_j)，第k个维度上的均值为(overline{x}_k)，方差为(s_k)，那么有

    [x'_{ki} = frac{x_{ki}-overline{x}_k}{s_k} ]

    [x'_{kj} = frac{x_{kj}-overline{x}_k}{s_k} ]

    由此可推导得到标准化后的欧氏距离为

    [egin{aligned} d(x'_i,x'_j) & = iggl(sum^m_{k=1}|x'_{ki}-x'_{kj}|^2iggr)^{frac{1}{2}} \ & = iggl(sum^m_{k=1}iggl|frac{x_{ki}-x_{kj}}{s_k}iggr|^2iggr)^{frac{1}{2}} \ & = iggl(sum^m_{k=1}frac{1}{s^2_k}igl|x_{ki}-x_{kj}igr|^2iggr)^{frac{1}{2}} \ end{aligned} ]

    如果把上式中(frac{1}{s^2_k})看做是权重系数，则可以得到加权欧氏距离(Weighted Euclidean distance) ，也就是在计算欧氏距离的时候可以为不同的维度指定不同的权重系数。

    当闵氏距离中p=+∞时，则为切比雪夫距离(Chebyshev Distance) ，也被称之为Chessboard Distance.

    [d_{ij} = underset{k}{max}|x_{ki}-x_{kj}| ]

    source

    Pearson Correlation Coefficient

    当用两列变量之间的共变性来衡量相似度的时候，可以使用皮尔森相关系数(Pearson Correlation Coefficient)。

    [egin{aligned} r_{ij} & = frac{Cov(x_i,x_j)}{delta_{x_i}delta_{x_j}} \ Cov(x_i,x_j) & = frac{1}{m} cdot sum^m_{k=1}(x_{ki}-overline{x}_i)(x_{kj}-overline{x}_j) \ delta_{x_i} & = sqrt{frac{sum^m_{k=1}(x_{ki}-overline{x}_i)^2}{m}} \ delta_{x_j} & = sqrt{frac{sum^m_{k=1}(x_{kj}-overline{x}_j)^2}{m}} \ end{aligned} ]

    基于上述4式，容易推导出如下表达式

    [r_{ij} = frac{sum^m_{k=1}(x_{ki}-overline{x}_i)(x_{kj}-overline{x}_j)}{igl[sum^m_{k=1}(x_{ki}-overline{x}_i)^2 sum^m_{k=1}(x_{kj}-overline{x}_j)^2igr]^{frac{1}{2}}} ]

    其中(r_{ij} in [-1,1]).

    Cosine Similarity

    夹角余弦(cosine)用来衡量两个向量在空间中方向的一致性(夹角的大小)。

    [egin{aligned} s_{ij} & = frac{x_i cdot x_j}{|x_i| cdot |x_j|}\ & = frac{sum^m_{k=1}x_{ki}x_{kj}}{igl[sum^m_{k=1}x^2_{ki} cdot sum^m_{k=1}x^2_{kj} igr]^{frac{1}{2}}} end{aligned} ]

    对比余弦距离和相关系数，可以发现相关系数是余弦距离在两个向量上的均值进行平移。

    Mahalanobis Distance

    给定样本集合(X,X=(x_{ij})_{m imes n})，其协方差矩阵为(S)(相对于样本集合而言).
    样本(x_i)：(x_i = (x_{1i},x_{2i},...,x_{mi})^T)
    样本(x_j)：(x_j = (x_{1j},x_{2j},...,x_{mj})^T)
    则样本(x_i)和样本(x_j)之间的马哈拉诺比斯距离(Mahalanobis Distance，简称马氏距离)定义为

    [d_{ij} = igl[(x_i-x_j)^TS^{-1}(x_i-x_j)igr]^{frac{1}{2}} ]

    从上述公式中可以看到，如果协方差矩阵(S)为单位矩阵，也就是样本数据中各分量相互独立(协方差矩阵中非主对角线的元素均为0)且各分量的方差为1时，那么马氏距离等价于欧氏距离。
    马氏距离实质上是一个点和一个数据分布的距离，而不是两个独立点之间的距离。
    除了分类(聚类)问题，马氏距离还可以用于离群点检测(Outlier Detection)。

    更多关于马氏距离的信息可以参考这篇文章
    关于协方差矩阵可参考这篇文章

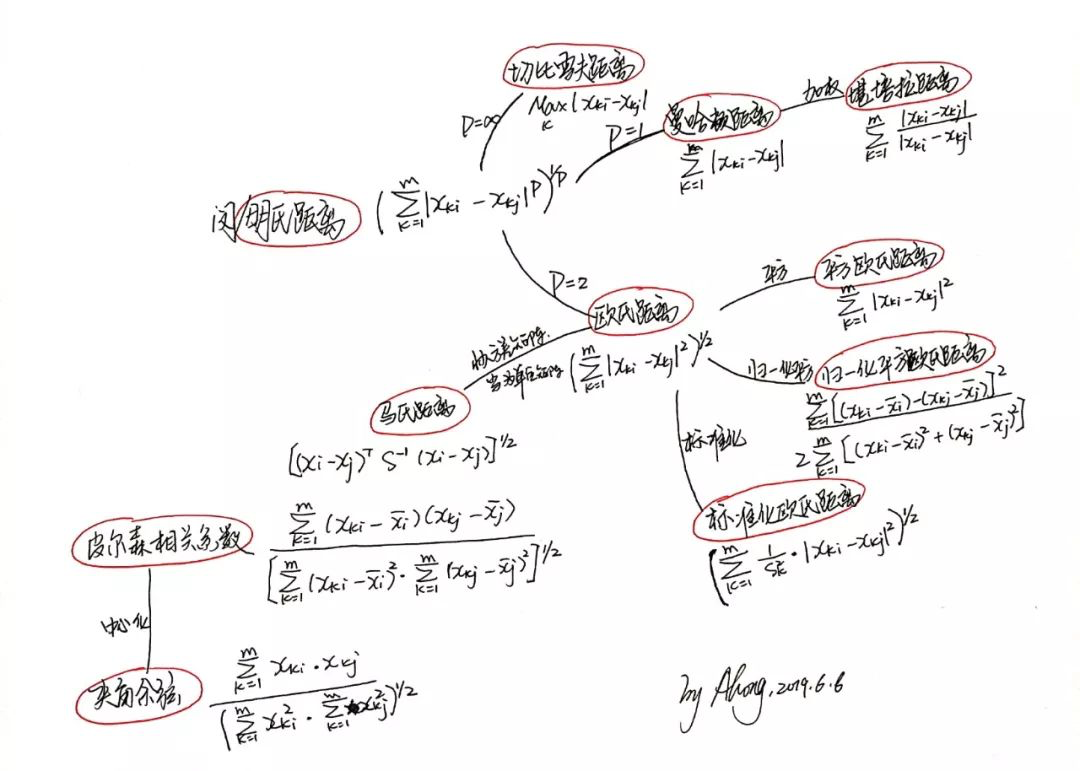
    以一张图总结本文主要内容：

    上述距离均可用scipy包中scipy.spatial.distance模块来计算。
    相应函数截图如下,更多可参考scipy文档

    参考资料

    本博客所有文章仅用于学习、研究和交流目的，欢迎非商业性质转载。

    转载请注明作者及出处
  • 相关阅读:
    eclipse如何正确部署tomcat7
    调用awk的三种方式
    jupyter的简单操作
    编程语言简介
    2019.9.6作业
    计算机的基本组成
    9.2作业
    CPP 栈 示例
    关于使用栈将一般运算式翻译为后缀表达式并实现三级运算的方法及实例（cpp版）
    深度遍历破解数独游戏
  • 原文地址：https://www.cnblogs.com/dataxon/p/12540117.html
Copyright © 2020-2023  润新知