pytorch入门2.x构建回归模型系列:
pytorch入门2.0构建回归模型初体验(数据生成)
pytorch入门2.1构建回归模型初体验(模型构建)
pytorch入门2.2构建回归模型初体验(开始训练)
经过上面两个部分,我们完成了数据生成、网络结构定义,下面我们终于可以小试牛刀,训练模型了!
首先,我们先定义一些训练时要用到的参数:
EPOCH = 1000 # 就是要把数据用几遍
LR = 0.1 # 优化器的学习率,类似爬山的时候应该迈多大的步子。
# BATCH_SIZE=50
其次,按照定义的模型类实例化一个网络:
if torch.cuda.is_available(): # 检查机器是否支持GPU计算,如果支持GPU计算,那么就用GPU啦,快!
model = LinearRegression().cuda() # 这里的这个.cuda操作就是把模型放到GPU上
else:
model = LinearRegression() # 如果不支持,那么用cpu也可以哦
# 定义损失函数,要有个函数让模型的输出知道他做的对、还是错,对到什么程度或者错到什么程度,这就是损失函数。
loss_fun = nn.MSELoss() # loss function
# 定义优化器,就是告诉模型,改如何优化内部的参数、还有该迈多大的步子(学习率LR)。
optimizer = torch.optim.SGD(model.parameters(), lr=LR) # opimizer
下面终于可以开始训练了,但是训练之前解释一下EPOCH,比如我们有300个样本,训练的时候我们不会把300个样本放到模型里面训练一遍,就停止了。即在模型中我们每个样本不会只用一次,而是会使用多次。这300个样本到底要用多少次呢,就是EPOCH的值的意义。
for epoch in range(EPOCH):
# 此处类似前面实例化模型是,我们把模型放到GPU上来跑道理是一样的。此处,我们要把变量放到GPU上,跑的快!如果不行, 那就放到CPU上吧。
# 其中x是输入数据,y是训练集的groundtruth。为什么要有y呢?因为我们要知道我们算的对不对,到底有多对(这里由损失函数控制)
if torch.cuda.is_available():
x = Variable(x_train).cuda()
y = Variable(y_train).cuda()
else:
x = Variable(x_train)
y = Variable(y_train)
# 我们把x丢进模型,得到输出y。哇,是不是好简单,这样我们就得到结果了呢?但是不要高兴的太早,我们只是把输入数据放到一个啥都不懂(参数没有训练)的模型中,得到的结果肯定不准啊。不准的结果怎么办,看下一步。
out = model(x)
# 拿到模型输出的结果,我们就要看看模型算的准不准,就是计算损失函数了。
loss = loss_fun(out,y)
# 好了好了,我已经知道模型算的准不准了,那么就该让模型自己去朝着好的方向优化了。模型,你已经是个大孩子了,应该会自己优化的。
optimizer.zero_grad() # 在优化之前,我们首先要清空优化器的梯度。因为每次循环都要靠这个优化器呢,不能翻旧账,就只算这次我们怎么优化。
loss.backward() # 优化开始,首先,我们要把算出来的误差、损失倒着传回去。(是你们这些模块给我算的这个值,现在这个值有错误,错了这么多,返回给你们,你们自己看看自己错哪了)
optimizer.step() # 按照优化器的方式,一步一步优化吧。
if (epoch+1)%100==0: # 中间每循环100次,偷偷看看结果咋样。
print('Epoch[{}/{}],loss:{:.6f}'.format(epoch+1,EPOCH,loss.data.item()))
上面我们训练了1000(EPOCH=1000)次,应该差不多了。是时候看看训练的咋样啦!其实我们已经知道训练的咋样了,就是上面输出的损失值,只不过是在训练集上的。
下面我们就要看看在测试集上表现咋样呢?
model.eval() # 开启模型的测试模式
# 拿到测试集中x的值,放到GPU上
if torch.cuda.is_available():
x = x_test.cuda()
#通过把x的值输入模型,得到预测结果
predict = model(x)
# 那预测结果的值取出来,因为预测结果是封装好的,现在h只要它的值。
predict = predict.cpu().data.numpy()
#画个图看看,到底拟合成啥样了?
plt.plot(x.cpu().numpy(),y_test.cpu().numpy(),'ro',label='original data')
plt.plot(sorted(x.cpu().numpy()),sorted(predict),label='fitting line')
plt.show()
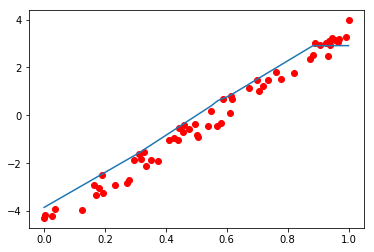
看看图,结果还凑合吧,要想结果更好需要进一步对模型的结构、超参数进行设置,我们之后在学。
到此为止,我们用pytorch就已经建立完,并且训练完一个线性回归模型了,我们可以回顾下,多看几遍,仔细回想一下这里面到底发生了什么。
完整的代码地址如下:github