问题1 :输入一个字符串,打印出该字符串中字符的所有排列。例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。
思路:这是个递归求解的问题。递归算法有四个特性:(1)必须有可达到的终止条件,否则程序将陷入死循环;(2)子问题在规模上比原问题小;(3)子问题可通过再次递归调用求解;(4)子问题的解应能组合成整个问题的解。
对于字符串的排列问题。如果能生成n - 1个元素的全排列,就能生成n个元素的全排列。对于只有1个元素的集合,可以直接生成全排列。全排列的递归终止条件很明确,只有1个元素时。下面这个图很清楚的给出了递归的过程。
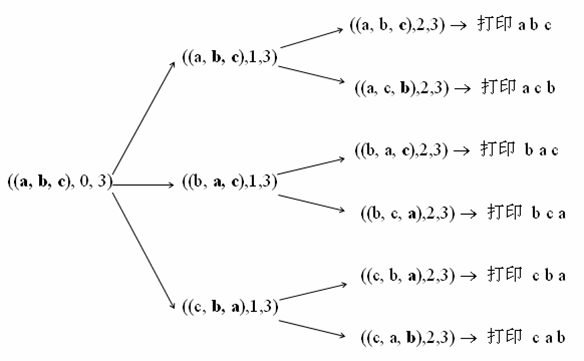
参考代码:解法1通过Permutation_Solution1(str, 0, n); 解法2通过调用Permutation_Solution2(str, str)来求解问题。
- //函数功能 : 求一个字符串某个区间内字符的全排列
- //函数参数 : pStr为字符串,begin和end表示区间
- //返回值 : 无
- void Permutation_Solution1(char *pStr, int begin, int end)
- {
- if(begin == end - 1) //只剩一个元素
- {
- for(int i = 0; i < end; i++) //打印
- cout<<pStr[i];
- cout<<endl;
- }
- else
- {
- for(int k = begin; k < end; k++)
- {
- swap(pStr[k], pStr[begin]); //交换两个字符
- Permutation_Solution1(pStr, begin + 1, end);
- swap(pStr[k],pStr[begin]); //恢复
- }
- }
- }
- //函数功能 : 求一个字符串某个区间内字符的全排列
- //函数参数 : pStr为字符串,pBegin为开始位置
- //返回值 : 无
- void Permutation_Solution2(char *pStr, char *pBegin)
- {
- if(*pBegin == '\0')
- {
- cout<<pStr<<endl;
- }
- else
- {
- char *pCh = pBegin;
- while(*pCh != '\0')
- {
- swap(*pBegin, *pCh);
- Permutation_Solution2(pStr, pBegin + 1);
- swap(*pBegin, *pCh);
- pCh++;
- }
- }
- }
- //提供的公共接口
- void Permutation(char *pStr)
- {
- Permutation_Solution1(pStr, 0, strlen(pStr));
- //Permutation_Solution2(pStr,pStr);
- }
问题2:输入一个字符串,输出该字符串中字符的所有组合。举个例子,如果输入abc,它的组合有a、b、c、ab、ac、bc、abc。
思路:同样是用递归求解。可以考虑求长度为n的字符串中m个字符的组合,设为C(n,m)。原问题的解即为C(n, 1), C(n, 2),...C(n, n)的总和。对于求C(n, m),从第一个字符开始扫描,每个字符有两种情况,要么被选中,要么不被选中,如果被选中,递归求解C(n-1, m-1)。如果未被选中,递归求解C(n-1, m)。不管哪种方式,n的值都会减少,递归的终止条件n=0或m=0。
- //函数功能 : 从一个字符串中选m个元素
- //函数参数 : pStr为字符串, m为选的元素个数, result为选中的
- //返回值 : 无
- void Combination_m(char *pStr, int m, vector<char> &result)
- {
- if(pStr == NULL || (*pStr == '\0'&& m != 0))
- return;
- if(m == 0) //递归终止条件
- {
- for(unsigned i = 0; i < result.size(); i++)
- cout<<result[i];
- cout<<endl;
- return;
- }
- //选择这个元素
- result.push_back(*pStr);
- Combination_m(pStr + 1, m - 1, result);
- result.pop_back();
- //不选择这个元素
- Combination_m(pStr + 1, m, result);
- }
- //函数功能 : 求一个字符串的组合
- //函数参数 : pStr为字符串
- //返回值 : 无
- void Combination(char *pStr)
- {
- if(pStr == NULL || *pStr == '\0')
- return;
- int number = strlen(pStr);
- for(int i = 1; i <= number; i++)
- {
- vector<char> result;
- Combination_m(pStr, i, result);
- }
- }
问题3:打靶问题。一个射击运动员打靶,靶一共有10环,连开10 枪打中90环的可能性有多少?
思路:这道题的思路与字符串的组合很像,用递归解决。一次射击有11种可能,命中1环至10环,或脱靶。
参考代码:
- //函数功能 : 求解number次打中sum环的种数
- //函数参数 : number为打靶次数,sum为需要命中的环数,result用来保存中间结果,total记录种数
- //返回值 : 无
- void ShootProblem_Solution1(int number, int sum, vector<int> &result, int *total)
- {
- if(sum < 0 || number * 10 < sum) //加number * 10 < sum非常重要,它可以减少大量的递归,类似剪枝操作
- return;
- if(number == 1) //最后一枪
- {
- if(sum <= 10) //如果剩余环数小于10,只要最后一枪打sum环就可以了
- {
- for(unsigned i = 0; i < result.size(); i++)
- cout<<result[i]<<' ';
- cout<<sum<<endl;
- (*total)++;
- return;
- }
- else
- return;
- }
- for(unsigned i = 0; i <= 10; i++) //命中0-10环
- {
- result.push_back(i);
- ShootProblem_Solution1(number-1, sum-i, result, total); //针对剩余环数递归求解
- result.pop_back();
- }
- }
- //提供的公共接口
- void ShootProblem(int number, int sum)
- {
- int total = 0;
- vector<int> result;
- ShootProblem_Solution1(number, sum, result, &total);
- cout<<"total nums = "<<total<<endl;
- }
FROM:http://blog.csdn.net/wuzhekai1985/article/details/6643127