manacher

洛谷板子题

（听过不止一遍，然而却一直没写过板子，于是今天模拟少了40分暴力分...）

一、字符串修饰

首先要修饰一下读进来的字符串。

为什么呢？

看两个字符串：

ABCCBA

ABCDCBA

显然这两字符串是回文的 然而两个串的对称中心的特性不同，第一个串，它的对称中心在两个C中间，然而第二个串，它的对称中心就是D。这样我们如果要记录回文串的对称中心，就显得复杂了。

为了解决这个问题，把两种情况统一起来，我们就在字母之间插入隔板，这样两个问题就统一了，因为所有的对称中心都会有个字符与之对应。像这样 ​ ~A|B|C|C|B|A|

（~方便判断字符边界，使当向两边扩展时，可以自动停止）

二、维护的数组

p[ i ] 维护以i为中心，最长回文串的半径长度 

rm 右边界最靠右的回文串右端点

mid 右边界最靠右的回文串对称中心

三、递推扫描

当我们扫描的点i的时候，它的对称点是 mid * 2 - i 

那么p[ i ] = min ( p[ mid * 2 - i ] ,rm - i);

这个式子怎么来的呢？为什么要和rm - i 取最小值呢？

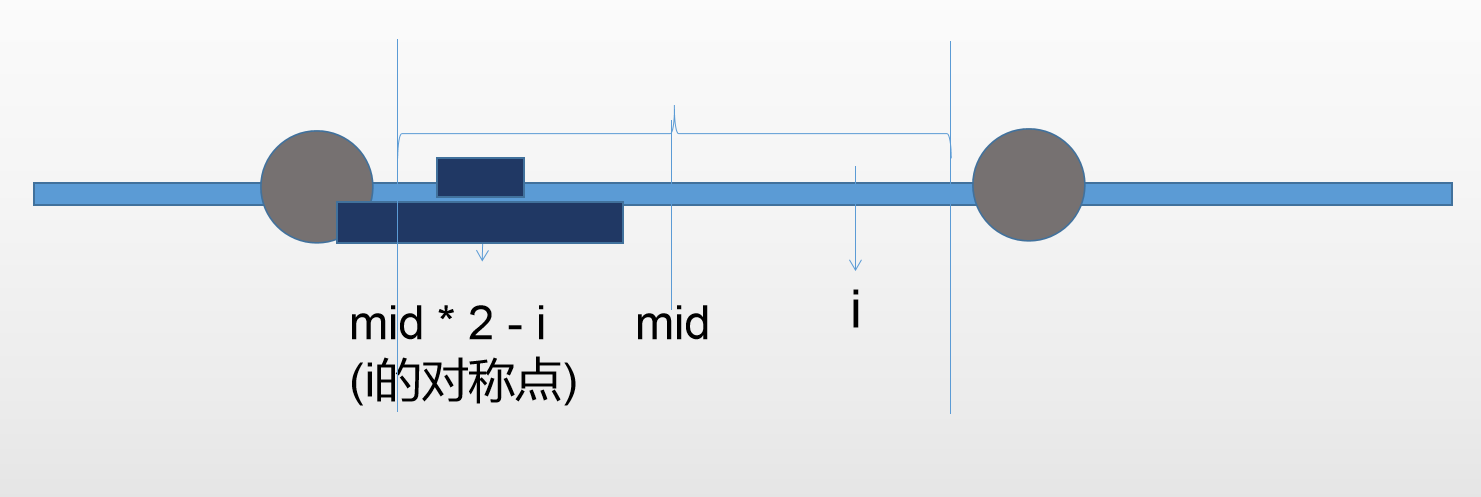
最细最长的淡蓝色长条是修饰过的字符串

两边两条垂直于淡蓝色长条的蓝线之间，是以mid为对称中心的最长回文串

那么两个灰色部分一定不对称（如果对称的话，就可以继续延伸了）

由于以i的对称点为中心的最长回文串可能是上面的蓝条也可能是下面了蓝条

如果是上面的蓝条：那么i处的回文串的长度就会=它的对称点的回文串的长度

（由于对称性）

如果是下面的蓝条：那么i出的回文串的长度一定!=它的对称点的回文串的长度（由于两块灰色部分的存在，使得它们不相同）

四、答案

通过不断地递推

最终答案就是：p[ max ] - 1;

五、码码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 11000005;
int cnt=1,rm,mid,ans;
char s[N<<1];
int p[N<<1];
inline void read()
{
    s[0] = '~';
    s[1] = '|';
    char ch = getchar();
    while(ch < 'a' || ch > 'z')
        ch = getchar();
    while(ch >= 'a' && ch <= 'z')
    {
        s[++cnt] = ch;
        s[++cnt] = '|';
        ch = getchar();
    }
    return;
}
int main()
{
    read();
    for(int i = 1;i <= cnt;i++)
    {
        if(i <= rm)
            p[i] = min(p[mid * 2 - i],rm - i);
        else
            p[i] = 1;
        while(s[i - p[i]] == s[i + p[i]])
            p[i]++;
        if(p[i]+i>rm)
        {
            rm = p[i] + i;
            mid = i;
        } 
        ans = max(ans,p[i]);
    }
    printf("%d",ans - 1);
    return 0;
}