主席树

又双叕是一个被我咕了很久的知识）

（我不爱数据结构）

板子题

一、主席树

又叫可持久化线段树

支持点修改和区间询问

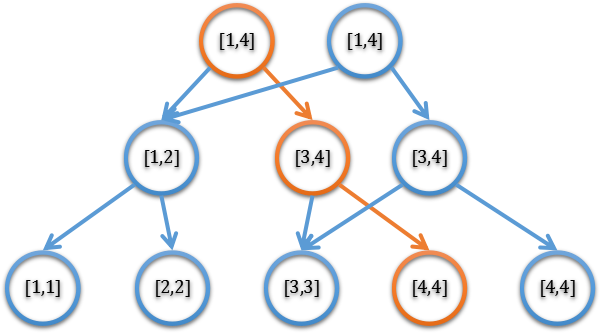
图中橙色节点为历史节点，其右边多出来的节点是新节点

二、数据结构

主席树的点修改：

不同于普通线段树，主席树的左右儿子节点编号并能够通过计算得到，所以应该记录下来

主席树的询问：

类似于线段树

三、复杂度

修改O(logn)

询问O(logn)

四、板子题

sum[ ]数组：sum[ x ]表示在某个区间内，x的个数

b[ ]数组：储存的是原序列a[ ]数组离散化后的序列

1.首先复制原数组，排序好，去掉多余的数，即将数据离散化。用unique去重

2.以离散化数组为基础，建一个全0的线段树，称作基础主席树

3.对于原数据中每一个[ 1 ，i ]区间统计，有序的插入新节点

4.对于查询[ 1 , r ]中第k小值的操作，找到[ 1 , r ] 对应的根节点，按照线段树的方法操作即可

注意：

修改点p开的是全局变量

数组别开的太小

注意函数的类型

#include<cstdio>
#include<algorithm>
using namespace std;

inline int read()
{
    int sum = 0,p = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
            p = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        (sum *= 10) += ch - '0';
        ch = getchar();
    }
    return sum * p;
}

const int maxn = 2e5 + 10; 
int n,m,cnt,p;
int a[maxn],b[maxn],sum[maxn<<5],rt[maxn],lc[maxn<<5],rc[maxn<<5];

void build(int & t,int l,int r)
{
    t = ++cnt;
    if(l == r)
        return;
    int mid = (l + r) >> 1;
    build(lc[t],l,mid);
    build(rc[t],mid + 1,r);
}

int modify(int o,int l,int r)
{
    int oo = ++cnt;
    lc[oo] = lc[o];
    rc[oo] = rc[o];
    sum[oo] = sum[o] + 1;
    if(l == r)
        return oo;
    int mid = (l + r) >> 1;
    if(p <= mid)
        lc[oo] = modify(lc[oo],l,mid);
    else
        rc[oo] = modify(rc[oo],mid + 1,r);
    return oo;
}

int query(int u,int v,int l,int r,int k)
{
    int ans;
    int mid = (l + r) >> 1;
    int x = sum[lc[v]] - sum[lc[u]];
    if(l == r)
        return l;
    if(x >= k)
        ans = query(lc[u],lc[v],l,mid,k);
    else
        ans = query(rc[u],rc[v],mid + 1,r,k - x);
    return ans;
}

int main()
{
    int l,r,k,q,ans;
    n = read(),m = read();
    for(int i = 1;i <= n;i++)
    {
        a[i] = read();
        b[i] = a[i];
    }
    sort(b + 1,b + n + 1);
    q = unique(b + 1,b + n + 1) - b - 1;
    build(rt[0],1,q);
    for(int i = 1;i <= n;i++)
    {
        p = lower_bound(b + 1,b + q + 1,a[i]) - b;
        rt[i] = modify(rt[i - 1],1,q);
    }
    while(m--)
    {
        l = read(),r = read(),k = read();
        ans = query(rt[l - 1],rt[r],1,q,k);
        printf("%d
",b[ans]);
    }
    return 0;
}