前置知识:
关于图的几个概念定义:
- 连通图:在无向图中,若任意两个顶点vi与vj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vi与vj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
一、定义
(看板子题就好)
给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
二、有两种算法
kruskal 和 prim
两者区别:Prim在稠密图中比Kruskal优,在稀疏图中比Kruskal劣。
Prim是以更新过的节点的连边找最小值,Kruskal是直接将边排序。
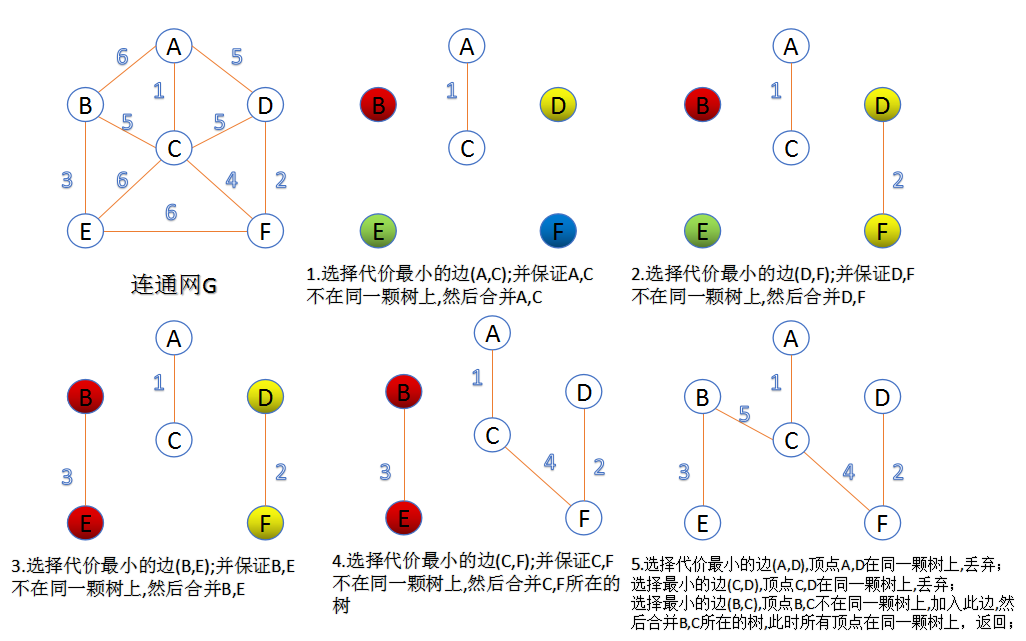
kruskal
此算法又可称为“加边法”
初始最小生成树边数为0
每迭代一次就选择一起满足条件的最小代价边,加入到最小生成树的边集合中
1.把图中的所有边按代价从小到大排序
2.把图中的n个顶点看成独立的n棵树
3.按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
#include<cstdio> #include<algorithm> #include<iostream> using namespace std; inline int read() { int sum = 0,p = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') p = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { (sum *= 10)+= ch - '0'; ch = getchar(); } return sum * p; } const int maxm = 200005,maxn = 5005; struct Edge { int from,to,wei; }edge[maxm]; int fa[maxn],n,m,ans,u,v,cnt; inline bool cmp(Edge a,Edge b) { return a.wei < b.wei; } int find(int o) { if(o == fa[o]) return o; else return fa[o] = find(fa[o]); } inline void kruskal() { sort(edge+1,edge+m+1,cmp); for(int i = 1;i <= m;i++) { u = find(edge[i].from); v = find(edge[i].to); if(u == v) continue; ans += edge[i].wei; fa[v] = u; if(++cnt == n - 1) break; } } int main() { n = read(),m = read(); for(int i = 1;i <= n;i++) fa[i] = i; for(int i = 1;i <= m;i++) { edge[i].from = read(); edge[i].to = read(); edge[i].wei = read(); } kruskal(); printf("%d",ans); return 0; }
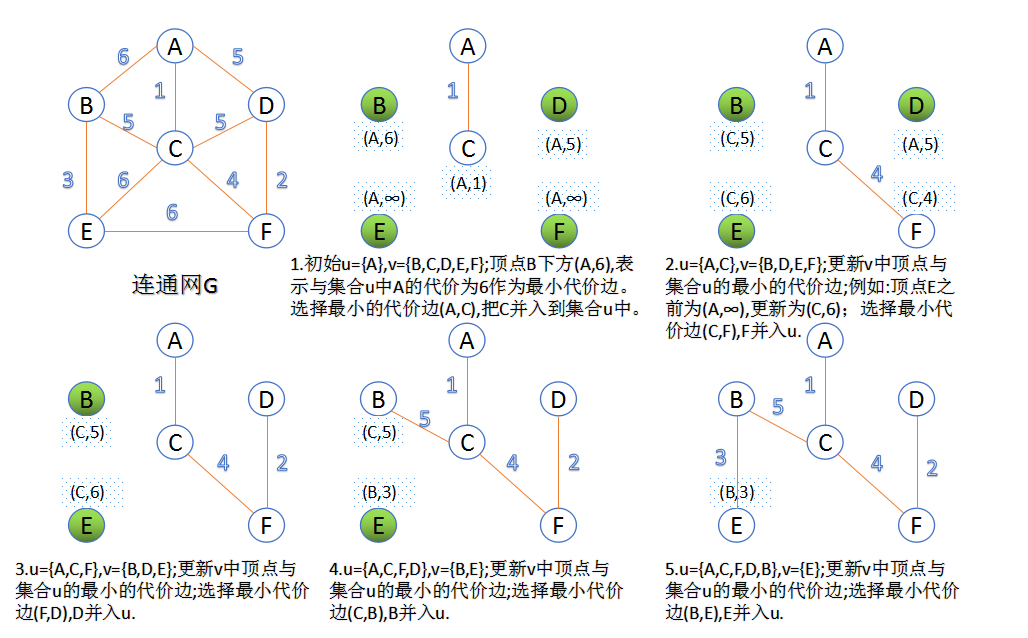
Prim
此算法也可以成为“加点法”
每次迭代选择代价最小的边对应的点加入到最小生成树中
算法从某一个顶点s开始逐渐长大覆盖整个连通网的所有顶点
1.图的所有顶点集合为v;初始令集合u={s},v=V-u;
2.在两个集合u,v能组成的边中,选择我一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中
3.重复上述步骤,知道最小生成树有n-1条边或者n个顶点为止
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
inline int read()
{
int sum = 0,p = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-')
p = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
(sum *= 10)+= ch - '0';
ch = getchar();
}
return sum * p;
}
const int maxn = 5005,maxm = 200005,inf = 123456789;
struct edge
{
int v,w,next;
}e[maxm<<1];
int head[maxn],dis[maxn],cnt,n,m,tot,now = 1,ans;
bool vis[maxn];
inline void add(int u,int v,int w)
{
e[++cnt].v = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt;
}
int prim()
{
for(int i = 2;i <= n;i++)
dis[i] = inf;
for(int i = head[1];i;i = e[i].next)
dis[e[i].v] = min(dis[e[i].v],e[i].w);
while(++tot<n)
{
int minn = inf;
vis[now] = true;
for(int i = 1;i <= n;i++)
if(!vis[i] && minn > dis[i])
{
minn = dis[i];
now = i;
}
ans += minn;
for(int i = head[now];i;i = e[i].next)
{
int v = e[i].v;
if(dis[v] > e[i].w && !vis[v])
dis[v] = e[i].w;
}
}
return ans;
}
int main()
{
n = read(),m = read();
int u,v,w;
for(int i = 1;i <= m;i++)
{
u = read(),v = read(),w = read();
add(u,v,w);
add(v,u,w);
}
printf("%d",prim());
return 0;
}