可以说这道也是一个板子题
由于题中是三个人需经过的路径最短
就会有一点点不太一样
那么
就两两求LCA
这样之后就会出现两种状况
一、所得到的三个LCA是相等的
那毫无疑问真正的LCA的值就是这个值
二、若不是第二种情况
那必然会出现
有且仅有一个LCA的值与令两个LCA的值不同
第二种情况正确性(不严格的)证明:
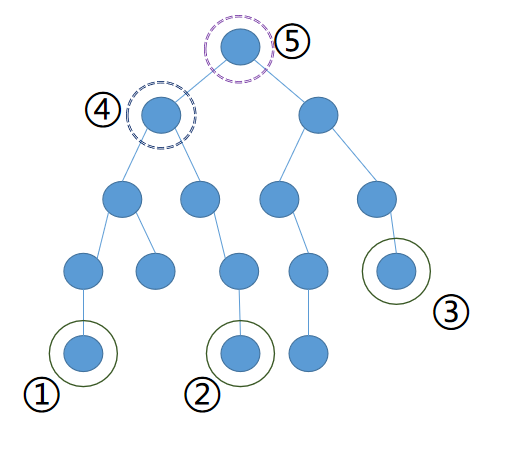
显然1和2的LCA是4
2和3的LCA是5
1和3的LCA也是5
既然2和3的LCA(5)的深度4大
那么也可把2和3的LCA看作是4和3的LCA
那么1和3的LCA也是5了
所以必定会有两个LCA是相同的
而且相同的那个一定是最高的
(因为 4和3的LCA是5 = 1和3的LCA是5 同时2 和3的LCA是5)
所以
找到了两个相同的
真正的LCA就是另一个
因为让3从5走到4
显然要比让1和2一起4走到5
同样都是要走4和5之间的相同的路径
只是方向不同而已
让1和2两个人一起走显然要比只要3走到长
所以真正的LCA是(与另外两个相同的LCA)不同的那个LCA,而不是相同的LCA了
然而当我信心满满写完的时候
我有sd了

需要减掉(即重复加到结果中的)被我简简单单的认为只是真正的LCA的深度*3
但是显然不是的啊
那这把是不是好了捏?
然而我输出的数不对啊
这可怎么回事??
我方了
(在各种瞎调试之下)
我把每一个处理fa[ ][ ]数组的循环次数从20加到的25
奇迹般地好了
(这是为什么,明明样例数据很小的啊,怎么会影响到的呢??)
跪求大佬们指点
这把终于过样例了
于是我开开心心的去提交了
结果re了
(又一脸懵)
于是我发现我sd的fa[ ][ ]数组忘再开大一点了
而且
由于是起初是无向图
所以
需要正反都要加边
但是我的数组只是一次加边的大小
既然就gg了
唉
什么时候可以不犯这种低级错误啊qwq...
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 500005;
int hed[maxn * 2],nxt[maxn * 2],to[maxn * 2],dep[maxn * 2];
bool vis[maxn];
int fa[maxn][30];
int n,m,cnt,rot;
inline int read()
{
int sum = 0,p = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-')
p = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
(sum *= 10)+= ch - '0';
ch = getchar();
}
return sum * p;
}
void add(int x,int y)
{
nxt[++cnt] = hed[x];
to[cnt] = y;
hed[x] = cnt;
}
void dfs(int o,int k)
{
dep[o] = dep[k] + 1;
for(int i = 0;i<= 25;i++)
fa[o][i+1] = fa[fa[o][i]][i];
for(int i = hed[o];i;i = nxt[i])
{
if(to[i] == k)
continue;
fa[to[i]][0] = o;
dfs(to[i],o);
}
}
int lca(int x,int y)
{
if(dep[x] < dep[y])
swap(x,y);
for(int i = 25;i >= 0;i--)
{
if(dep[fa[x][i]] >= dep[y])
x = fa[x][i];
if(x == y)
return x;
}
for(int i = 25;i >= 0;i--)
{
if(fa[x][i] != fa[y][i])
{
x = fa[x][i];
y = fa[y][i];
}
}
return fa[x][0];
}
int main()
{
n = read(),m = read();
for(int i = 1;i < n;i++)
{
int a = read(),b = read();
add(a,b);
add(b,a);
vis[b] = 1;
}
for(int i = 1;i <= n;i++)
{
if(!vis[i])
{
rot = i;
break;
}
}
dep[rot] = 1;
dfs(rot,0);
for(int i = 1;i <= m;i++)
{
int a = read(),b = read(),c = read();
int o = lca(a,b);
int p = lca(c,b);
int q = lca(a,c);
int u;
if(o == p)
u = q;
else
if(o == q)
u = p;
else
u = o;
printf("%d %d
",u,dep[a] + dep[b] + dep[c] - dep[o] - dep[p] - dep[q]);
}
return 0;
}