经典引例:
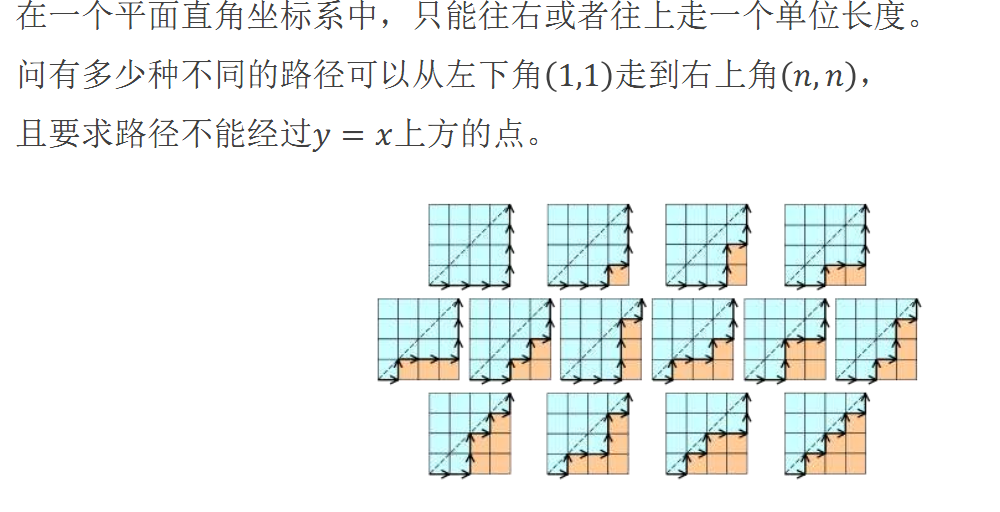
卡特兰数满足以下性质:
令h(0)=1,h(1)=1,catalan数满足递推式。
h(n)= h(0) * h(n - 1) + h(1) * h(n-2) + ... + h(n-1)h(0) (n>=2)
也就是说,如果能把公式化成上面这种形式的数,就是卡特兰数。

于是,有了引例的我们就可以,把类似的数学问题转化成图形来辅助思考,
或者
用能否转化成类似图形来判断是否是Catalan数
不同形式的Catalan数
1.引例。
2.左括号,右括号(有多少种不同的长度为n的合法序号序列)
3.进栈出栈(求有多少种操作序列)
4.二叉树(多少种不同的n各节点的二叉树)
5.多边形进行三角剖分的方案数