IoU算法可用与评估两个多维度数据的相似度,举一个实际应用,做CV,目标检测,我们需要评估模型的识别准确率,不同于二元类问题,普通的评估算法不合适,于是用到了这个算法,这个算法简单易懂,评估效果也不错。
这里主要讨论如何计算并评估两个矩形相交程度。有空再训练一个目标检测器,来试试水。。
第一种对于数据形状是这样的 $ (x_{top-left}, y_{top-left}, w, h) $,意思是:给出了起始坐标,矩形沿着 $ w, h $ 扩展开。
算法实现:
double IoU(int*a, int*b)
{
int overlap_w = min(a[0] + a[2], b[0] + b[2]) - max(a[0], b[0]);
int overlap_h = min(a[1] + a[3], b[1] + b[3]) - max(a[1], b[1]);
int overlap_s = overlap_w*overlap_h;
return overlap_s / double(a[2]*a[3] + b[2]*b[3] - overlap_s);
}
第二种数据形状是这样的 $ (x_{top-left}, y_{top-left}, x_{right-down}, y_{right-down}) $,意思是:给出了起始坐标和终点坐标,如图:
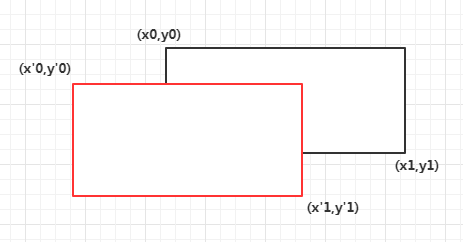
算法实现:
double IoU_2(int*a, int*b)
{
int overlap_w = min(a[2], b[2]) - max(a[0], b[0]);
int overlap_h = min(a[3], b[3]) - max(a[1], b[1]);
int overlap_s = overlap_w*overlap_h;
return overlap_s / double((a[2] - a[0])*(a[3] - a[1]) + (b[2] - b[0])*(b[3] - b[1]) - overlap_s);
}
用这几组数据测试一下:
1: [39, 63, 203, 112], [54, 66, 198, 114] 2: [49, 75, 203, 125], [42, 78, 186, 126] 3: [31, 69, 201, 125], [18, 63, 235, 135] 4: [50, 72, 197, 121], [54, 72, 198, 120] 5: [35, 51, 196, 110], [36, 60, 180, 108]
output:
0.825758 0.795771 ===================== 0.809624 0.787838 ===================== 0.791962 0.609319 ===================== 0.947743 0.946628 ===================== 0.79667 0.727656 =====================
参考:
1.https://www.pyimagesearch.com/2016/11/07/intersection-over-union-iou-for-object-detection/
2.https://en.wikipedia.org/wiki/Jaccard_index