从随机过程到马尔科夫链蒙特卡洛方法

 1. Introduction

第一次接触到 Markov Chain Monte Carlo (MCMC) 是在 theano 的 deep learning tutorial 里面讲解到的 RBM 用到了 Gibbs sampling，当时因为要赶着做项目，虽然一头雾水，但是也没没有时间仔细看。趁目前比较清闲，把 machine learning 里面的 sampling methods 理一理，发现内容还真不少，有些知识本人也是一知半解，所以这篇博客不可能面面俱到详细讲解所有的 sampling methods，而是着重讲一下这个号称二十世纪 top 10 之一的算法—— Markov chain Monte Carlo。在介绍 MCMC 之前，我们首先了解一下 MCMC 的 Motivation 和在它之前用到的方法。本人也是初学者，错误在所难免，欢迎一起交流。

这篇博客从零开始，应该都可以看懂，主要内容包括：

1. 随机采样
2. 拒绝采样
3. 重要性采样
4. Metropolis-Hastings Algorithm
5. Gibbs Sampling

2. Sampling

我们知道，计算机本身是无法产生真正的随机数的，但是可以根据一定的算法产生伪随机数（pseudo-random numbers)。最古老最简单的莫过于 Linear congruential generator：

式子中的 a 和 c 是一些数学知识推导出的合适的常数。但是我们看到，这种算法产生的下一个随机数完全依赖现在的随机数的大小，而且当你的随机数序列足够大的时候，随机数将出现重复子序列的情况。当然，理论发展到今天，有很多更加先进的随机数产生算法出现，比如 python 数值运算库 numpy 用的是 Mersenne Twister 等。但是不管算法如何发展，这些都不是本质上的随机数，用冯诺依曼的一句话说就是：

Anyone who considers arithmetic methods of producing random digits is, of course, in a state of sin.

要检查一个序列是否是真正的随机序列，可以计算这个序列的 entropy 或者用压缩算法计算该序列的冗余。

OK，根据上面的算法现在我们有了均匀分布的随机数，但是如何产生满足其他分布（比如高斯分布）下的随机数呢？一种可选的简单的方法是 Inverse transform sampling，有时候也叫Smirnov transform。拿高斯分布举例子，它的原理是利用高斯分布的累积分布函数（CDF，cumulative distribution function）来处理，过程如下图：

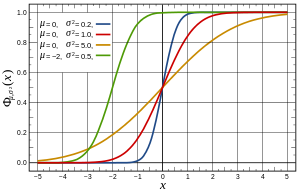
假如在 y 轴上产生（0,1）之间的均匀分布的随机数，水平向右投影到高斯累计分布函数上，然后垂直向下投影到 x 轴，得到的就是高斯分布。可见高斯分布的随机数实际就是均匀分布随机数在高斯分布的 CDF 函数下的逆映射。当然，在实际操作中，更有效的计算方法有 Box–Muller_transform (an efficient polar form)，Ziggurat algorithm 等，这些方法 tricky and faster，没有深入了解，这里也不多说了。

3. Motivation

MCMC 可解决高维空间里的积分和优化问题：

• 上面一个例子简单讲了利用高斯分布的 CDF 可以产生高斯随机数，但是有时候我们遇到一些分布的 CDF 计算不出来（无法用公式表示），随机数如何产生？

• 遇到某些无法直接求积分的函数，如 e^{x^2}，在计算机里面如何求积分？

• 如何对一个分布进行高效快速的模拟，以便于抽样？

• 如何在可行域很大(or large number of possible configurations)时有效找到最优解——RBM 优化目标函数中的问题。

• 如何在众多模型中快速找到更好的模型——MDL, BIC, AIC 模型选择问题。

3.1 The Monte Carlo principle

实际上，Monte Carlo 抽样基于这样的思想：假设玩一局牌的赢的概率只取决于你抽到的牌，如果用穷举的方法则有 52! 种情况，计算复杂度太大。而现实中的做法是先玩几局试试，统计赢的概率，如果你不太确信这个概率，你可以尽可能多玩几局，当你玩的次数很大的时候，得到的概率就非常接近真实概率了。

上述方法可以估算随机事件的概率，而用 Monte Carlo 抽样计算随即变量的期望值是接下来内容的重点：X 表示随即变量，服从概率分布 p(x), 那么要计算 f(x) 的期望，只需要我们不停从 p(x) 中抽样

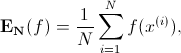
当抽样次数足够的时候，就非常接近真实值了：

Monte Carlo 抽样的方法还有一个重要的好处是：估计值的精度与 x 的维度无关（虽然维度越高，但是每次抽样获得的信息也越多），而是与抽样次数有关。在实际问题里面抽样二十次左右就能达到比较好的精度。

但是，当我们实际动手的时候，就会发现一个问题——如何从分布 p(x) 中抽取随机样本。之前我们说过，计算可以产生均匀分布的伪随机数。显然，第二小节产生高斯随机数的抽样方法只对少数特定的问题管用，对于一般情况呢？

3.2 Rejection Sampling

Reject Sampling 实际采用的是一种迂回( proposal distribution q(x) )的策略。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可抽样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，达到接近 p(x) 分布的目的：

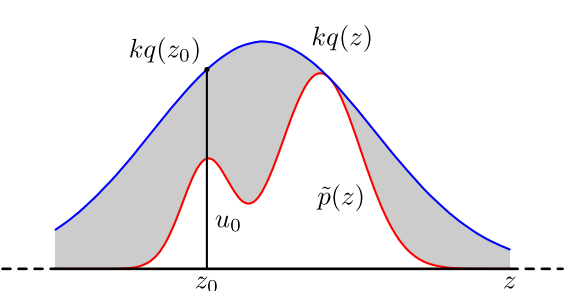
具体操作如下，设定一个方便抽样的函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。（参考上图）

• x 轴方向：从 q(x) 分布抽样得到 a。(如果是高斯，就用之前说过的 tricky and faster 的算法更快）
• y 轴方向：从均匀分布（0, kq(a)) 中抽样得到 u。
• 如果刚好落到灰色区域： u > p(a), 拒绝， 否则接受这次抽样
• 重复以上过程

用均匀分布拒绝抽样来近似两个高斯混合分布的代码如下：

rejectionsampling.py

# -*- coding=utf8 -*-

# Code from Chapter 14 of Machine Learning: An Algorithmic Perspective
# The basic rejection sampling algorithm

from pylab import *
from numpy import *

def qsample():
    return random.rand()*4.

def p(x):
    return 0.3*exp(-(x-0.3)**2) + 0.7* exp(-(x-2.)**2/0.3) 

def rejection(nsamples):
    
    M = 0.72#0.8
    samples = zeros(nsamples,dtype=float)
    count = 0
    for i in range(nsamples):
        accept = False
        while not accept:
            x = qsample()
            u = random.rand()*M
            if u<p(x):
                accept = True
                samples[i] = x
            else: 
                count += 1
    print count   
    return samples

x = arange(0,4,0.01)
x2 = arange(-0.5,4.5,0.1)
realdata = 0.3*exp(-(x-0.3)**2) + 0.7* exp(-(x-2.)**2/0.3) 
box = ones(len(x2))*0.75#0.8
box[:5] = 0
box[-5:] = 0
plot(x,realdata,'k',lw=6)
plot(x2,box,'k--',lw=6)

import time
t0=time.time()
samples = rejection(10000)
t1=time.time()
print "Time ",t1-t0

hist(samples,15,normed=1,fc='k')
xlabel('x',fontsize=24)
ylabel('p(x)',fontsize=24)
axis([-0.5,4.5,0,1])
show()

在高维的情况下，Rejection Sampling 会出现两个问题，第一是合适的 q 分布比较难以找到，第二是很难确定一个合理的 k 值。这两个问题会导致拒绝率很高，无用计算增加。

3.3 Importance Sampling

Importance Sampling 也是借助了容易抽样的分布 q (proposal distribution)来解决这个问题，直接从公式出发：

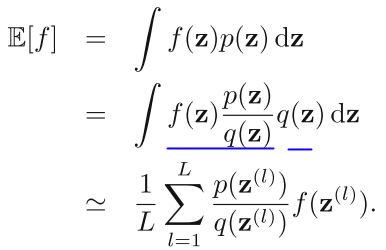
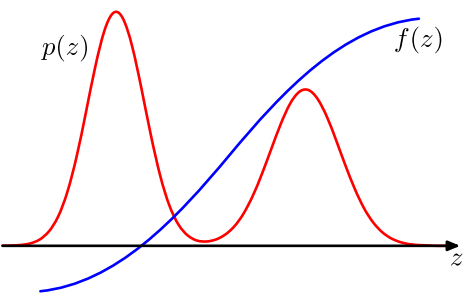
其中，p(z) / q(z) 可以看做 importance weight。我们来考察一下上面的式子，p 和 f 是确定的，我们要确定的是 q。要确定一个什么样的分布才会让采样的效果比较好呢？直观的感觉是，样本的方差越小期望收敛速率越快。比如一次采样是 0, 一次采样是 1000, 平均值是 500,这样采样效果很差，如果一次采样是 499, 一次采样是 501, 你说期望是 500,可信度还比较高。在上式中，我们目标是 p×f/q 方差越小越好，所以 |p×f| 大的地方，proposal distribution q(z) 也应该大。举个稍微极端的例子：

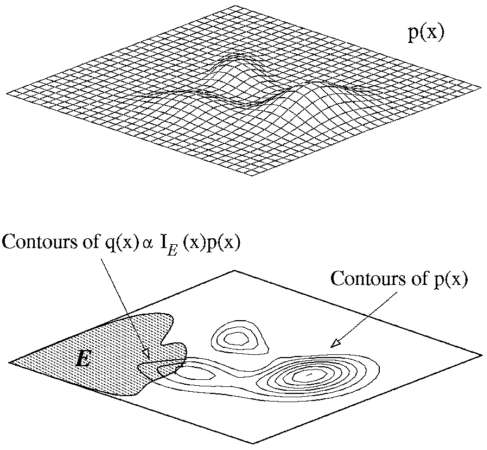
第一个图表示 p 分布， 第二个图的阴影区域 f = 1，非阴影区域 f = 0, 那么一个良好的 q 分布应该在左边箭头所指的区域有很高的分布概率，因为在其他区域的采样计算实际上都是无效的。这表明 Importance Sampling 有可能比用原来的 p 分布抽样更加有效。

但是可惜的是，在高维空间里找到一个这样合适的 q 非常难。即使有 Adaptive importance sampling 和 Sampling-Importance-Resampling(SIR) 的出现，要找到一个同时满足 easy to sample 并且 good approximations 的 proposal distribution, it is often impossible！

 

4. MCMC Algorithm

上面说了这么多采样方法，其实最终要突出的就是 MCMC 的过人之处。MCMC 的绝妙之处在于：通过稳态的 Markov Chain 进行转移计算，等效于从 P(x) 分布采样。但是在了解 MCMC 具体算法之前，我们还要熟悉 Markov Chain 是怎么一回事。

4.1 Markov Chain

Markov Chain 体现的是状态空间的转换关系，下一个状态只决定与当前的状态(可以联想网页爬虫原理，根据当前页面的超链接访问下一个网页)。如下图：

这个状态图的转换关系可以用一个转换矩阵 T 来表示：

举一个例子，如果当前状态为 u(x) = (0.5, 0.2, 0.3), 那么下一个矩阵的状态就是 u(x)T = (0.18, 0.64, 0.18), 依照这个转换矩阵一直转换下去，最后的系统就趋近于一个稳定状态 (0.22, 0.41, 0.37) (此处只保留了两位有效数字)。而事实证明无论你从那个点出发，经过很长的 Markov Chain 之后都会汇集到这一点。

考虑一般的情况，满足什么条件下经过很长的 Markov Chain 迭代后系统分布会趋近一个稳定分布，即最后的 u(x) 等效于从目标分布 p(x) 采样。大概的条件如下（自己随便总结的，可能有遗漏和错误）：

1. Irreducibility. 即图是联通的，T 矩阵不能被切豆腐一样划分成小方块，举个例子，比如爬虫爬不到内部局域网的网页
2. Aperiodicity. 即图中遍历不会陷入到一个死圈里，有些网站为了防机器人，会专门设置这种陷阱
3. Detailed Balance，这是保证系统有稳态的一个重要条件，详细说明见下面。

假设 p(x) 是最后的稳态，那么 detailed balance 可以用公式表示为：

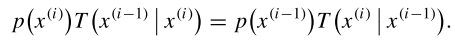
什么意思呢？假设上面状态图 x1 有 0.22 元， x2 有 0.41 元，x3 有 0.37 元，那么 0.22×1 表示 x1 需要给 x2 钱，以此类推，手动计算，可以发现下一个状态每个人手中的钱都没有变。值得说明的是，这里体现了一个很重要的特性，那就是从一个高概率状态 xi 向一个低概率状态 x(i-1) 转移的概率等于从这个低概率状态向高概率状态转移的概率（reversible，至于要不要转移又是另外一回事)。当然，在上面一个例子中，情况比较特殊，等号两边其实都是同一个东西。马氏链的收敛性质主要由转移矩阵决定, 所以基于马氏链做采样的关键问题是如何构造转移矩阵,使得平稳分布恰好是我们要的分布p(x)。但是考虑一维的情况，假设 p(x) 是一维高斯分布，x 是根据 markov chain 得到的一个样本，依照上面的等式，那么我们可以根据转移矩阵 T左 和 T右 （这里实际是 proposal distribution）来得到 p(xi) 和 p(x(i-1)) 的比率，进而按照一定的概率对这两个样本进行选择。通过大量这样的处理，得到样本就符合原始的 p(x) 分布了。这就是 MH 算法的基本原理。

4.2 Metropolis-Hastings Algorithm

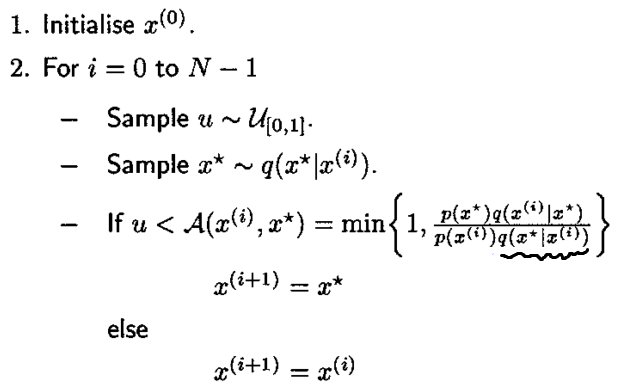
举个例子，我们要用 MH 算法对标准高斯分布进行采样，转移函数(对称)是方差为 0.05 的高斯矩阵，上述算法过程如下：

• 选取一个随机点 x0，作为一个采样点
• 以 x0 为中心，以转移函数为分布采取随机点 x1
• 以算法中的 A 概率接受 x1, 否则接受 x0
• 重复第二步第三步

注意到高斯分布是一个径向基函数，上面算法画波浪线的部分相等。

matlab 代码如下：

n = 250000;
x = zeros(n, 1);
x(1) = 0.5;
for i = 1: n-1
    x_c = normrnd(x(1), 0.05);
    if rand < min(1, normpdf(x_c)/normpdf(x(i)))
        x(i+1) = x_c;
    else
        x(i+1) = x(i);
    end
end

MH 算法中的 proposal distribution q(x) 也是需要小心确定的，详细知识可以查阅这篇介绍论文 (An introduction to MCMC for machine learning, Andrieu, Christophe). 可以看到，这个算法和模拟退火算法的思想是非常相似的，但是在模拟退火算法过程中，随着时间的增加，接受值大的区域的概率越来越高，直到找到最高点。

4.3 Gibbs Sampling

Gibbs Sampling 实际上是 MH 算法的一个变种。具体思路如下：假设在一定温度下一定量的分子在容器里做无规则的热运动，如何统计系统的能量呢？同样，我们用 Monte Carlo 的思想进行统计计算。我们假设所有的分子静止在某一个时刻，这是初识状态。固定其他的分子，根据分子间的作用力对其中一个分子进行移动，也就是说在该分子以一定的概率移动到领域的某一个地方，移动完了之后再静止。然后基于移动后的状态对下一个分子进行同样的移动操作...直到所有的分子移动完毕，那么现在的状态就是 Monte Carlo 采样的第二个样本。依照这样的顺序采样下去，我们对于这个系统就能计算一个统计意义上的能量了。从条件分布的角度来看，算法过程如下：

总体来讲，Gibbs Sampling 就是从条件概率中选择一个变量（分子），然后对该变量（分子）进行采样。当所有变量采样完毕之后，就得到了后面的一个状态，从而完成了对系统配置的采样。在 deep learning 的 RBM 中，gibbs 采样是已知权重参数和一个 v 变量，通过采样得到 h。通过 h 采样又可以得到另一个 v ，如此交替采样，就可以逐渐收敛于联合分布了。

Gibbs.py (对高斯分布进行 Gibbs 采样)

# -*- coding=utf8 -*-

# Code from Chapter 14 of Machine Learning: An Algorithmic Perspective
# A simple Gibbs sampler

from pylab import *
from numpy import *

def pXgivenY(y,m1,m2,s1,s2):
    return random.normal(m1 + (y-m2)/s2,s1)

def pYgivenX(x,m1,m2,s1,s2):
    return random.normal(m2 + (x-m1)/s1,s2)

def gibbs(N=5000):
    k=20
    x0 = zeros(N,dtype=float)
    m1 = 10
    m2 = 20
    s1 = 2
    s2 = 3
    for i in range(N):
        y = random.rand(1)
        # 每次采样需要迭代 k 次
        for j in range(k):
            x = pXgivenY(y,m1,m2,s1,s2)
            y = pYgivenX(x,m1,m2,s1,s2)
        x0[i] = x
    
    return x0

def f(x):
    return exp(-(x-10)**2/10)

# 画图
N=10000
s=gibbs(N)
x1 = arange(0,17,1)
hist(s,bins=x1,fc='k')
x1 = arange(0,17, 0.1)
px1 = zeros(len(x1))
for i in range(len(x1)):
    px1[i] = f(x1[i])
plot(x1, px1*N*10/sum(px1), color='k',linewidth=3)

show()

ps:

modified in 2013.11.1: 偶然发现统计之都有一篇类似的博客，gibbs采样解释得更加详细更加恰当，^_^，请点击这里

---

参考文献：

[1] PRML, chapter 11

[2] An introduction to MCMC for machine learning, Andrieu, Christophe

[3] 随机模拟的基本思想和常用采样方法（sampling）

[4] youtube 上的讲解 MCMC 的视频