在开始动态规划的讨论之前,先考虑一下斐波那契数列。
1、1、2、3、5、8、13、21·······
如何求解第20个数。计算斐波那契数列的一个最基本的算法就是根据定义进行求解计算:
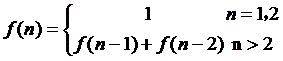
于是,求解代码如下:
public static long fib(int n){ if(n==1||n==2){ return 1; }else{ return fib(n-1)+fib(n-2); } }
求解第20个数:
1 fib(5)
2 fib(4) + fib(3)
3 (fib(3) + fib(2)) + (fib(2) + fib(1))
4 ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
5 (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
6 ............
没错,求解第20个数是足够用了,但是如果求解第1000个呢?
当用这种方法去求解第10000个数时,会出现如下的错误:
Exception in thread "main" java.lang.StackOverflowError
StackOverflowError为什么会有这样的错误?别忘了,我们使用的是递归的方式,递归栈不停的存储临时变量,当递归深度不停的增加时,会给栈带来沉重的计算负担,同时也导致计算性能的骤降。当然,聪明的程序员在递归次数超过一定次数时,就会避免这种方法。
所以,此时应该用更加优秀的方法去求解该问题。
在根据上面的代码段中,递归栈要不停的保存和计算上一个递归步骤中已经保存和计算过的值,造成递归栈的沉重负担和计算性能的下降。当然,可以通过设置栈的大小来避免栈溢出的异常,然后等上一段时间得出计算结果,但是这不是解决问题的最优方法。因为,应该有更好的解决方法。
重复计算和临时变量是上述问题的根本症结所在,如果解决了这个问题,是不是就可以在此基础上更进一步,找出更好的解决方法,答案是肯定的。
既然当前的计算需要用到上一步递归的计算结果,重复计算,那为什么不存储已经计算过的结果呢?将计算的结果存储在一个数组中,那么计算下一个斐波那契数就只需要它的前两个数相加即可。
初始化:将数组的前两个初始化为1;
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
初始化 |
|
1 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
1+1=2 |
|
1 |
1 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
1+2=3 |
|
1 |
1 |
2 |
3 |
5 |
0 |
0 |
0 |
0 |
2+3=5 |
|
1 |
1 |
2 |
3 |
5 |
8 |
0 |
0 |
0 |
3+5=8 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
0 |
0 |
8+5=13 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
0 |
13+8=21 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
13+21=34 |
代码如下:
private long[] fibs = new long[1000]; public void dynamicFib(){ fibs[0]=fibs[1]=1; for(int i=2;i<1000;i++){ fibs[i]=fibs[i-1]+fibs[i-2]; } }
那么fibs[999]就是第1000个斐波那契数。注意,这种方法也存在一定问题,那就是当求解的斐波那契数不断增大时,可能会出现类型溢出。这时候可以用BigInteger代替long。
所以运行代码之后第1000个斐波那契数是817770325994397771
动态规划[1]
第二个求解斐波那契数列使用的方式就是动态规划。它是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这里的这个表是我们在讨论斐波那契数列中的fibs数组。动态规划保存递归时的结果,因而不会在解决同样的问题时花费时间。所以速度比递归快。
状态转移方程[2]
动态规划中本阶段的状态往往是上一阶段状态和上一阶段决策的结果。如果给定了第K阶段的状态Sk以及决策UK(Sk),则第K+1阶段的状态Sk+1也就完全确定。也就是说Sk+1与Sk,Uk之间存在一种明确的数量对应关系,记为Tk(Sk,Uk),即有Sk+1= Tk(Sk,UK)。 这种用函数表示前后阶段关系的方程,称为状态转移方程。
如何设计动态转移方程
首先你要确定这道题是否可以用动态规划来做,即它是否满足最优化原理和无后效性原则。如果是,就开始设计:
一、确定问题的决策对象
二、对决策对象划分阶段
三、对各阶段确定状态变量
四、根据状态变量确定费用函数和目标函数
五、建立各阶段的状态变量的转移方程,写出状态转移方程
六、编程实现
思想很简单,也很容易理解。但是要如何去运用就必须实际验证。
动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题,它们的结果都逐渐被计算并被保存,从简单的问题直到整个问题都被解决。因此,动态规划保存递归时的结果,因而不会在解决同样的问题时花费时间。
动态规划例子
例1、设有n件物品,每件价值记为Pi,每件体积记为Vi,用一个最大容积为Vmax的背包,求装入物品的最大价值。
求装入物品的最大价值,用一个数组f[i][j]表示取i件商品填充一个容积为j的背包的最大价值,显然问题的解就是f[n][Vmax].
很显然,当背包的体积为0或者装入0件商品时,那么f[i][j]=0;
如果,背包的容积小于要装的第i件物品的体积,那么f[i][j]=f[i-1][j];
如果,背包的容积大于等于要装入第i件物品的体积,那么就考虑装了i-1件物品的价值和能装入该物品的后背包的价值。综上所述,写出状态转移方程:
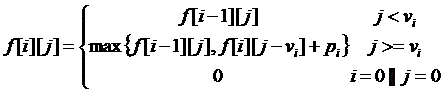
private int[] price = {4,5,6}; private int[] volum = {3,4,5}; private int[][] value = new int[4][11]; private int vmax = 10; public void solution(){ for(int i=0;i<=3;i++){ for(int j=0;j<=10;j++){ if(i==0||j==0){ value[i][j]=0; }else if(j<volum[i-1]){ value[i][j]=value[i-1][j]; }else if(j>=volum[i-1]){ value[i][j]=(value[i-1][j] > (value[i][j-volum[i-1]]+price[i-1]) ? value[i-1][j]: (value[i][j-volum[i-1]]+price[i-1])); } } } }
对于该问题的特例01背包(即每件物品最多放1件,否则不放人)问题,给出状态迁移方程:
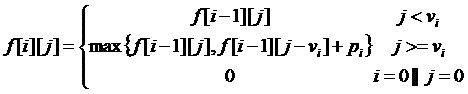
例2、给出一个整数序列S,其中有N个数,定义其中一个非空连续子序列T中所有数的和为T的“序列和”。对于S的所有非空连续子序列T,求最大的序列和。
首先,给出最大序列求和的状态转移方程
public static long getMax(int[] arr) { long start, all; start = all = arr[0]; for (int n = 1; n < arr.length; n++) { start = max(arr[n], start + arr[n]); all = max(all, start); } return all; }
例子持续更新中~~~未完待续!!
PS.我开通了博客园博客,欢迎大家关注!
网址:http://www.cnblogs.com/danger/
参考文献:
[1]http://zh.wikipedia.org/wiki/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92
[2]http://baike.baidu.com/view/7322318.htm