一、网络流的定义:有向图G=(V,E)中,点集中有一源点S,一汇点T。且S入度为0,T出度为0。对于每条边edge,都有一权值函数c,表示其容量,一权值函数f,表示其实际流量。
满足对于任意一条边都有f(edge)<=c(edge)。
二、最大流的定义:在不违背网络流的定义下,S到T的最大流量。
三、増广路的思想。
我们先考虑一个网络流:红色数字表示实际流量,蓝色表示边的容量,黄色表示更优的流量。
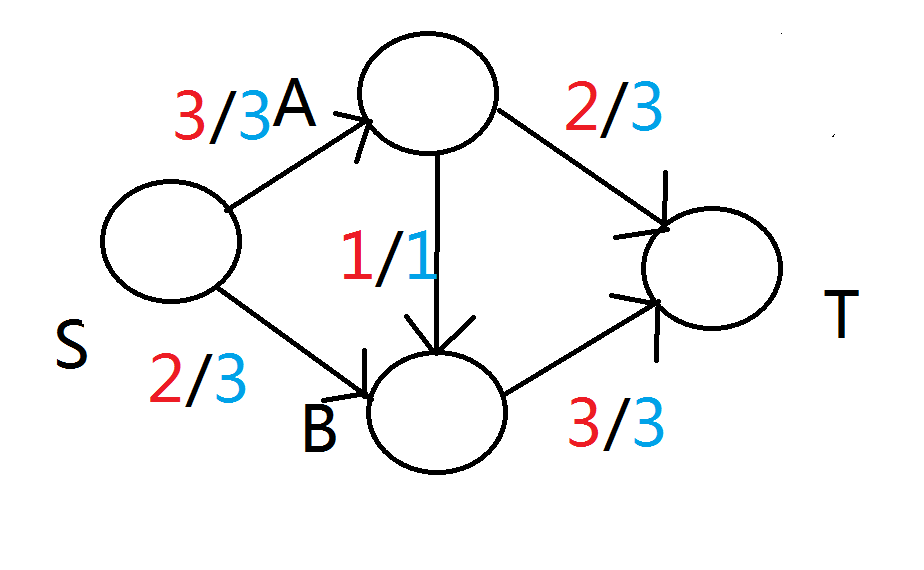 这个流从S到T的流量是5,但其显然不是最优的。
这个流从S到T的流量是5,但其显然不是最优的。
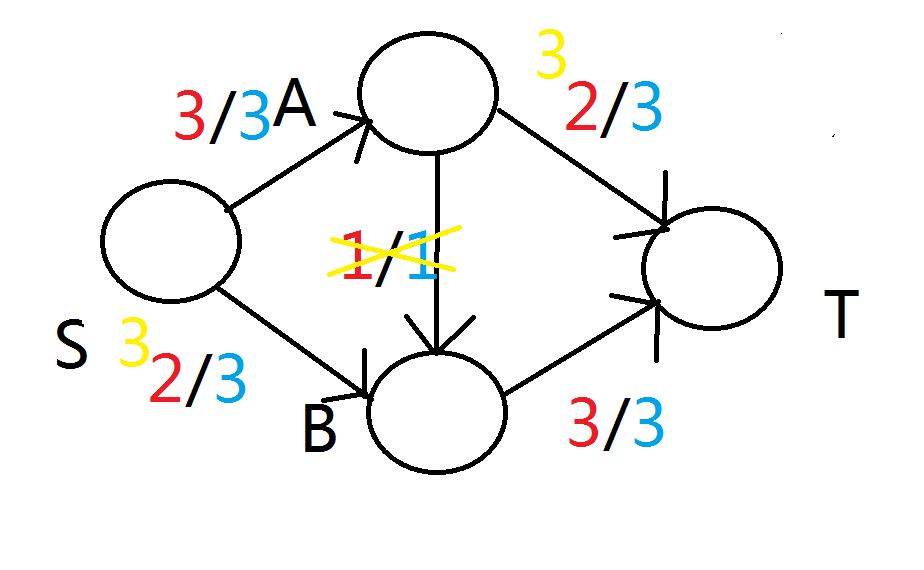 这个流比上面那个优,而且事实上,这个流就是当前网络的最大流。
这个流比上面那个优,而且事实上,这个流就是当前网络的最大流。
我们将两个图比较,得出下图
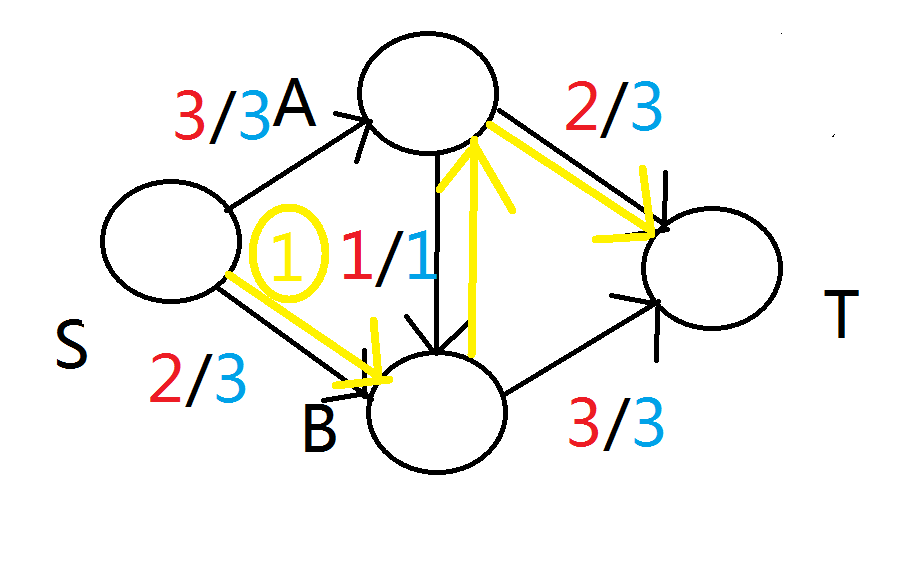 我们发现因为这条路径上的每条边流量都加了一。注意到其中有一条A到B的反向边,所以我们寻找这种路径时,应把原图中所有边的剩余流量和已经流量的反向边加进去(退流),当图中不存在这种路径时,此图已成最大流。(顺便提一下,这种路径叫増广路径)。
我们发现因为这条路径上的每条边流量都加了一。注意到其中有一条A到B的反向边,所以我们寻找这种路径时,应把原图中所有边的剩余流量和已经流量的反向边加进去(退流),当图中不存在这种路径时,此图已成最大流。(顺便提一下,这种路径叫増广路径)。
四、求最大流的算法:
FF:xyf大神说FF就是每次将源点的压力增加1,找一下増广路,慢点要死。于是直接上EK。
EK:每次找一条増广路,将这条路径上所有的流量增加(不管正向反向,其实这里已经没有流量这个概念了)找到增广路径中最小的△。
上代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<vector> #include<cstring> using namespace std; #define N 1100 #define INF 0x3F3F3F3F struct note { int to,cap,rev; }; vector<note> path[N]; bool used[N]; int n,m; void make_way(int u,int v,int c) { path[u].push_back((note){v,c,path[v].size()}); path[v].push_back((note){u,0,path[u].size()-1}); } int dfs(int s,int t,int f) { if(s==t) return f; used[s]=1; for(int i=0;i<path[s].size();i++) { note &tmp=path[s][i]; if(used[tmp.to]==false&&tmp.cap>0) { int d=dfs(tmp.to,t,min(f,tmp.cap)); if(d>0) { tmp.cap-=d; path[tmp.to][tmp.rev].cap+=d; return d; } } } return 0; } int max_flow(int s,int t) { int flow=0; while(1) { memset(used,0,sizeof(used)); int f=dfs(s,t,INF); if(f==0) return flow; flow+=f; } } int main() { scanf("%d %d",&m,&n); for(int i=1;i<=m;i++) { int u,v,c; scanf("%d %d %d",&u,&v,&c); make_way(u,v,c); } printf("%d ",max_flow(1,n)); }
dinic:就是先对图进行分层遍历,然后在分层图中进行dfs搜索,比EK快,10000的随即数据随便过。